Geometry Study Guide for the Math Basics

Circles

A circle is defined as the set of all points equidistant (the same distance) from a point called the center. That distance from the center is called the radius.

The distance across a circle through the center is called the diameter. Since the diameter is made up of two radii (the plural of radius), then \(d=2r\).

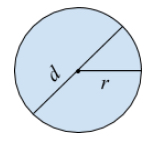
The perimeter of a circle is called the circumference. A very important mathematical constant called Pi (\(\pi\)) is defined as the ratio of the circumference to the diameter (\(\pi = \frac{C}{d}\)). This number is the same for every circle and it turns out to be the irrational number \(\pi = 3.14159…\). Usually, we rearrange the formula to find the circumference: \(C=\pi \cdot d\) or, because \(d=2r\), \(C = 2 \pi r\).

The area of the circle is found using the formula \(A = \pi \cdot r^2\).

For example, if a circle has a 3 cm radius, like this one, then:

\[C = 2\pi \cdot3\] \[6\pi \;cm\]

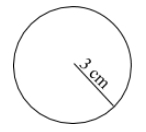
and

\[A=\pi \cdot 3^2\] \[9 \pi \; cm^2\]

Sometimes we use the decimal 3.14 as an approximation for \(\pi\), so:

\[C\approx 6 \cdot 3.14 \approx 18.84 cm\]

and

\[A \approx 9 \cdot 3.14 \approx 28.26 cm^2\]

Analyzing Figures

Some figures look quite similar to others, and some look like they might be able to be copied, twisted, and/or flipped to look like themselves.

Congruent

If two sides have the same length, we say they are congruent (\(\cong\)).
Likewise, if two angles have the same measure, they are congruent.

Two polygons are congruent if their corresponding sides and angles are congruent. Look at these two rectangles.

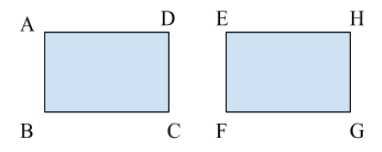
Within them, \(\angle{A}\) corresponds to \(\angle{E}\), \(\angle{B}\) corresponds to \(\angle{F}\), and so on. Likewise, \(\overline{AB}\) corresponds to \(\overline{EF}\), \(\overline{BC}\) corresponds to \(\overline{FG}\), and so on. All of the following are true:

\[\angle{A} \cong \angle{E} \\ \angle{B} \cong \angle{F} \\ \angle{C} \cong \angle{G} \\ \angle{D} \cong \angle{H} \\ \overline{AB} \cong \overline{EF} \\ \overline{BC} \cong \overline{FG} \\ \overline{CD} \cong \overline{GH} \\ \overline{DA} \cong \overline{HE} \\\]

So, we can say that \(ABCD \cong EFGH\).

Similar

If two polygons have the same number of sides and each corresponding angle is congruent, we say they are similar. We use the symbol \(\sim\) to show similarity. Look at the two figures.

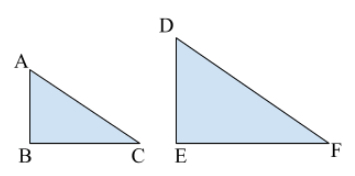
In this case \(\angle{A} \cong \angle{D}\), \(\angle{B} \cong \angle{E}\), and \(\angle{C} \cong \angle{F}\), so we say \(\triangle ABC \sim \triangle DEF\).

For similar polygons, the sides are proportional. For these triangles, that means \(\frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}\).

Symmetry

A figure has symmetry if it can be folded or rotated onto itself. There are two main types of symmetry.

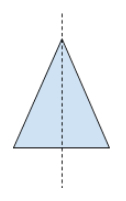
Line Symmetry (or fold symmetry) means a line exists where you can fold the figure exactly onto itself. This isosceles triangle has one line of symmetry.

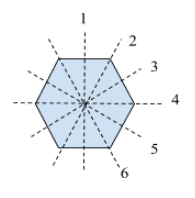
This regular hexagon has 6 lines of symmetry.

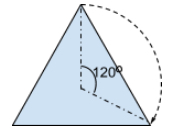
A figure has rotational symmetry if you can rotate the figure less than \(360^\circ\) onto itself. This equilateral triangle can be rotated \(120^\circ\) clockwise (or counterclockwise) onto itself.

Transformations

Figures can be manipulated by flipping, sliding, turning, or stretching. These are called transformations. If a transformation is performed, we call the initial figure the preimage and the final figure the image.

Reflection

A reflection is the result of flipping a figure over a line. In this case, the preimage \(\triangle{ABC}\) has been reflected over the y-axis onto the image \(\triangle{A’B’C’}\).

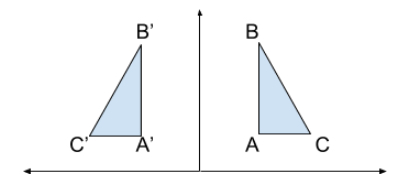
Note, it is common practice to label the vertices of the image as the primes of the vertices of the preimage. The point \(A\) has been reflected onto \(A’\) (A prime), for example.

Translation

A translation is the result of sliding a figure. In this case, the preimage \(\triangle{P}\) has been translated up and to the right onto its image, \(\triangle{P’}\).

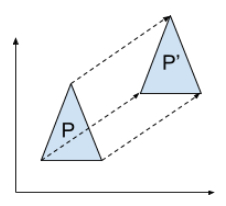
Rotation

A rotation is the result of turning an object around a point called the center of rotation. In this case, trapezoid \(H\) has been rotated \(90^\circ\) clockwise about the origin onto trapezoid \(H’\).

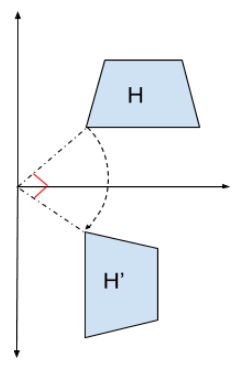
Dilation

A dilation occurs when a figure is stretched or compressed by an amount called the scale factor. In this case, the hexagon has been dilated by a scale factor of \(1.5\), meaning each side of the image is one and a half times bigger than its corresponding side of the preimage.