Advanced Basics Study Guide for the Math Basics

How to Prepare for the More Advanced Concepts on a Basic Math Test

General Information

There are a few concepts that don’t generally fall under the “basic” math skills category, but you may see them if you study math up through the end of Algebra I, so we thought we’d give you a little info on them. You’ll have to seek additional study and practice to be totally fluent in these skills, but this study guide should give you some background knowledge concerning them. At least you’ll know what those teachers and books are talking about!

Perplexing Polynomials

Algebra 2 continues the use of polynomials. The difference from Algebra I is, the polynomials typically have a degree of 2 or higher. But fear of the unknown aside, polynomials really aren’t that perplexing.

What is a Polynomial?

A polynomial is an algebraic expression that is defined for all real numbers. While a polynomial can have only one term, called a monomial, the prefix poly means many, so a polynomial usually has more than one term. Linear expressions like $3x-7$ as well as expressions like $3x^2+6x-5$ and $5x^7-4x^4+3x-1$ are examples of polynomials.

Working with Polynomials

We can combine polynomials by adding or subtracting like terms in the polynomial expressions, For example,

\[(3x^2-5x+6)+(4x^3-8x^2+9)\] \[4x^3+(3x^2-8x^2)-5x+(6+9)\] \[4x^3+(-5x^2)-5x + 15\] \[4x^3-5x^2-5x+15\]

Note: polynomials are generally written in descending order, meaning the value of the exponents decrease from left to right.

To multiply two polynomials, multiply each term in the first polynomial by each term in the second polynomial. This is simply an exercise in distribution. Finally, group and combine like terms. For example,

\[(2x^2-4x+1)(x^2-3x+5)\] \[2x^2(x^2-3x+5)-4x(x^2-3x+5)+1(x^2-3x+5)\] \[2x^4-6x^3+10x^2-4x^3+12x^2-20x+x^2-3x+5\] \[2x^4+(-6x^3-4x^3)+(10x^2+12x^2+x^2) +(-20x-3x)+5\] \[2x^4-10x^3+23x^3-23x+5\]

Note: when multiplying a tri nomial by another tri nomial, (3 terms by 3 terms), you should have 9 terms ($3\cdot 3$) before combining like terms. Use this trick to keep organized.

Dividing polynomials using long division is similar to long division with numbers. We may also be able to divide polynomials using factoring methods described in the Factoring Polynomial section, below. However, it’s helpful to know how to divide a polynomial by a linear binomial. Here’s an example using long division for reference.

\[\require{enclose} \begin{array}{r} 2x^2-x-3 \quad\quad\quad \\[-3pt] x+2 \enclose{longdiv}{2x^3+3x^2-5x-6} \\[-3pt] \underline{-(2x^3+4x^2)}\;\;\downarrow \phantom{-6}\;\; \\[-3pt] -x^2-5x \phantom{-6}\;\; \\[-3pt] \underline{-(-x^2-2x)}\;\;\downarrow \\[-3pt] -3x-6 \\[-3pt] \underline{-(-3x-6)} \\[-3pt] 0 \\[-3pt] \end{array}\]

So, $(2x^3+3x^2-5x-6) \div (x+2) = 2x^2-x-3$

Factoring Polynomials

It’s important to know that polynomials (especially the ones you’ll encounter in high school math) are generally products of two or more expressions. For instance, multiplying $x+1$ and $2x-3$ you get:

\[(x+1)(2x-3)=2x^2-3x+2x-3=2x^2-x-3\]

which is a quadratic trinomial (2nd degree polynomial with three terms).

To “factor (v)” a polynomial means to rewrite it as a product of its factors (n).
So, if the instructions were to factor $2x^2-x-3$, the response should be $(x+1)(2x-3)$. In other Math Basics sections, we cover methods of factoring these types of polynomials.

Now, in this advanced section, we need to learn how to deal with higher degree polynomials with more than three terms. The objective: find factors of the polynomial expression by finding possible rational roots of the polynomial function.

Let’s factor the polynomial from the section above:

\[2x^3+3x^2-5x-6\]

To do this, let’s look at roots of the polynomial function:

\[f(x)=2x^3+3x^2-5x-6\]

You can graph this on your calculator and look for roots or you can use the rational root theorem to factor the polynomial:

Look at all the factors of the last number ($6: 1,2,3,6$) and the first coefficient ($2: 1,2$).
Make a list of all the possibilities of the positive or negative factors of the last number divided by the factors of the first. $\pm(1,2,3,6,\frac{1}{2}, \frac{3}{2})$
Plug these values into the function and see if they’re zeros (roots).

\[f(1)=2(1)^3+3(1)^2-5(1)-6=-6\] \[f(-1)=2(-1)^3+3(-1)^2-5(-1)-6=0\] \[f(2)=2(2)^3+3(2)^2-5(2)-6=12\] \[f(-2)=2(-2)^3+3(-2)^2-5(-2)-6=0\] \[f(\frac{3}{2})=2(\frac{3}{2})^3+3(\frac{3}{2})^2-5(\frac{3}{2})-6=0\]

And so on. You’ll see that $x=-1$, $x=-2$, and $x=\frac{3}{2}$ are roots.

Then, do the following:

Turn the roots into linear factors by clearing fractions and getting zero on one side of the equation. $x=-1 \rightarrow x+1=0$, $x=-2 \rightarrow x+2=0$, and $x=\frac{3}{2} \rightarrow 2x-3=0$.
Rewrite the polynomial as a product of linear factors: $2x^3+3x^2-5x-6=(x+1)(x+2)(2x-3)$.

Now that we know how to factor, back to division. If you know how to factor a polynomial into its prime factors, division is as easy as canceling out common factors. So, the same division problem from above:

\[\dfrac{2x^3+3x^2-5x-6}{x+2}\]

can be rewritten as:

\[\dfrac{(x+1)(x+2)(2x-3)}{x+2}\]

Now, cancel:

\[\require{cancel}\] \[\dfrac{(x+1)\cancel{(x+2)}(2x-3)}{\cancel{x+2}}=(x+1)(2x-3)=2x^2-x-3\]

Fabulous Functions

You’ve been dealing with functions since before you even knew it. Geometric formulas, linear equations, and even many word problems are examples of functions.

What is a Function?

A function is a relation in which each domain element, x in the ordered pair is mapped with only one range element, y in the ordered pair.

For example, the relation ${(1, 1), (2, 3), (-3, 4), (5, 3)}$ is a function since any x maps to only one y. However, ${ (1, 2), (1, 5), (3, -5), (4, 7) }$ is not a function since the x value of 1 maps to two different y values: 2 and 5.

Uses of Functions

We can use functions to describe real-world phenomena. Functions help us determine an output if we know the input. Similarly, we can determine the input if we know the output.

For example, if your income A is a function of how many hours t and you are paid $15 per hour, then your income is a function defined by $A(t)=15t$.

Linear Functions

Linear functions are, at most, 1st-degree polynomials, for example:

\[y=3x+5\]

There is typically one solution for a linear function. The function $y=4$ is a linear function that has a degree of zero, since there is no x variable in the equation. We also call this function a constant function since it is defined by only a number. A constant function has infinitely many solutions.

Linear functions are usually simplified into the slope-intercept form, $y=mx+b$, where m is the slope and b is y-intercept for the graph of the line.

Investigating Inequalities

Linear inequalities are linear functions but y is greater than, less than, greater than or equal to, or less than or equal to $mx+b$.

Linear inequalities usually have infinitely many solutions. For example, if $x = 1$ for $y\gt x+4$, then $y=5,6,7,...$

The solution should be stated as a set of points that make the inequality true; ${ (1, 5), (1,6), (1, 7), …}$(.)

Uses of Inequalities

Linear inequalities can be used to tell us what the maximum or minimum values can be for a given situation. For example, if the number of leaves $y$ on a tree has to be at least the the sum of 20 and 15 times the number of branches $x$ then, $\ge 15x+20$ tells us at least how many leaves are on the tree given $x$ number of branches.

Graphing Inequalities

Let’s graph $y\gt \dfrac{1}{2}x + 1$ using the following steps:

Graph the line $y=\dfrac{1}{2}x + 1$. Draw the line dashed since the points on the line are not part of the solution. Draw a solid line if the inequality included $\ge$ or $\le$.
The line divides the coordinate plane into two half-planes.
Choose a point in either of the half-planes (that is above the line or below the line).
If the chosen point satisfies the inequality, then all of the points in that half-plane also satisfies the inequality. Show this by shading in the half-plane that contains the chosen point.

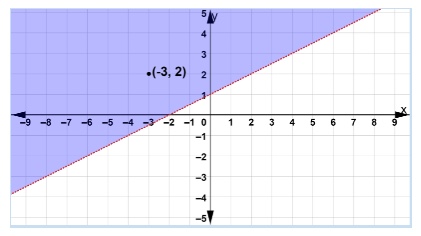
After showing $y=\dfrac{1}{2}x+1$ as a dashed line, we choose the point $(-3, 2)$ to substitute into the inequality to get:

\[2\gt \dfrac{1}{2}(-3)+2\] \[2 \gt \dfrac{-3}{2} + 2\] \[2\gt \dfrac{1}{2}\]

which is a true statement, so we shade above the line to complete the solution set for the inequality.

Alternatively, you can shade the solution set if the inequality sign is greater than and below the line if the inequality sign is less than.