Fractions, Decimals, and Percents Study Guide for the Math Basics
Page 1
How to Prepare for the Fraction, Decimal, and Percent Questions on a Math Test
General Information
Before you tackle this section, make sure you’ve mastered all of the concepts in our Numbers and Operations study guide and are successful with the accompanying practice questions and flashcards. You’ll be relying on those skills as you navigate the topics in this study guide. It will take you further into working with numbers, many of which are not whole. Many of the rules are the same, but there are some differences and added features.
Fractions
Are you one of the many people who think, “I was fine with math until fractions came along”? Ok, sure, there are a few rules when adding and subtracting. But with a little patience, a deep breath or two, and this study guide, you’ll soon realize that fractions aren’t scary at all. In fact, you probably already understand them more than you give yourself credit for. Clearly, you know what it means to share half of a candy bar with someone. Certainly, you understand the concept of quarters and how four of them make up a dollar. So don’t sell yourself short. You can do this!
Fraction Terms
So what is a fraction? Simply put, a fraction is just a part of a whole.
Half (or \(\frac{1}{2}\)) of a candy bar means that if the whole candy bar is two equal pieces (the bottom part of the fraction), then you have just one of those pieces (the top part of the fraction).
A monetary quarter (or \(\frac{1}{4}\)) means that if one dollar was divided into four equal pieces (again, the bottom part of the fraction), you’d have just one of those pieces (the top part).
But we don’t just call them the bottom part or the top part. We have words for those and it’s important to be comfortable with the terminology in order to master fractions.
Denominator— The denominator is the bottom part of the fraction. To remember, you might think Denominator means Down. This corresponds to how many equal parts make up the whole thing. In \(\frac{3}{8}\), for example, \(8\) is the denominator. That means that whatever item is being talked about (a candy bar, a dollar, or a day) is split up into 8 equal parts.
\[\begin{array}{|c|} \hline \\ {\;\;\;\; \text{ One whole candy bar }\;\;\;\;\;} \\ \hline \end{array}\]Here’s that same candy bar being split into 8 equal parts:
\[\begin{array}{|c|c|c|c|c|c|c|c|} \hline \\ {\;\;\;}&{\;\;}&{\;\;}&{\;\;}&{\;\;}&{\;\;}&{\;\;}&{\;\;\;} \\ \hline \end{array}\]When reading a fraction, the denominator is followed by “th(s)” with 2 and 3 as the exception.
\[\begin{array}{|c|c|} \hline {\textbf{Denominator}} & {\textbf{Words}} \\ \hline {2} & {\text{half or halves}} \\ \hline {3} & {\text{third(s)}} \\ \hline {4} & {\text{fourth(s)}} \\ \hline {5} & {\text{fifth(s)}} \\ \hline {...} & {etc.} \\ \hline \end{array}\]Numerator— The numerator is the top part of the fraction. For the fraction above, \(\frac{3}{8}, \; 3\) is the numerator. This value corresponds to the number of parts represented or counted.
Here’s a candy bar.

Here’s \(\frac{3}{8}\) of a candy bar (represented by the blue parts):
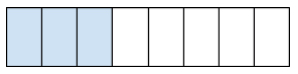
When reading a fraction, read the numerator and then the denominator. Here are some examples:
\(\frac{1}{5}\) = “one fifth”
\(\frac{2}{3}\) = “two thirds”
\(\frac{9}{13}\) = “nine thirteenths”
Improper fraction— An improper fraction means that the numerator is larger than the denominator, like \(\frac{11}{8}\). As fractions have been explained this doesn’t logically make sense. If a whole candy bar has been split into 8 pieces, how can I have 11 of them? For this reason, we can also represent these types of fractions as mixed numbers.
Mixed number— A mixed number is simply just a combination of whole items and a fraction. \(1 \frac{3}{8}\) is a mixed number read “one and three eighths”. You might use this number to tell about having one whole candy bar and \(\frac{3}{8}\) of another one.
Other Fraction Concepts
Now that we know how to talk about fractions, let’s delve a little deeper.
Equivalent Fractions—Here are three diagrams showing \(\frac{1}{2}\), \(\frac{2}{4}\), and \(\frac{4}{8}\) of a candy bar.
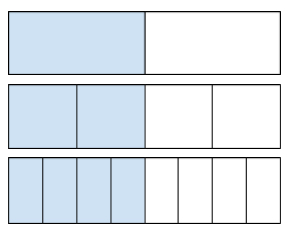
It’s pretty easy to see that all three fractions represent the same amount. For this reason, \(\frac{1}{2}\), \(\frac{2}{4}\), and \(\frac{4}{8}\) are equivalent fractions.
Fractions are equivalent if they have the same simplest form (see below).
Reducing/Simplifying Fractions—To simplify or reduce a fraction, you need to divide both the numerator and the denominator by their Greatest Common Factor (GCF). For \(\frac{8}{12}\) the \(GCF(8, 12) = 4\), so:
\[\frac{8 \div 4}{12 \div 4} = \frac{2}{3}\]For the example of \(\frac{2}{4}\) and \(\frac{4}{8}\) above, they both simplify to \(\dfrac{1}{2}\):
\(\dfrac{2 \div 2}{4 \div 2} = \dfrac {1}{2}\)
\(\dfrac{4 \div 4}{8 \div 4} = \dfrac {1}{2}\)
Changing an Improper Fraction to a Proper Fraction—Some multiple choice test give answer choices only as improper fractions, while others give choices as mixed numbers. For open ended questions, it’s important to read directions carefully to see which form is required.
To change from an improper fraction to a proper fraction, simply do long division. The remainder will be the numerator of the fractional part.
Write \(\frac{23}{5}\) as a mixed number.
\[\require{enclose} \begin{array}{r} 4 \\[-3pt] 5 \enclose{longdiv}{23} \\[-3pt] \underline{-20}\\[-3pt] 3 \\[-3pt] \end{array}\]So, \(\frac{23}{5} = 4 \frac{3}{5}\)
To go in the other direction (from mixed number to improper fraction), multiply the whole number by the denominator and add the numerator to the product.
Write \(5 \frac{1}{4}\) as an improper fraction.
\(4 \cdot 5 + 1 = 20 + 1 = 21\), so \(5 \frac{1}{4} = \frac {21}{4}\)
All Study Guides for the Math Basics are now available as downloadable PDFs