Geometry Study Guide for the Math Basics

Angles

When two lines intersect, four angles are formed. An angle is made up of two rays sharing a common starting point called the vertex. To name an angle, use the symbol \(\angle\) followed by the vertex or three points: ray, vertex, ray. This angle can be called \(\angle{B}\), \(\angle{ABC}\), or \(\angle{CBA}\).

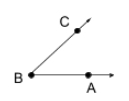
Note: It cannot be called \(\angle{CAB}\) because that would mean that point A is the vertex.

Measuring Angles

Use a protractor to measure an angle. Start by placing the little circle on your protractor directly on the vertex of the angle. Line up one of the rays on the bottom line of the protractor. If that ray is pointing to the right, use the numbers on the inside of the circle to tell you the measure of the angle.

This angle measures \(45^\circ\).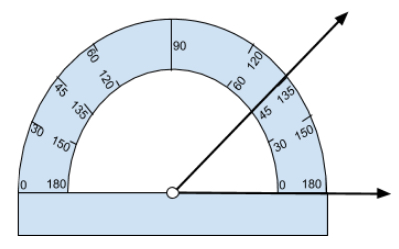

This angle measures \(120^\circ\).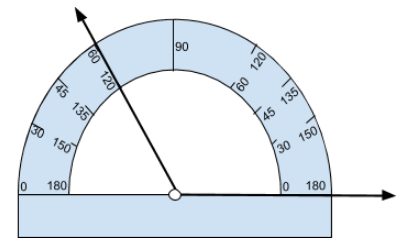

If the bottom ray is pointing to the left, use the numbers on the outside of the protractor to tell you the measure of the angle.

This angle measures \(30^\circ\).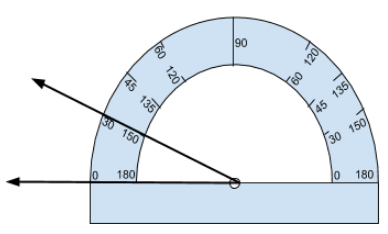

Types of Angles

An acute angle is an angle which measures less than \(90^\circ\).

Example: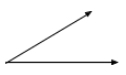

A right angle measures exactly \(90^\circ\). In pictures, you know an angle is right if it has this symbol:

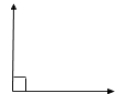
An obtuse angle measures between \(90^\circ\) and \(180^\circ\).

Example: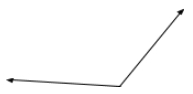

A straight angle measures exactly \(180^\circ\).

Example: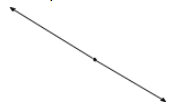

Angle Relationships

Two angles are complementary if their measures add up to \(90^\circ\).

Example: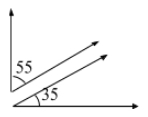

Two angles are supplementary if their measures add up to \(180^\circ\).

Example: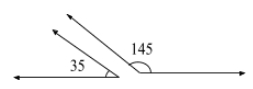

Triangles

Triangles are the most basic plane figure. Every other plane figure can be split into triangles. Because of this, we’ve not only developed many names for types of triangles, but we’ve also created a whole new branch of mathematics for the study of triangles (trigonometry).

Types of Triangles

A triangle is acute if all three angles are acute.

Examples: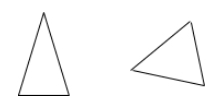

It is right if one angle measures \(90^\circ\).

Examples: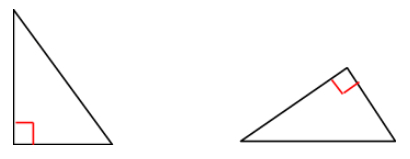

We call a triangle obtuse if one angle is obtuse.

Example: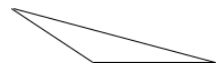

For right triangles, the side opposite the right angle is called the hypotenuse. The remaining two sides are called legs.

Example: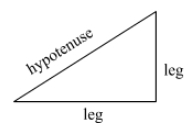

If all sides (and angles) are congruent, we call the triangle equilateral.

Example:

If exactly two sides are congruent, we say it’s an isosceles triangle.

Examples: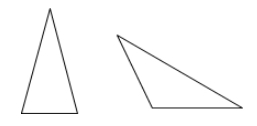

Otherwise (no sides congruent), the triangle is scalene.

Examples: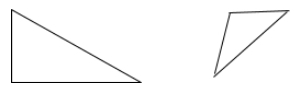

Pythagorean Theorem

The pythagorean theorem is a special property only to be used for right triangles. It states that if a right triangle has legs \(a\) and \(b\) and hypotenuse \(c\), then \(a^2 + b^2 = c^2\).

Often, we use the pythagorean theorem to find a missing side of a triangle. Find the missing side of the following right triangle.

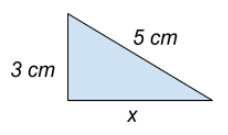
The legs are \(3\) and \(x\), and the hypotenuse is \(5\), so
\(3^2 + x^2 =5^2 \\ 9 + x^2 = 25 \\ x^2 = 16 \\ \sqrt{\mathstrut{x^2}} = \sqrt{16} \\ x = 4\;cm\)