Advanced Basics Study Guide for the Math Basics

Applying Absolutes

The absolute value of a value, a, measures the distance that a is from 0, either from the left or the right side of 0 on a number line. Since the absolute value measures distance, its value will never be negative. If we wanted to choose numbers that are three units from 0, we would choose \(-3\), the left sided distance and \(3\), the right sided distance. So, \(\vert -3 \vert = 3\) and \(\vert 3 \vert = 3\)

Absolute value equations parallel this fact. An absolute value equation in the form, \(\vert x+b \vert =c\) where \(b,c\) are constants is solved as follows:

\(x+b = c\) is the right sided distance

\(x+b=-c\) is the left sided distance

For example, solve \(\vert 2x + 8 \vert =24\):

\[2x+8 = 24 \text{ or } 2x + 8 = -24\] \[2x=16 \text{ or } 2x = -32\] \[x=8 \text{ or } x = -16\]

An absolute value inequality is similar. There are two types of these inequalities:

\(\vert x+b \vert \lt c\), then \(-c \lt x+b \lt c\) and solve the combined inequality for x \(\vert x+ b \vert \gt c\), then \(x+b \lt -c\) or \(x+b \gt c\) and solve the inequalities for x

The absolute inequality is solved with the same methods, whether the inequality signs are \(\ge\) or \(\le\).

For example, solve \(\vert 3x + 9 \vert \lt 18\):

\[-18 \lt 3x+ 9 \lt 18\] \[-27 \lt 3x \lt 9\] \[-9 \lt x \lt 3\]

Subduing Systems of Equations

A system of equations is typically used to find a solution for a problem that involves 2 unknowns different constraints. They involve a set of equations that are both dealt with during the same procedure.

Using Systems of Equations

A system of equations involves 2 or more equations with the same variables used in each equation. The goal is to find the solution for the variables that solves each equation in the system.

For example, this problem involves a system of 2 equations with 2 different variables:

“If the sum of two numbers is 24 and their product is 140, what are the 2 numbers.”

The system of equations used to solve this problem would be:

\[x + y = 24\] \[x \cdot y = 140\]

Solving Systems of Equations

In most Algebra 2 courses, a system of equations involves 2 equations with 2 variables. We can solve the system several ways:

• Graph the equations in the system to see if there is a point of intersection.

• Substitution—Substitute the value for one equation into the other.

• Elimination—Use a process of eliminating one of the variables by combining the equations.

Method 1: Graphing

Let’s look at an example that involves graphing. Solve the system of equations graphically:

\[x+y=3\] \[-x+y=1\]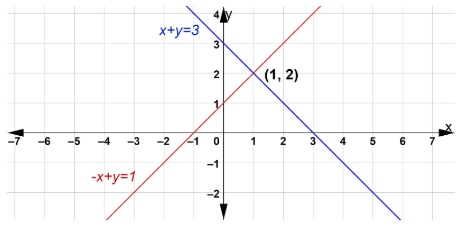

The graph shows the solution is the intersection point of the 2 lines at \((1, 2)\). Plugging \(x = 1\) and \(y = 2\) satisfies both equations. Since there is has only one solution (that is, one point of intersection), we say the solution is unique.

One of the problems with solving a system graphically occurs when the exact solution for the point of intersection is difficult to find. To remedy this, we can use the process of elimination to determine the exact solution.

Method 2: Elimination

Solve the following system by eliminating the x variable when combining the following system:

\[x+2y = 7\] \[3x-4y = -9\]

Multiply the 1st equation by \(-3\) before combining it with the 2nd equation to find the value for \(y\).

\[-3x-6y = -21\] \[\underline{+ 3x-4y=-9}\] \[\phantom{+3x}-10y = -30\]

So, \(y = 3\). Substituting the value for \(y\) into the 1st equation we have:

\[x+2(3) = 7\] \[x+6=7\] \[x=1\]

So the solution to the system is \((1, 3)\).

Method 3: Substitution

When using the substitution method to solve a system of equations, solve one of the equations for either \(x\) or \(y\) and substitute it into the other equation in order to find the value for one of the variables.

For example, use the substitution method to solve this system:

\[2x+y=8\] \[4x+2y=16\]

Solving the 1st equation for \(y\) and substituting its value into the 2nd equation we have:

\[y=-2x+8\]

then:

\[4x+ 2 (-2x+8)=16\]

Solving for \(x\):

\[4x-4x+16=16\] \[16=16\]

which, of course, is a true statement.

What this is telling us is there are infinitely many solutions for the system. Notice that the second equation is a multiple of the first. Whenever this occurs, there will always be an infinite number of points that lie on the graphs of either equation since the graphs are the same line. So, we can state our solution set as \((x, -2x+8)\) where \(x\) is any real number.

If the statement, like the one in the following example, were not true, then no solution exists and we say there is “no solution.”

To see this, solve the following system using the substitution method:

\[3x+y = 4\] \[3x+y = 10\]

Solving the 1st equation for \(y\) and substituting its value into the 2nd equation we have:

\[y=-3x+4\]

then

\[3x + (-3x + 4) = 16\]

Trying to solve for \(x\):

\[3x-3x + 4 = 16\] \[4=16\]

This is not a true statement. This time we are being told that there is no solution for the system. This is happening because the graphs of the 2 lines are parallel but with different y-intercepts, so they do not intersect.

Math with Matrices

In more advanced math courses, you will look at a different method for solving a system of equations: matrices. If you just use one, it will be called a matrix. The plural for matrix is matrices.

The Use of Matrices

To solve a system of linear equations, we can also work with only the coefficients and constants.

The system,

\[3x + 2y = 1\] \[4x - 5y = 4\]

reduces to

\[\begin{bmatrix} 3 & 2 & 1 \\ 4 & -5 & 4 \\ \end{bmatrix}\]

This array of numbers is a called a matrix and we typically use brackets to notate a matrix.

The Basics

A matrix contains rows (horizontal) of numbers as well as columns (vertical) of numbers. The dimensions of a matrix are how many rows and how many columns it has.

An m by n matrix, where m and n are Integers, will have m rows and n columns of numbers in its array. We note the dimensions as \(m \times n\). An element in a matrix, \(a_{m,n}\) is just one of the numbers in row m and column n in the array. In the \(4 \times 3\) matrix below, \(a_{2,4} = 9\) and \(a_{3,1} = 0\).

\[\begin{bmatrix} 3 & 2 & 1 & 6\\ 4 & -5 & 4 & 9 \\ 0 & 2 & -8 & 1 \\ \end{bmatrix}\]

We can combine matrices by adding or subtracting corresponding elements as long as the matrices have the same dimensions.

For example, let

\[A = \begin{bmatrix} 3 & 2 & 1\\ 4 & -5 & 4\\ \end{bmatrix} \text{, and } B = \begin{bmatrix} 1 & 0 & 6 \\ 5 & -2 & 8 \\ \end{bmatrix}\]

be 2 matrices.

\[A + B = \begin{bmatrix} 3+1 & 2+0 & 1+6 \\ 4+5 & -5 + -2 & 4+8 \\ \end{bmatrix} = \begin{bmatrix} 4 & 2 & 7 \\ 9 & -7 & 12 \\ \end{bmatrix}\]

Subtracting matrices works the same way, however the corresponding entries are being subtracted instead of added.

To multiply 2 matrices, the number of rows in the first matrix of the product must equal to the number of columns in the second matrix. An element in the product is the sum of the products of the corresponding elements in the rows in the 1st matrix and the elements in the columns in the 2nd matrix.

For example, let these be 2 matrices:

\[A = \begin{bmatrix} 3 & 2 & 1 \\ 4 & -5 & 4\\ \end{bmatrix} \text{, and } B= \begin{bmatrix} 1 & 2 \\ 3 & 5 \\ 0 & 6 \\ \end{bmatrix}\]

We can find \(AB\) since \(A\) has \(2\) rows and \(B\) has \(2\) columns. Now:

\[AB = \begin{bmatrix} (3 \cdot 1 + 2\cdot 3 + 1 \cdot 0) & (3 \cdot 2 + 2 \cdot 5 + 1 \cdot 6) \\ (4 \cdot 1 + -5 \cdot 3 + 4 \cdot 0) & (4 \cdot 2 + -5 \cdot 5 + 4 \cdot 6)\\ \end{bmatrix} = \begin{bmatrix} 9 & 22 \\ -11 & 7 \\ \end{bmatrix}\]

This arms you with enough knowledge to be able to use matrices to be able to solve linear systems in future Algebra courses.

Extreme Exponents

We have looked at exponents for expressions that are integers. Now let’s look at the exponents that are fractions, or rational exponents.

Rational Exponents

Exponents that are in the form \(a^\frac{m}{n}\), where \(m\) and \(n\) are Integers and \(a\) is a real number, is an expression with rational exponents. We can simplify these expressions by converting to radical form:

\[a^\frac{m}{n} = \sqrt[n]{a^m} \text{ or } (\sqrt[n]{a})^m\]

While it is possible to perform either \(m\) or \(n\) first, it is generally easier without the use of technology to find the \(n\)th root first, then take the \(m\) power second.

Simplifying, we have:

\[64 ^\frac{2}{3} = (\sqrt[3]{64})^2 = 4^2 =16\] \[32^\frac{6}{5} = (\sqrt[5]{32})^6 =2^6 =64\]

We can also simplify complicated radical expressions by converting them in rational from before simplifying.

Simplify the following we have,

\[\sqrt[3]{a^2} \cdot \sqrt[4]{a^3}\] \[a^\frac{2}{3} \cdot a^ \frac{3}{4}\] \[a^{\frac{2}{3} + \frac{3}{4}}\] \[a^\frac{17}{12}\] \[\sqrt[12]{a^{17}}\]

Another example:

\[\sqrt[2]{x^5} \cdot \dfrac{1}{(\sqrt[3]{x})^2}\] \[x^\frac{5}{2} \cdot x^{-\frac{2}{3}}\] \[x^{\frac{5}{2} - \frac{2}{3}}\] \[x^\frac{11}{6}\] \[\sqrt[6]{x^{11}}\]