Advanced Basics Study Guide for the Math Basics

A Quadratic Quest

Now we will look at 2nd degree polynomials which are also referred to as quadratics.

What is the Meaning of “Quadratic?”

Quadratic comes from the term quad which means to square, so the variable in the polynomial is squared. So the expression \(x^2+2x-5\) is a quadratic expression that has a degree of 2.

Quadratic Equations

A quadratic equation in the form \(ax^2 + bx + c =0\) where \(a, b, c\) are constants, is said to be in standard form.

There are several methods for solving a quadratic equation:

Completing the square
Factoring
Quadratic formula: \(x = \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}\)
Graphing

Each of these will find the roots of the quadratic equation.

Quadratic Inequalities

Similar to linear inequalities, quadratic inequalities usually have many solutions.

Let’s look at the steps involved in solving a quadratic inequality by factoring.

Solve \(x^2-2x-8 \le 0\)

Step 1: First set the quadratic equal to zero and solve for x to find the boundary points on the x-axis in order to determine the solution.

\[x^2-2x-8 = 0\] \[(x+2)(x-4)=0\] \[x+2 = 0 \text{ or } x-4 = 0\] \[x = -2 \text{ or } x = 4\]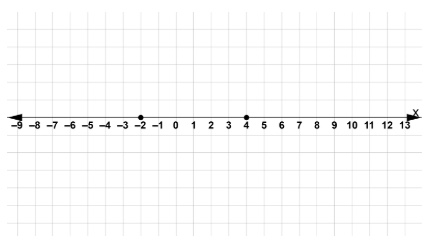

The points at \(-2\) and \(4\) divide the \(x\) axis into 3 segments.

Step 2: Choose an \(x\) value in each of the three segments to determine if the inequality is satisfied.

If \(x = -3\) then:

\[(-3)^2 -2(-3)-8 \lt 0\] \[9+6-8 \lt 0\] \[7 \lt 0 \text{ is not true}\]

If \(x = 0\) then:

\[(0)^2 -2(0) - 8 \lt 0\] \[-8 \lt 0 \text{ is true}\]

If \(x = 5\) then:

\[(5)^2 -2(5)-8 \lt 0\] \[25-10-8 \lt 0\] \[7 \lt 0 \text{ is not true}\]

Step 3: Since \(x = 0\) is the only value that makes the inequality true, we shade all numbers on the \(x\) axis between \(-2\) and \(4\), as in our solution set shown in red below.

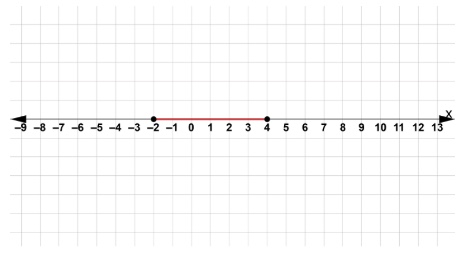
Stated algebraically, the solution set is \(-2 \le x \le 4\) or \([-2, 4]\) in interval notation.

Quadratic Functions

Examples of quadratic functions are:

\[f(x)=x^2-3x+2\] \[v(t) = -5t^2 + 3t -1\] \[H(a) = a^2 -2a\]

The standard form of a quadratic function is

\[f(x)=ax^2+bx +c\]

where \(a, b, c\) are constants.

There are many applications that involve quadratic functions. Revenue generated in selling a product can be stated in the form of a quadratic equation. For example:

Suppose that a company sells \(x\) number of calculators for a price of \(p\) dollars is represented by \(x = 45,000 - 375p\). The revenue, \(R\), generated is the product of the number of calculators sold and the price at which they are sold. Then:

\[R=xp\] \[R = (45,000 - 375p)p\] \[R(p) = -375p^2 + 45,000p\]

So, the revenue is a quadratic function that is written in terms of the price.

A quadratic function in vertex form is:

\[f(x) = a(x-h)^2 + k\]

where \((h, k)\) is the vertex of the graph of the function, and \(a\) is a vertical stretch of the graph if \(a \gt 1\) or a vertical compression if \(0 \lt a \lt 1\). Also if \(a \lt 0\), then the graph of \(f\) is reflected about the \(x\)-axis.

The Strange Cases of Non-Linear Graphs

There are a number of graphs that do not show a straight line and you may need to at least be able to recognize them. Here are some examples:

The graph of a quadratic function, called a parabola, is a U-shaped curve that has certain attributes you will need to know.

The parent function for the graph of a quadratic function is \(f(x)=x^2\). Its graph is shown below.

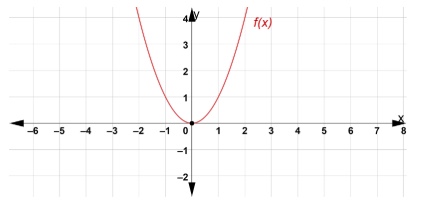
Notice the U shape curve for the graph. The vertex is at the origin and represents a turning point where the graph changes direction.

Now let’s look at using the vertex form to transform or move the graph of \(x^2\) around the plane. For example, the graph of \(f(x)=-(x-2)^2 + 3\) has its vertex at \((2, 3)\) and is reflected about the \(x\)-axis since \(a = -1\). The graph is shown below.

You will also need to be familiar with higher degree polynomials.

This one, \(f(x)=x^3\), a third-degree polynomial is graphed as an S-shaped curve, shown below.

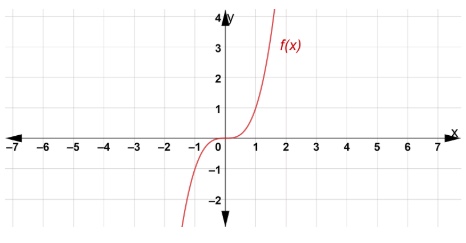
Like the parabola, its graph can also be transformed in the plane.

While not polynomials, you will need to be familiar with other classes of functions such as exponential and logarithmic functions.

Below is the graph of an exponential function \(f(x)=2^x\) and \(g(x) = log_{2}{x}\).

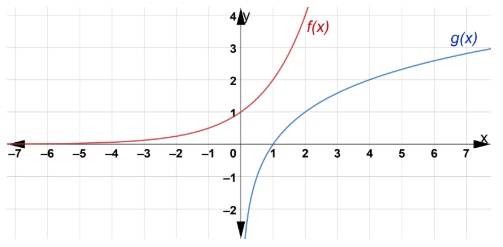
There is a relationship between these two graphs. They are inverses of each other, since reflecting one of the graphs about the line \(y = x\) produces the other graph as shown below.

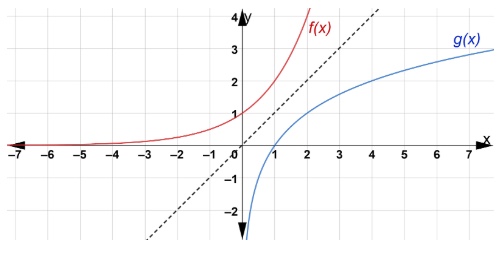
Again, like the parabola, these graphs can also be transformed in the plane.