Mathematics: Geometric and Spatial Reasoning Study Guide for the TSIA2
Page 5
Basic Trigonometry
In essence, trigonometry deals with triangle calculations. It is useful in surveying, navigation, astronomy, and other areas.
Angle Concepts
As we will see below, angles are treated a little more elaborately in trigonometry than they are in geometry.
Angle Measures
As defined earlier, a unit named radian is commonly used in trigonometry as an angle measure. In the diagram below, a radius length is wrapped around a circle to form an arc and two other radii are drawn from the circle’s center to the endpoints of the arc. The angle formed, \(\angle t\), has a measure of one radian. It’s about \(57.3^\circ\).
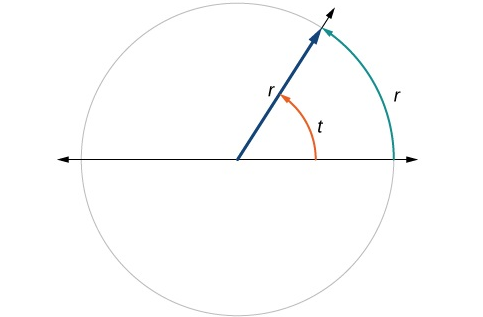
Retrieved from: https://openstax.org/books/algebra-and-trigonometry/pages/7-1-angles
Unlike degrees, when an angle measure is written in radians, there is no unit needed, So if you see \(\angle ABC=2\), that will mean \(2\) radians. Sometimes the word radians is written for clarity, but officially, it isn’t required. Very commonly you will see radian measures expressed in terms of \(\pi\).
To convert from degrees to radians, a good thing to know is that \(180^\circ = \pi\) radians. This relationship is handy for converting:
\[\dfrac{\text{Degrees}}{180^\circ} = \dfrac{\text{Radians}}{\pi}\]Example
Convert \(120^\circ\) to radians.
\[\dfrac{\text{Degrees}}{180^\circ} = \dfrac{\text{Radians}}{\pi}\] \[\dfrac{120^\circ}{180^\circ} = \dfrac{\text{radians}}{\pi}\] \[\text{radians} = \dfrac{120}{180} \pi\] \[\dfrac{2\pi}{3}\]Angle Position and Direction
In trigonometry, we encounter positive and negative angles. This stems from picturing an angle being generated from a standard position (one in which we imagine an angle having an initial side on the \(x-\) axis, and a terminal side rotated around \((0, 0)\) from the initial side).
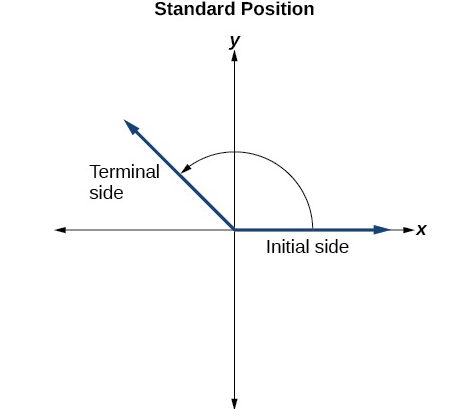
Retrieved from: https://openstax.org/books/algebra-and-trigonometry/pages/7-1-angles
If the terminal side has been rotated counterclockwise from the initial side, the angle is considered positive.
If the terminal side has been rotated clockwise from the initial side, the angle is considered negative.
It’s like a number line where one direction is positive and the other is negative.

Retrieved from: https://openstax.org/books/algebra-and-trigonometry/pages/7-1-angles
The diagram shows an angle in standard position that can be thought of as either a \(140^\circ\) angle or a \(-220^\circ\) angle. Angles like this that share a terminal side are called coterminal angles.
Trigonometric Functions
Trigonometric functions are functions of angles. The values of the functions can be defined in terms of ratios of sides in a right triangle.
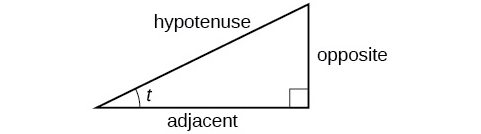
Retrieved from: https://openstax.org/books/algebra-and-trigonometry/pages/7-1-angles
The most used functions are the sine, cosine, and tangent. This table gives their ratios.
\[\begin{array}{ccc} \text{Name} & \text{Abbreviation} & \text{Ratio}\\ \hline \text{Sine of angle } t & \text{sin}(t) & \frac{\text{opposite leg}}{\text{hypotenuse}}\\ \text{Cosine of angle } t & \text{cos}(t) & \frac{\text{adjacent leg}}{\text{hypotenuse}}\\ \text{Tangent of angle } t & \text{tan}(t) & \frac{\text{opposite leg}}{\text{adjacent leg}}\\ \end{array}\]A common way to remember these ratios is the acronym SOHCAHTOA, which stands for Sine is Opposite over Hypotenuse, Cosine is Adjacent over Hypotenuse, Tangent is Opposite over Adjacent.
The two special triangles shown earlier can be used to find the exact values of sines, cosines, and tangents.
Example 1

What is the sine of the \(30^\circ\) angle?
\[\text{Sine} =\dfrac{\text{opposite leg}}{\text{hypotenuse}}\] \[\text{sin}(30^\circ) = \dfrac{x}{2x}\] \[\text{sin}(30^\circ) = \dfrac{1}{2}\]Example 2

What is the cosine of the \(45^\circ\) angle?
\[\text{Cosine}=\dfrac{\text{adjacent leg}}{\text{hypotenuse}}\] \[\text{cos}(30^\circ) = \dfrac{x}{x\sqrt{2}}\] \[\text{cos}(30^\circ) = \dfrac{1}{\sqrt{2}}\]Rationalize the denominator and get:
\[cos(30^\circ) = \dfrac{\sqrt{2}}{2}\]Solving Right Triangles
For most angles, exact values are not available, but calculators can supply values as accurate as you may need. That’s what we will use in this section.
Given One Side and One Acute Angle
If you have a right triangle in which you are given one side and one acute angle, you can find either of the other two sides using a trig ratio.
Calculate the length of the hypotenuse in this triangle.

From the point of view of the \(24^\circ\) angle, \(15\) is the opposite leg, and \(x\) is the hypotenuse. We will need to use the sine function in this problem.
\[\text{sin }24^\circ = \dfrac{15}{x}\] \[x = \dfrac{15}{\text{sin }24^\circ}\]Find sin \(24^\circ\) using a calculator.
\[x = \dfrac{15}{0.407}\] \[x=36.9\]Given Two Sides
If you have a right triangle in which you are given two sides, you can find either acute angle using a trig ratio.
Calculate the measure of \(\angle \text{B}\) to the nearest degree in this triangle.

From \(\angle\text{B’s }\) point of view, \(9\) is the opposite leg and \(15\) is the adjacent side. We will need to use the tangent function in this problem.
\[\text{tan } \angle \text{B} = \dfrac{9}{15}\] \[\text{tan } \angle \text{B} = 0.60\]Use a calculator to find the inverse tangent of \(0.60\):
\[\text{tan}^{-1}(0.60) = 31^\circ\]All Study Guides for the TSIA2 are now available as downloadable PDFs