Mathematics: Algebraic Reasoning Study Guide for the TSIA2
Page 1
General Information
Both of the TSIA2 tests, the CRC and the Diagnostic Test, contain a math section with questions covering these topics:
- Quantitative Reasoning
- Algebraic Reasoning
- Geometric and Spatial Reasoning
- Probabilistic and Statistical Reasoning
The skills tested are the same on both tests and you won’t know if you’ll need to take the Diagnostic Test until after you complete the CRC. So, it’s a great idea to go ahead and prepare as if you’ll need to take both of them.
On the CRC, you’ll find seven questions related to algebraic reasoning, whereas there will be 12 of them on the Diagnostic Test. You’ll find an outline of all of the algebra skills covered on both tests in this study guide, as well as some information about each. We also provide practice questions and flashcards to help you study, and encourage you to seek additional assistance for any problem areas. Be sure to also use our other three study guides for the TSIA2 Mathematics tests as you prepare.
The only question type on these math tests is multiple-choice.
Solving Equations and Inequalities
Keep in mind that the term solving means finding values that, when substituted for variables, make the statement (equation or inequality) true. The procedures are similar for both equations and inequalities, with the exception of multiplying or dividing both sides by a negative number. In an inequality, these operations require you to change the direction of the inequality sign.
Linear Equations
Linear equations result in a straight line when they are graphed. Linear equations can be written in several forms, and can be converted from one form to another with algebra. One common form is \(y=mx + b\), where b is the y-intercept (value of y where the line crosses the y-axis) and m is the slope of the line (how much the y value changes for a given change in x). Other forms reveal other characteristics of the line.
Word Problems and Linear Equations
Many real-life situations can be described with linear models. Often, the information given in a problem can be used to form an equation that describes the situation. This is the model. Usually, the equation can be solved to find the required solution.
For example, suppose a car is traveling at a rate of \(50\) miles per hour. How long does it take to travel \(120\) miles?
If \(y\) is miles traveled, and \(x\) is the hours traveled, then the model is:
\[y = 50x\]In this case we know that \(y\) is 120 miles, so:
\[120 = 50x\]To solve for \(x\), we have to divide both sides by 50, so:
\[x = 120 \div 50\]or \(2.4\) hours.
General Solving Procedure
Solving an equation for a variable means to find an equivalent equation with that variable alone on one side. Do this by adding, subtracting, multiplying, or dividing both sides of the equation by the same quantity.
Example
Solve \(4x + 2y = 8\) for \(y\):
\[4x + 2y = 8\]subtract 4x from both sides
\[2y = 8 - 4x\]divide both sides by 2
\[y = 4 - 2x\]re-order to put it in the form \(y \;=mx \;+\; b\)
\[y = -2x + 4\]Inequalities
An inequality is a statement of comparison between quantities that is not an equality. There are four possible ways to state an inequality.
\(a<b\) \(\quad a\) is less than \(b\).
\[5<11 \text{ is true.}\]\(a>b\) \(\quad a\) is greater than \(b\)
\[11>5 \text{ is true.}\]\(a\leq b\) \(\quad a\) is less than or equal to \(b\)
\[3 \leq 6 \text{ is true, and so is } 3 \leq 3 .\]\(a\geq b\) \(\quad a\) is greater than or equal to \(b\)
\[8 \geq 6 \text{ is true, and so is } 8 \geq 8 .\]General Procedure
Solving linear inequalities is very similar to solving equalities. There is one important change. As mentioned before, if you multiply or divide by a negative number, the direction of the inequality sign must be reversed.
Example
Consider the following linear inequality:
\[-3y - 1 \ge 2x + 2\]To solve, begin by isolating y:
\[-3y \ge 2x + 3\]and dividing both sides by \(-3\), remembering to switch the direction of the inequality:
\[y \le -\frac{2}{3}x - 1\]which graphs as:
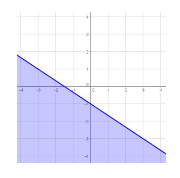
Graphically, the linear inequality is a bold line (because the inequality is less than/greater than or equal to, so the points along the line are also included in the solution set), with all values below and along the line shaded. All of these points are shaded because, when plugged into the original inequality, they yield true statements; consequently, they make up the solution set.
Systems of Linear Equations
A set of linear equations where the number of equations matches the number of variables is a linear system of equations. A value of (x,y) that works in both equations is the solution of the system. This is the spot where the lines intersect. If the lines are parallel, there are no solutions. In the rare case where both equations have the same graph, there are infinitely many solutions.
General Procedure
Finding a solution to the system of equations can be done as shown below. Graphing the two equations is helpful for visualizing the solution, but it can be a bit time-consuming, and can involve estimating a result.
Substitution and elimination are often the preferred ways to solve systems of linear equations.
Example
Consider the following system of linear equations:
\(-x + y = 1\), and
\(2x + y = 4\), which graphs as:
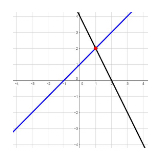
The point, \((1,2)\), marked in red, indicates the solution to the system of equations. It is the point that lies along both lines and marks their intersection.
Here are two methods for solving systems of equations:
Substitution
The system \(x + y = 5\) and \(x - 2y = 2\) will be solved by substitution:
\[x + y = 5\] \[x = 5 - y\]This will be substituted into the second equation for x:
\[x - 2y = 2\] \[(5 - y) - 2y = 2\]Now, solve for y:
\[5 - 3y = 2\] \[-3y = 2 - 5\] \[-3y = -3\] \[y = 1\]Now, substitute this value back into the first equation and solve for x:
\[x = 5 - 1\] \[x = 4\]The solution of the system is \(x = 4\), \(y = 1\). These values work in both equations.
Elimination
In elimination, the equations are added or subtracted to eliminate one of the variables. An equation can be multiplied as well. The goal is to get coefficients of the same variable to be the same or opposite in both equations.
For the same system, multiply the first equation by 2 to get:
\[2x + 2y = 10\]The other equation is \(x - 2y = 2\).
Notice that the coefficient of y is opposite. If the equations are added, y will be eliminated:
\[2x + 2y = 10\] \[x - 2y = 2\] \[3x = 12\] \[x = 4\]Substitute this back into either equation to get \(y = 1\).
All Study Guides for the TSIA2 are now available as downloadable PDFs