Mathematics: Geometric and Spatial Reasoning Study Guide for the TSIA2

Comparing Geometric Figures

Geometric figures can be compared to each other using the descriptive terms discussed below.

Symmetry

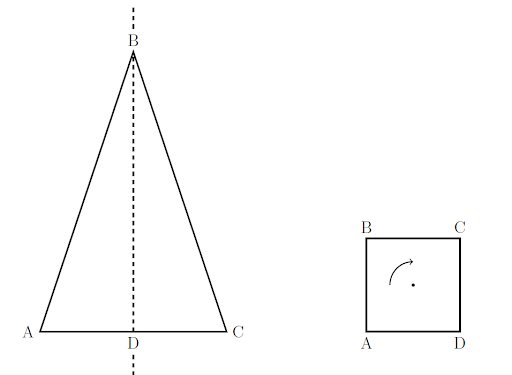
A figure is symmetrical when it can undergo a transformation and appear unchanged. If it is split in half by a line and rotated around that line unchanged, it has line symmetry. If it is rotated around a point by less than 360 degrees and is unchanged, it has rotational symmetry.

In the figure below, \(\Delta \text{ABC}\) is symmetric with respect to the dotted line \(\overleftrightarrow{\text{BD}}\).
\(\overleftrightarrow{\text{BD}}\) is the line of symmetry.

If \(\square{\text{ABCD}}\) is rotated \(90^\circ\) clockwise around its center point, the new image will coincide with the original figure.

Congruence

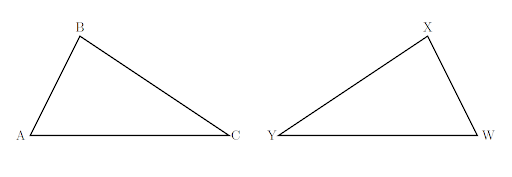
Two figures are congruent if all the angles are equal and all the sides are equal. A series of transformations could superimpose one of them fitting exactly on top of the other.

In this figure, \(\Delta\text{ABC}\) is congruent to \(\Delta\text{WXY}\).

Similarity

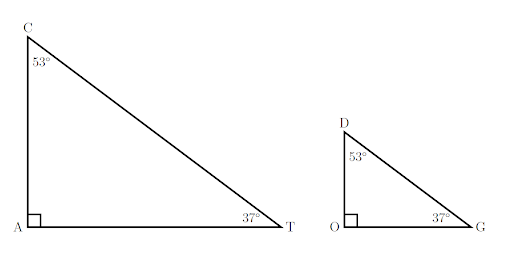
Two figures are similar if the angles are the same but the lengths of the side differ by the same proportion. One of them could be dilated and superimposed on the other. In other words, a dilation produces a pair of similar figures.

Here, \(\Delta\text{CAT}\) is similar to \(\Delta\text{DOG}\).

Transformations

Transformations describe ways in which a polygon might change position in the plane. The properties of the polygon do not change. You can perform these to compare two figures and determine the existence of similarity and congruence.

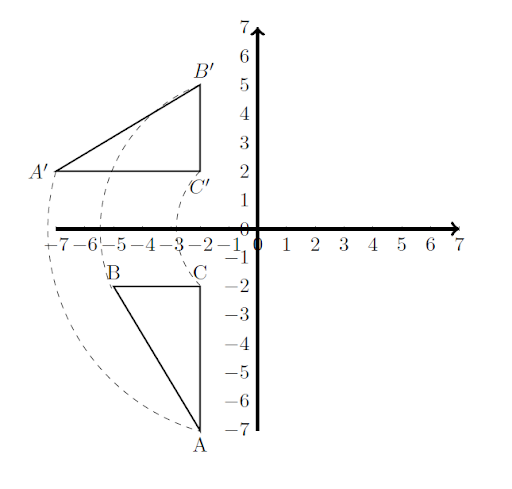
Rotation—In a rotation, the figure is turned around a fixed point.

In this figure, triangle ABC is rotated \(-90^\circ\) about the point \((0,0)\) to the new position A’B’C’.

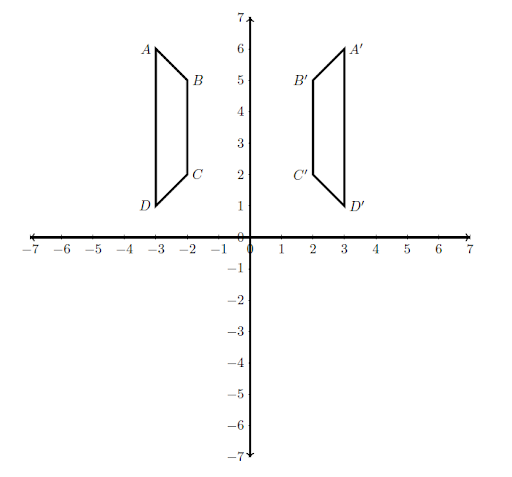
Translation—In a translation, all of the points are moved in the same direction and distance, as if it were slid across the plane. Triangle ABC is translated to A’B’C’.

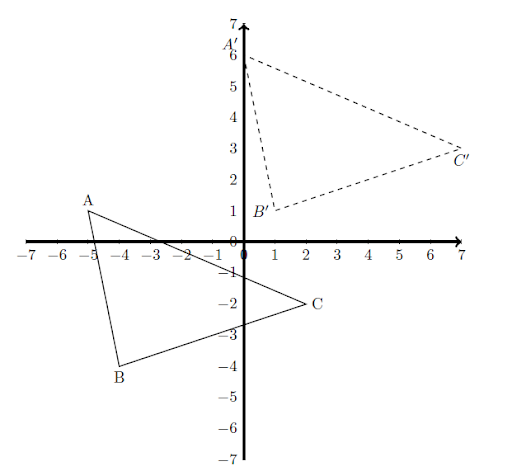
Reflection—A reflection flips the figure across a specified line, called the line of reflection. Quadrilateral ABCD is reflected across the \(x-\)axis to A’B’C’D’.

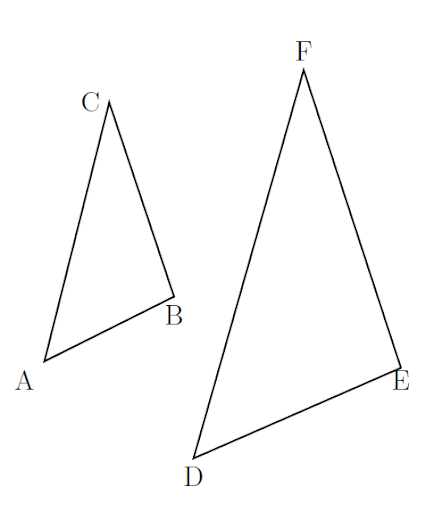
Dilation—A dilation preserves the size of the angles but changes the lengths of the sides by the same proportion. The effect is to shrink or enlarge the figure. Triangle ABC has been dilated to form triangle DEF. The reverse is also true.

Right Triangle Relationships

You will need to be able to apply these principles to solve for missing sides in right triangles.

The Pythagorean Theorem

The Pythagorean theorem is the best known and most widely applied property of right triangles. If the hypotenuse has length \(c\) and the legs have lengths \(a\) and \(b\), then the Pythagorean theorem is given by the formula \(c^{2} = a^{2} + b^{2}\).

Using the Pythagorean Theorem to Solve for Unknown Sides

You will often see problems in which two sides of a right triangle are given and you are asked to find the third side. For example, suppose a leg of a right triangle is \(7\) and the hypotenuse is \(25\). How long is the other leg?

\[a^2+b^2=c^2\] \[7^2+b^2=25^2\] \[49+b^2 = 625\] \[b^2 = 625-49\] \[b^2 = 576\] \[b=24\]

Using the Pythagorean Theorem to Solve a Building Problem

A builder has put stakes in the ground to mark a rectangular area where she wants to pour concrete.To make sure the rectangle has true right angles, she measures the two sides and the diagonal of the rectangle. If the two sides measure \(27\) ft and \(36\) ft, how long should the diagonal be to make sure the corners are right angles?

If the corners are true right angles, then the diagonal of the rectangle will make two right triangles and you can use the pythagorean theorem to check the diagonal. The calculation below shows that the diagonal needs to be \(45\) ft.

\[a^2+b^2=c^2\] \[27^2+36^2=c^2\] \[729+1296 = c^2\] \[2025 = c^2\] \[45 = c\]

Special Right Triangles

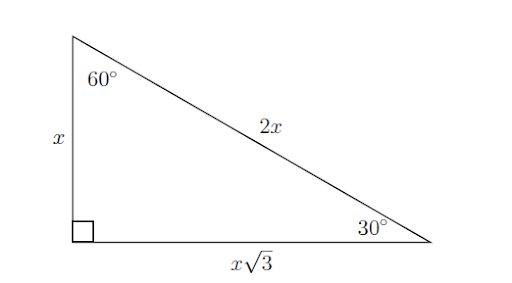
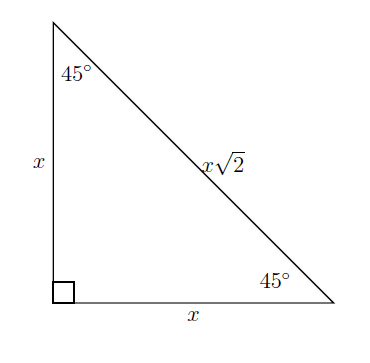
Two different triangles pop up often in geometry and trigonometry: the \(45^\circ-45^\circ-90^\circ\) triangle and the \(30^\circ-60^\circ-90^\circ\) triangle. It’s worth memorizing the values of the sides.

Notice that in the \(30^\circ-60^\circ-90^\circ\) triangle, the shorter leg is opposite the \(30^\circ\) angle. (In any triangle the shortest side is always opposite the smallest angle and the longest side is always opposite the largest angle.) We will use these triangles in the trigonometry section.