Mathematics: Levels E, M, D, and A Study Guide for the TABE Test
Page 1
General Information
The TABE test levels are L, E, M, D, and A and the tests become more difficult in this order. You will see letter designations in this study guide: L, E, M, D, and/or A. These indicate the level of TABE Mathematics test at which you will be assessed on that skill. Note that all skills from lower test levels may be assessed at the higher test levels. So, you should make sure you are fluent in every skill listed for your level as well as those on previous levels. For example, if you are studying for test level M, be sure you understand and can use all skills from level E, as well.
The TABE Testing Procedure
First, you will be given a locator test in mathematics that will determine the level of your first TABE Mathematics test. This short test is given in two 10-minute parts.
No matter which TABE level you take after the locator test, you will have 65 minutes to complete the entire level E, M, D, or A test. The level E test has only one part, timed for 65 minutes. Levels M, D, and A are given in two parts and the time limits for these parts vary with the test level but combine to equal 65 minutes.
Using Our TABE Mathematics Study Guide
The level L Mathematics test is read out loud to students. We do not provide preparation for that level here, but you can see what skills are covered in level L in the percentage of coverage charts for each concept area.
In this study guide, concepts are discussed covering the whole range of difficulty between levels E and A, and the skills areas are mostly arranged in order of difficulty and the order they would have been taught in school. Work through the easiest parts first and continue to the more complex ones as you gain skills. Be sure to look at the percentage of coverage noted for the test you are preparing for and remember that once a skill is tested, you will be responsible for it at higher levels, regardless of whether it is actually tested at those levels.
TABE Mathematics Test Time Limits
Here are the time divisions for each test level:
| Level | Test Section 1 | Test Section 2 |
|---|---|---|
| M | 55 minutes | 10 minutes |
| D | 35 minutes | 30 minutes |
| A | 30 minutes | 35 minutes |
Use of a Calculator
If you are taking the TABE Mathematics Tests on levels M, D, or A, you may use a calculator for Section 2 of the test. For level M, you may use a four-function calculator. Levels D and A permit the use of a scientific calculator and you can view this list of accepted calculators. If you are taking the online version of the TABE, the appropriate calculator will appear on your screen during the math section that allows calculator use.
Formula Sheets
When you take the TABE Locator Test or Levels E, M, D, or A of the TABE Mathematics Test, you will be given a list of formulas to use during the test. The number and types of formulas differ for each test level. Look at this list of TABE math formulas so you’ll know what to expect. (There is one page for each test level.)
Measurement and Data: Part 1
Percentage of Test Level Specifically Assessing Measurement and Data (— = Assumed)
| L | E | M | D | A |
|---|---|---|---|---|
| 11% | 28% | 15% | — | — |
Measuring is a mathematical method of assigning a number or value to the quantity or size of a particular object based on standards, calculations, formulas, and units. The distance between two points is a measure of length. The size of a flat surface or plane is measured by determining its area. The capacity of or space occupied by a three-dimensional object is measured by calculating its volume. Measurement can be done on almost anything that can be quantified, including time, weight, mass, force, speed, angles, density, temperature, and much more.
The word data can refer to a set of measurements or statistics, for example, a list of heights of each student in a classroom or the amount of rain that fell each day of the month. Although in written work you will often see data as a plural (“The data are clear.”), it’s also commonly used as a singular word (“Our data is incomplete.”).
Measuring Length
Though it’s probably obvious, length is just another word for distance, usually used to mean the longest dimension of an object. The units used are chosen depending on the size of the thing to be measured; larger units like miles or kilometers for big things, and smaller units, like inches or centimeters, for small things.
Measuring with Objects
Although we have standard units for measuring length, there’s nothing to stop us from picking any object to be our own personal length unit. For example, we could use a dollar bill as a unit to measure the length of a table. Start at one end and start laying down bills, each one touching the end of the one before it. When you get to the other end of the table, count the bills you laid down. Maybe it’s 11. Then you could say that the table length is 11 bills. This is basically the way any distance is measured, by putting units down one after the other.
Suppose, instead of a dollar bill, you chose a playing card for a unit to measure the table. What would be different about your length number now? It would be bigger, right? It’s a basic idea: the smaller the unit, the more of them it will take.
Measuring with Tools
A biology student collected eight maple leaves and measured their widths as shown in the table below.
| Width (inches) | Number of Leaves |
|---|---|
| \(4\frac{1}{2}\) | \(2\) |
| \(4\frac{3}{4}\) | \(1\) |
| \(5\) | \(3\) |
| \(5\frac{1}{2}\) | \(2\) |
This data can also be shown as a line plot. Each X represents one leaf’s width, eight Xs for eight leaves. You can see, for example, that three Xs are in the 5 column, showing that three leaves had a width of five inches.

Estimating Length
To estimate lengths, it’s a good idea to remember measurements of a few common things.
-
A U.S. quarter is about an inch across.
-
A U.S. man’s size twelve shoe is about a foot (twelve inches) long.
-
A yard is three feet.
-
A meter is close enough to a yard for estimating.
-
A foot is about thirty centimeters.
Comparing Measurements
If Angie’s puppy is 22 centimeters long and Jim’s cat is 34 centimeters long, what would you do to find out how much longer the cat is than the puppy? Simple, right? Subtract the two and get 12 centimeters.
Converting Measurements
The common measurement units encountered in TABE math are:
-
feet (ft), inches (in), centimeters (cm), meters (m), kilometers (km) – for distances and lengths
-
square meters (sq m), square inches (sq in), square feet (sq ft) – for areas
-
cubic feet (cu ft), cubic meters (cu m), liters (L), pints (pt), gallons (gal) – for volume and capacity
It is important to be familiar with the process of converting one unit to another. There are two main systems of measurement: the metric system (meter, grams, liters) and the U.S. standard units (feet, pounds, gallons).
A unit can be converted to another unit within its system (from feet to inches), or to another unit in the other system (from meters to inches). The important thing to remember when solving measurement problems or math questions involving measurement units is to convert the different units into a common unit.
For instance, if you need to get the total length of poles with lengths of 3 m, 6 ft, 40 in, and 5’10”, make sure to convert the lengths to one unit first before proceeding to addition. If the answer choices are given in feet, common sense dictates that you should convert all values to feet. Note: You may find instances in which inches is represented by quotes (“) and feet is expressed by an apostrophe (‘).
Here’s a very useful and reliable way to convert measurements. To convert 45 m/s (meters per second) to mph (miles per hour), write the value to be converted as a fraction:
\[\frac {45\;m}{s}\]Multiply by the conversion factors, also written as fractions:
\[\frac {45\;m}{s} \cdot \frac {1\;mi}{1\text{,}609\;m} \cdot \frac{3\text{,}600\;s}{1\;hr} =\]Tip: Take note that conversion factors are written in such a way that the same units can be canceled later (e.g., \(m\) in the numerator will later cancel out with the \(m\) in the denominator of the conversion factor).
Cancel out the same units occurring in the numerator and denominator. Multiply all numerators, and multiply all denominators. Divide the resulting numerator by the resulting denominator. Affix the units that have not been canceled.
\[\require{cancel} \frac {45\;\cancel{m}}{\cancel{s}} \cdot \frac {1\;mi}{1\text{,}609\;\cancel{m}} \cdot \frac{3\text{,}600\;\cancel{s}}{1\;hr} = 100.68\; mi/h = 100.68\; mph\]It’s important, of course, to be familiar with basic conversion factors. The following is a list of some basic conversions. It is in no way exhaustive, but it will give you an idea of what to explore from other resources.
1 foot = 12 inches
1 yard = 3 feet
1 inch = 2.54 centimeters
1 mile = 5,280 feet
1 ton = 2,000 pounds
1 kilogram = 2.2 pounds
1 liter = 1,000 milliliters
1 milliliter = 1 cubic centimeter
1 hour = 60 minutes
1 hour = 3,600 seconds
Solving Measurement Problems
Given the line plot below, use operations on fractions to calculate the average weight of the watermelons.
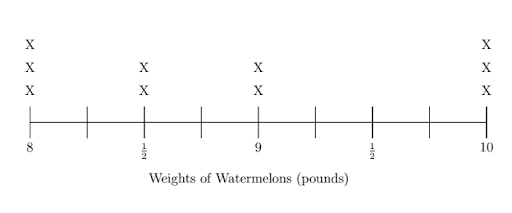
First, account for each watermelon’s weight.
\(3 \times 8 = 24\) pounds
\(2 \times 8\frac{1}{2} = 17\) pounds
\(2 \times 9 = 18\) pounds
\(3 \times 10 = 30\) pounds
\(\underline{ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\)
Total: \(10\) watermelons weigh \(89\) pounds
To get the average weight, we divide the total weight by the number of watermelons:
\(\frac{89}{10} = \frac{80}{10} + \frac{9}{10} = 8\frac{9}{10}\) pounds.
Representing and Interpreting Data
Once data has been collected, it can be organized and represented in different ways. A good first step is to put it in a table, like the one below.
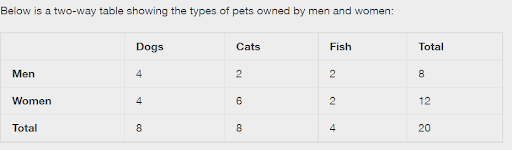
Retrieved from: https://openstax.org/books/introductory-business-statistics example 2.7.
For a simple data set like this one, the table itself is quite easy to interpret. More complicated sets need other ways to show the data, the most common way being some kind of graph.
Categories of Data
You should be able to interpret a data table like the one below. Following the table are typical questions you may be asked:
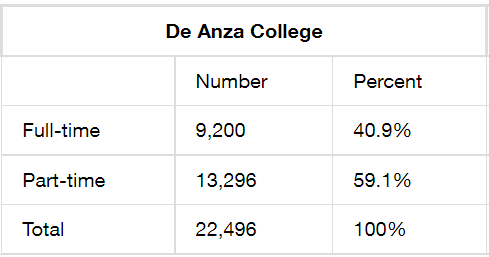
Retrieved from: https://openstax.org/books/introductory-business-statistics Table 1.2.
Are there more full-time or part-time students?
Answer: Part-time
How many more part-time students than full-time are there?
Answer: 4,096
Is the ratio of full-time to part-time students greater than or less than one?
Answer: Less than one, because it is \(\frac{9\text{,}200}{13\text{,}296}\)
Types of Graphs
There are several types of graphs: pie, bar, line, dot, pictograph, scatter plot, and histogram. Graphs contain information displayed visually, including the answer to your test question. All you need to do is understand these graphs and know how to make use of the data contained in them.
As in charts, read the title first. It summarizes what the graph represents. Read the vertical and horizontal labels and the legend. These graphs compare values of one thing/category versus other things/categories over another dimension (a period of time, for instance). A line graph may compare the population of students in classrooms A, B, and C, for the past three years. The vertical label may indicate the numbers, while the horizontal label may indicate the years. The legend may indicate the different colors designated for the classrooms.
Here is an example of a bar graph with seven categories, showing the ethnicity of students in a school.
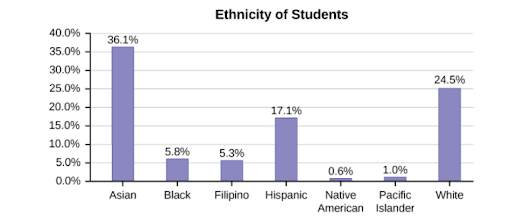
Retrieved from: https://openstax.org/books/introductory-business-statistics Figure 1.7.
A pie graph is quite unique because it does not have the vertical and horizontal labels that the other graphs have. Instead, it compares values relative to other values using percent, fraction, or ratio.
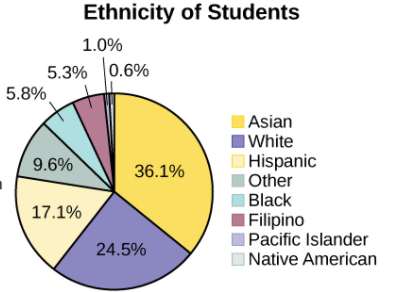
Retrieved from: https://openstax.org/books/introductory-business-statistics Figure 1.10
Data can be represented in a more interesting way using a picture graph (also referred to as a pictograph). This type of graph uses pictures to represent quantities. Picture graphs can be of two types. The simplest picture graph uses one picture for every item in the data set. Here is an example of a simple picture graph:
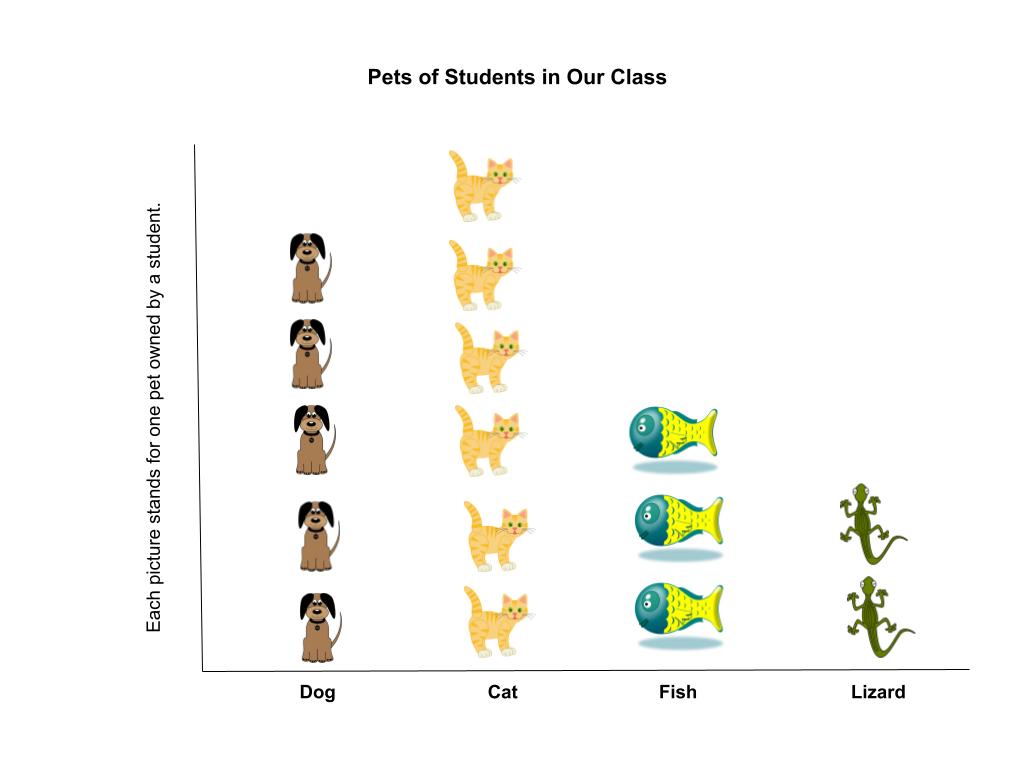
According to the graph, this classroom of children did not accumulate too many pets. The number each type of pet owned by children in this class is:
Dogs: 5
Cats: 6
Fish: 3
Lizards: 2
When larger numbers are involved, you can also use one picture to represent more than one item in the data set. We call this a scaled picture graph. Below, the same number of the same pictures is used, but notice the title and the explanation next to the left side. This graph may look a lot like the graph above, but it does not communicate the same information at all.
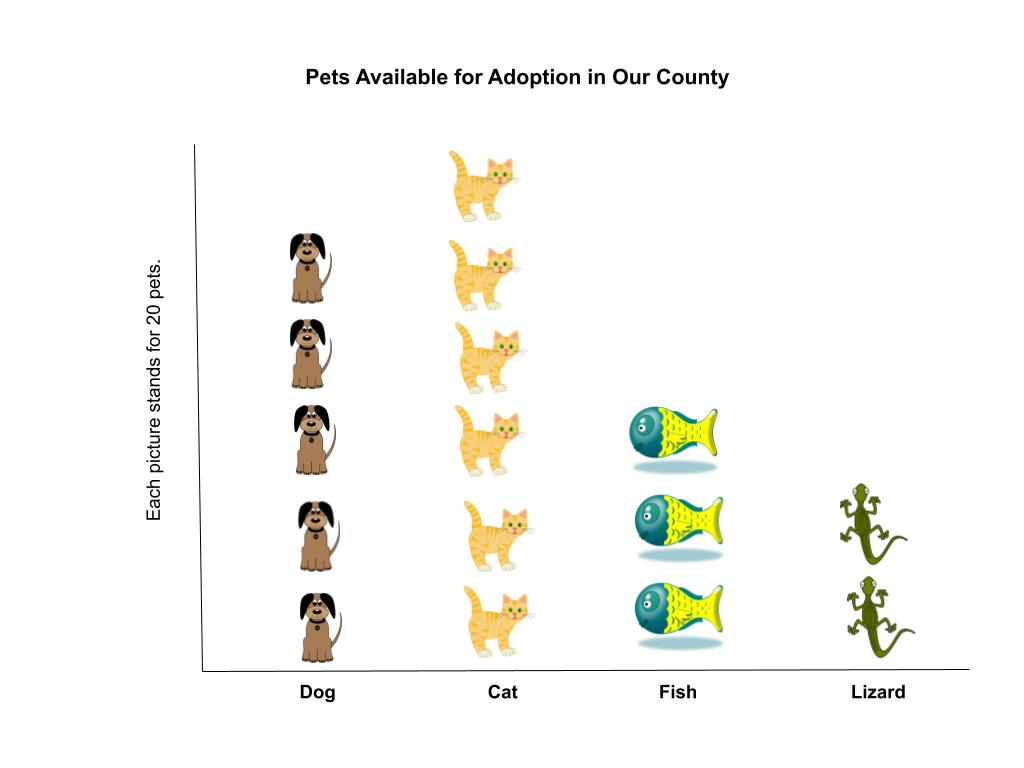
Obviously, there will be many more animals across a county than there are in students’ homes. The totals represented in each category of this graph are:
Dogs: 100
Cats: 120
Fish: 60
Lizards: 40
You can see how important it is to read every part of a graph, including all captions and other information. If you don’t, you may not come away with accurate information.
Solving Data Problems
The numbers of students at Albert Einstein High School who bought their lunch in a certain week are shown in the bar graph below. Notice that the actual number of students is 100 times larger than the scale number shown on the vertical axis. That is, 2 means 200, and so on. We call this type of graph a scaled graph as well. It has small numbers representing much larger numbers. It is very useful when the data comes in larger sets. This one is a scaled bar graph.
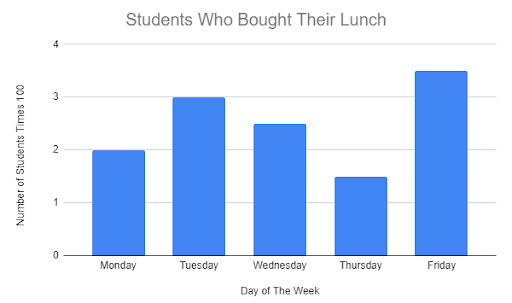
Approximately how many more lunches were bought on Tuesday than on Thursday?
On Tuesday, approximately 300 lunches were bought, and on Thursday approximately 150 lunches were bought.
The difference between the two is 300 - 150 = 150.
All Study Guides for the TABE Test are now available as downloadable PDFs