Mathematics: Levels E, M, D, and A Study Guide for the TABE Test
Page 2
Measurement and Data: Part 2
Percentage of Test Level Specifically Assessing Measurement and Data (— = Assumed)
| L | E | M | D | A |
|---|---|---|---|---|
| 11% | 28% | 15% | — | — |
Measuring Time
Common time units are shown in the list below.
60 seconds = 1 minute
60 minutes = 1 hour
24 hours = 1 day
7 days = 1 week
365 days ≆ 52 weeks = 1 year
Note: Even though one year is considered to equal 52 weeks, there is actually one extra day. This is how we end up with 365 days.
Basic Time Measurement
Be able to tell time and write it in colon notation (e.g., 6:19, 12:00). Time can be thought of in two different ways; as a time of day, or as the length of time that has passed (called a time interval).
Times are written with hours first followed by a colon, then the number of minutes. If the time on a clock is 20 minutes past 10, for example, it would be written as 10:20. This answers the question, “What time is it?”
Another use of this colon notation is in writing how much time has gone by. If you drove straight through from Boston to San Diego, it might take you something like 26 hours and 30 minutes, which would be written as 26:30. This answers the question, “How long did it take?”
Solving Problems Using Time Measurements
Be able to solve problems about time intervals, like the ones below.
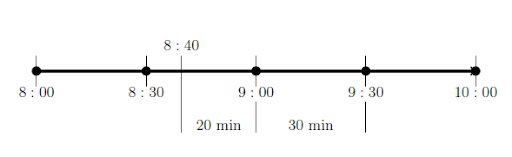
A flight from Detroit leaves at 8:40 a.m. and arrives in Chicago at 9:30 a.m. How long did the flight take? The easiest way to show this is to picture the times on a number line. The figure shows that there are 20 minutes from 8:40 to 9:00 and 30 minutes from 9:00 to 9:30. That adds up to 50 minutes.
Measuring Perimeter
The perimeter is the distance around the boundary of a figure. If you know the lengths of the sides, you just add them up to get the perimeter. Sometimes a perimeter problem has a little twist. You are given the perimeter and all but one of the sides and asked for the length of the missing side.
For example, a six-sided polygon has a perimeter of \(38\) and five of its sides have lengths of \(3, \,7,\, 7,\, 6,\) and \(9\). How long is the sixth side?
If we add the five sides we know, and the missing side, we will get \(38\), so we can write this:
\[3+7+7+6+9+\_\_\_\_=38\] \[32 + \_\_\_\_= 38\]The missing side must be \(6\).
Here’s a different kind of problem.
If you had \(16\) feet of fencing to make a small rectangular turtle pen, would any length and width you used give the same area inside?
Try a \(4 \times 4\) pen and a \(2 \times 6\) pen. They both have the same perimeter.
\[4+4+4+4=16\ \ \ \ \ \ \ 2+2+6+6 = 16\]The \(4 \times 4\) has an area of \(4 \times 4 = 16\). The \(2 \times 6\) pen has an area of \(2 \times 6 = 12\).
So the answer is no, they do not have the same area inside. Length and width make a difference. In fact, a \(4 \times 4\) square gives you the most area possible for \(16\) feet of fencing.
Measuring Mass
Mass is closely related to weight, but not exactly the same. Here’s a comparison:
Weight measures the force of gravity pulling down.
Weight changes from place to place. Take a scale to the Moon and you will see that you weigh less on the Moon than on Earth.
Mass measures how hard it is to start an object moving or to stop an object that’s moving.
Mass doesn’t change from place to place.
Consider kicking a bowling ball with your bare feet. Broken toe and ER trip, right? Is that because of weight or mass? Before you answer, imagine that you could travel to some asteroid in space where standing on a scale would show almost zero weight. Could your toe survive a barefoot kick to a bowling ball there? Could you throw a bowling ball like you would a baseball?
The answer to both questions is “no”, because of mass. The bowling ball will still fight you if you try to speed it up (or slow it down), even though it’s essentially weightless. That’s mass for you.
Using Standard Units to Measure Mass
The standard metric units of mass are the gram (g) and the kilogram (kg). For estimating, think of a kilogram as a bit more than \(2\) pounds (lbs). A liter (L) of water is a bit more than a quart and has a mass of \(1\) kg. A paper clip has a mass of about \(1\) g, and an average banana has a mass of about \(125\) g. Approximations like these can help you to estimate the masses of common objects. To measure masses, it’s common to use a balance or a scale that has been calibrated to read correctly on Earth.
Solving Problems Using Mass
You should be able to solve one-step problems involving masses given in the same units using basic math functions, such as addition, subtraction, multiplication, and division. Sometimes, drawing a picture of the information you have helps you determine what to do.
For example:
Betty Baker wants to bake two dozen cookies. She knows that it takes 2 oz of cookie dough to make 3 cookies. How many ounces of cookie dough will she need? The drawing below is one way to help visualize this procedure by drawing.
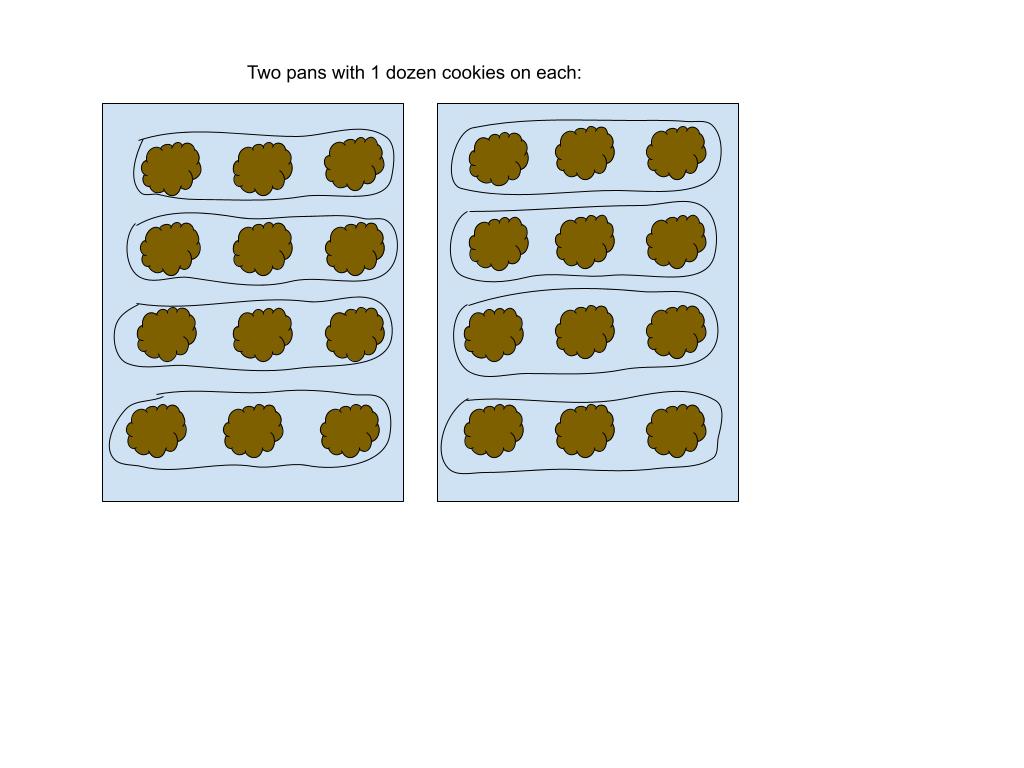
Once you know that she needs to make eight groups of three cookies, you can multiply 8 by 2 oz. She will need 16 ounces of cookie dough.
Measuring Area
Area is the measure of a surface that has been enclosed by a boundary. A common sheet of paper, for example, is a rectangle enclosed by the paper’s edges. A U.S. quarter is a circle enclosed by its round edge. Fairly simple shapes, like rectangles, triangles, circles, and parallelograms, have formulas that can be used to calculate their areas. Oddly shaped things, like golf greens, don’t have simple ways to find their areas.
Some Simple Formulas
Common Area Formulas
| Figure | Formula | Variables |
|---|---|---|
| Rectangle | \(A=l\cdot w\) | l = length w = width |
| Square | \(A = s^2\) | s = side length |
| Triangle | \(A=\frac{1}{2}b\cdot h\) | b = base length h = height |
| Circle | \(A = \pi r^2\) | \(\pi\) = 3.14 r = radius |
Operations and Area
If you totally understand the basic idea of area, you can skip this section.
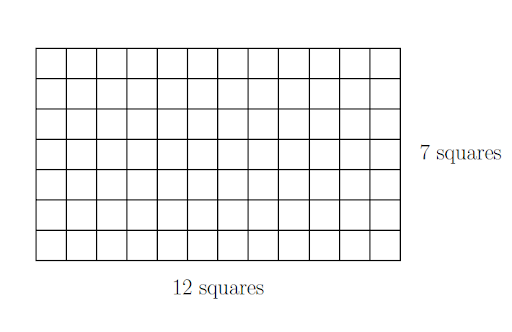
To help understand how area works, we will use the rectangle below to illustrate. Area is measured by finding the number of squares that fit in the figure. How many squares are shown fitting into the rectangle below? We could just count them, but there are quite a few there. We can reason our way to the answer by noticing that there are \(12\) squares in each row. Also, there are \(7\) rows. Rather than add all the squares, we can use multiplication to get the answer.
\(7\) rows of \(12\) squares gives \(7\times12 = 84\). That’s the formula \(A = lw\).
Measuring Volume
Earlier in this guide, we defined area to be the measure of a surface enclosed by a boundary. We can define volume as the measure of space enclosed by a surface, as in a balloon, or multiple surfaces, as in a cube. Earlier, we described the area as the number of squares that would fit into a surface. Volume can be thought of as the number of cubes that can fit into a three-dimensional space. Volume units often have the word “cubic” in them, as with cubic inches, cubic centimeters, cubic feet, and so on. There are also volume units that don’t use the word cubic. For example, we have gallons, liters, milliliters, quarts, and more.
Measuring Liquid Volume
Liquid volumes are often measured with a container that has a scale printed on it, such as a measuring cup in the kitchen or a beaker or graduated cylinder in the science lab. When you are working with liquid measurements, it is sometimes helpful to quickly sketch the amounts in the measuring cup or beaker. This is useful when performing operations with the given amount of liquid.
Retrieved from: https://publicdomainvectors.org/en/free-clipart/Beaker-with-water/52141.html
You should be able to do problems that combine different volumes or divide them in some way. Here are a couple of problems.
If a student has a beaker holding \(520\) mL of water and pours as much as possible into a \(150\) mL beaker, and then pours the rest into a \(500\) mL beaker, how much water will be in the \(500\) mL beaker?
Answer: If you take \(150\) away from \(520\), you will have \(520 - 150 = 370\) mL left. That’s how much goes into the \(500\) mL beaker.
Suppose the student again starts with \(520\) mL of water and uses it to fill \(26\) test tubes, how many mL did each test tube hold?
Answer: Since we are dividing \(520\) in \(26\) ways, that’s a pretty good clue that we need to use division in the problem: \(520\div 26 = 20\) mL in each test tube.
Solid Volume
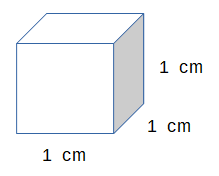
A cube that has dimensions \(1 \times 1 \times 1\) is called a unit cube. The one below happens to be a centimeter unit cube. It represents the volume of a cubic centimeter. There can be unit cubes of any length unit you can think of: a cubic inch, a cubic foot, a cubic yard, a cubic meter, etc. If you are measuring the volume of something really big, like the ocean, you might even want to use cubic miles. Literally any length can be used to make a unit cube. You could imagine a unit cube made of pencil lengths and call it a cubic pencil. It would be kind of a silly thing, really, since no one else would be using cubic pencils for a unit, and you might draw a few odd looks from your fellow students.
One cubic centimeter:
To help visualize cubic units, sketching is a useful tool. The proportions don’t have to be exact for it to represent the number of units you need.
Retrieved from: https://publicdomainvectors.org/en/free-clipart/Dice-building/46859.html
When you’re thinking about measuring the volume of an object, you’re looking to see how many unit cubes will fit into the object. For example, if you stacked 10 one-centimeter unit cubes on top of each other, you will have made a little tower that has a volume of 10 cubic centimeters. Like any other form of measuring, you have a standard unit and you’re trying to see how many of that unit will fit into the object you’re measuring.
Using Operations
Volumes of solids can be calculated using different formulas.
| Figure | Formula | Variables |
|---|---|---|
| Rectangular Solid |
\(V=l w h\) | l = length w = width h = height |
| Cube | \(V = s^3\) | s = edge length |
| Cylinder | \(V=\pi r^2 h\) | r = radius h = height |
| Sphere | \(V = \frac{4}{3}\pi r^3\) | \(\pi\) = 3.14 r = radius |
Using a Number Line
In the next section, you will see some number lines. They are nothing but a line with evenly spaced marks that we label with numbers that get bigger as they go to the right. Number lines are good for giving us a picture of what we are doing when we use addition and subtraction.
Representing Numbers
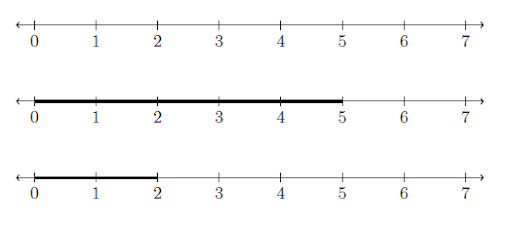
To represent a whole number on a number line, we draw a line from zero to that whole number on the line. For example, The second figure represents the number 5 and the third figure represents the number 2.
Representing Operations
We can show addition by drawing an arrow for each number as shown below. We write these above the line to help make the arrows clear. When adding, the arrows point to the right. This shows 2 + 4 = 6.
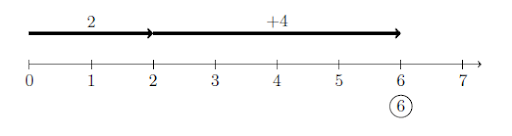
To show subtraction, like 4 - 2 = 2, we show the larger number going to the right, and the subtracted number going left from the first number.
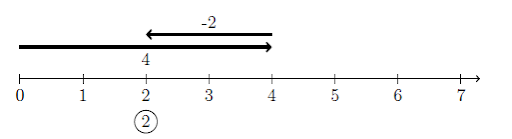
Measuring Angles
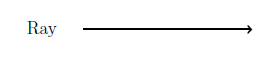
In geometry, a line that has a beginning but no end is known as a ray. We imagine that it goes on forever in the direction of the arrow.
If two rays are joined at their ends, they form an angle. In this figure, the rays share point \(A\), which is called the vertex of the angle. The angle can be named as angle \(A\) or angle \(FAN\), and the word angle is usually replaced by the angle symbol \(\angle\), like so: \(\angle A\) or \(\angle FAN\). The vertex letter is always written in the middle.
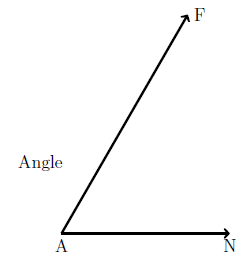
Using a Protractor
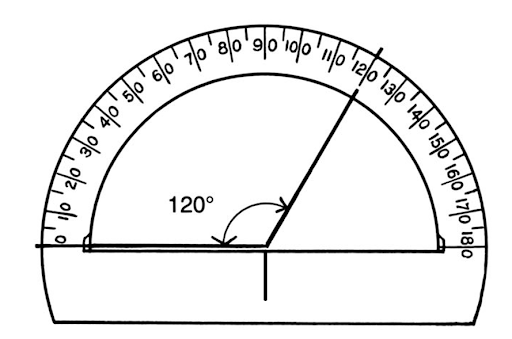
The figure below shows a protractor lined up with a \(120^\circ\) angle. See how the vertex of the angle lines up with the center mark, and one side of the angle lines up with the zero mark. The number of degrees of the angle then lines up with the second side of the angle.
Adding Angles
Two angles can be combined to form a third larger angle as shown below if they have the same vertex (\(A\), in this case) and share a common side (\(\overrightarrow{AN}\)) between them. Their measures can be added together to get the measure of the larger angle they make.
\[\angle NAB + \angle MAN = \angle MAB\] \[25^\circ + 65^\circ = 90^\circ\]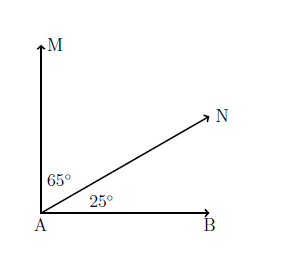
Problem-Solving with Angles
Angles can be subtracted as well as added. Here’s a sample problem.
If \(\angle MOB = 120^\circ\), what is \(\angle MOJ\)?
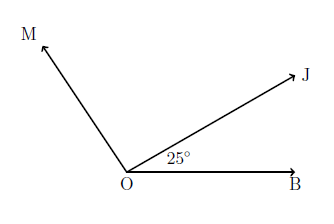
We can see that a \(25^\circ\) angle and \(\angle MOJ\) add up to \(120^\circ\). If we let \(\angle MOJ = x\), we can write this equation:
\[25^\circ + x = 120^\circ\]To get \(x\), we subtract \(25^\circ\) from both sides of the equation:
\[25^\circ + x -25^\circ= 120^\circ - 25^\circ\] \[x = 120^\circ - 25^\circ\] \[x = 95^\circ = \angle MOJ\]Another example:
A huge slice of pie makes an angle of \(145^\circ\). If Jim takes a piece measuring \(50^\circ\), and Maria takes a small sliver measuring \(25^\circ\), what amount (in degrees) of pie is left?
First, we add \(50^\circ + 25^\circ = 75^\circ\).
Then, subtract that from the original piece: \(145^\circ - 75^\circ = 70^\circ\).
All Study Guides for the TABE Test are now available as downloadable PDFs