11th Grade Mathematics: Geometry Study Guide for the SBAC

How to Prepare for the Geometry Questions on the SBAC Mathematics Test

General Information

As in the other math areas tested on the SBAC, the emphasis is on being able to explain the geometry operations and procedures you do and why they work to produce a correct answer. So, be sure you really understand all of them. Also know that geometric ideas may be combined with other math skills to solve problems and that many of them use on this test require a thorough understanding of much simpler geometric concepts.

Skills to Understand and Be Able to Use

Transformations

Transformations are operations that move or change an object from its original state. There are several types of transformations; some preserve the object’s shape and size (referred to as a rigid transformation) and some change the size or shape (referred to as a non-rigid transformation) of an object. You will need to know how to perform both in the coordinate plane.

Definitions

It will be important for you to be comfortable using the terms defined below when performing transformations in the plane with various geometric objects..

angle— An angle is the formation of two rays that share a common endpoint. We often think of an angle being created by taking an initial ray and rotating it about its endpoint to the terminal ray.

circle— The set of all points that are equidistant from a fixed point in a plane.

perpendicular line— A line that intersects another line at a 90 degree angle. Perpendicular lines’ slopes are negative reciprocals of each other. Other terms used are normal and orthogonal.

parallel line— A line is that does not intersect another line in the same plane. Parallel lines have the same slope.

line segment— A portion of a line that can be measured. The measurement is taken between its endpoints.

point— A point describes an exact position in the plane. In the coordinate system a point is defined by an ordered pair \((x, y)\).

line— Geometrically, a line is straight and extends in opposite directions without bound. A line contains line segments and rays.

distance along a line—The length of a line is infinite. The distance along a line that can be measured is the length of the line segment the line contains.

distance around a circular arc— The length of the portion of a circle that is formed by the circle’s central angle. It is also defined as a portion of the circumference of a circle.

Represent Transformations

You will need to determine what type of transformation is produced from one object or function to the next, and if the transformation preserves the shape and size of the object or a function.

Rigid transformations include translations, rotations, and reflections. These types of transformations only move and object but do not change its shape or size. They are also referred to as isometric transformations for this reason. For example, you can reflect \(f(x) = x^2\) about the \(y\)-axis or \(x = 0\) using \(f(-x) = (-x)^2 = x^2\). Notice, the graph of \(f(x)\) is already symmetric around the \(y\)-axis, so it is its own reflection. You should also be able to translate a figure by moving each point in the figure the same distance in the same direction. This type of transformation is also referred to as a glide.

Non-rigid transformations include dilations and compressions which change the size but not the shape and change the size and shape of an object respectively. We will look at dilations shortly.

Describe Rotations and Reflections

You will also need to know how to perform several transformations on an object. If performing one or more transformations on an object returns the object to its original position so it preserves its shape and size, we say the object has symmetry with respect to that transformation(s). Rotating a rectangle about its center point \(90\) degrees in the same direction two times or reflecting a square about either of its diagonals one time are transformations that preserve the shape and position of the object.

A regular polygon has a reflective symmetry. An \(n\)-sided regular polygon has \(\dfrac{n}{2}\) diagonals. You can reflect an \(n\)-sided polygon about each of its diagonals one time and the polygon reflects onto itself.

You will need to transform a figure about a fixed point by rotating the points on the figure by a given angle whose vertex is the fixed point. The points move along the circular arc formed by the angle of rotation. A reflection moves the points on the figure across a line whose distance is equal to the distance the original point is to the line of reflection. The line segment formed by the point and the reflected point should be perpendicular to the reflected line.

Create Definitions

In addition to representing and describing certain transformations, you’ll be asked to define a transformation given a set of rules. In other words, a transformation will be described using pictures or a mapping rule. You’ll then have to identify which transformation(s) define that rule.

Example: Define the transformation which maps all points \((x,y)\) to \((x-5, y+3)\).

Solution: The property defines a translation. Specifically, it is a translation 5 units left and 3 units up.

Draw Transformations

You will need to be able to perform one or more of the transformations that map one geometric figure onto another. There may be different combinations available to do this. For example, reflecting a square about the origin in the coordinate system is equivalent to reflecting the square about the \(x\)-axis then the \(y\)-axis.

You will also need to determine if a geometric figure has symmetry and be able to show the number of transformations and combinations of transformations that map the figure onto itself.

Congruence

Congruence means that two or more geometric figures have the same size and shape. So, the corresponding sides and angles for two or more geometric figures have the same length and measure respectively. This implies that any motion transforming a geometric figure to produce a congruent geometric figure must be a rigid motion.

Describing Rigid Motions

You will need to know the different types of rigid motion that can be used to transform one geometric figure to another congruent geometric figure. These rigid motions include translations, reflections, and rotations. There may be one or many of these types of transformations used when showing one geometric figure is congruent to another.

Using the Definition of Congruence

You will need to show that two triangles are congruent through one or more rigid motions since the size and shape of both triangles remain the same. For example, if points \(A\), \(B\), and \(C\) are translated \(3\) units to the right to form points \(X\), \(Y\), and \(Z\) respectively, then \(\triangle{ABC} \cong \triangle{XYZ}\) since the translation does not change the lengths of the corresponding sides or the measure of the corresponding angles when mapping \(\triangle{ABC}\) to \(\triangle{XYZ}\). This also means that if the corresponding parts of two triangles are congruent (CPCTC), then the two triangles must also be congruent.

Using Triangle Congruence

There can also be a minimum amount of information given to show that two triangles are congruent.

• If three sides of one triangle are congruent to three sides of another triangle, the two triangles are congruent by the Side-Side-Side(SSS) theorem.
• If two sides and an included angle (the angle formed by the two sides) of one triangle are congruent to another triangle, the two triangles are congruent by the Side-Angle-Side(SAS) theorem.
• And, if two angles and the included side (the side between the two angles) are congruent to another triangle, the two triangles are congruent by the Angle-Side-Angle(ASA) theorem.

In each case, all three of the corresponding angles and sides are congruent for the two triangles by CPCTC.

Dilations

You will need to be able to dilate a geometric figure or a function. As noted earlier, a dilation does not change the shape but only the size of a figure. Some things to remember are:

• A dilation does not change the measure of an angle.
• Parallel lines remain parallel, but a line segment that is dilated changes length.

Center

The center of a dilation is the fixed point in the plane where all other points are extended (lengthened) some distance in the same direction by some constant or contracted (shortened) some distance in the same direction by some constant.

Scale Factor

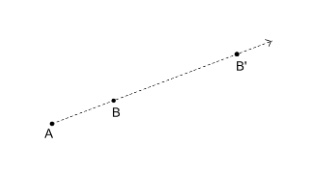
You may need to determine the scale factor used for a given dilation. The scale factor is the constant used that extends or contracts the points of a figure from the center of dilation. In the diagram below, segment \(\overline{AB}\) is extended to produce \(\overline{AB’}\) by multiplying the length of \(\overline{AB}\) by some constant, \(k\) so that \(AB’ = k \cdot AB\). Equivalently, \(k= \dfrac{AB’}{AB}\) where \(A\) is the center of the dilation. Here, since \(AB’ \gt AB\) , then \(k \gt 1\), meaning \(B’\) extends beyond \(B\). If \(k \lt 1\), then \(AB’ \lt AB\) and \(B’\) is contracted or between \(A\) and \(B\).

Similarity

Similarity is like congruence of geometric figures but the figures do not have to be (and typically are not) the same size. Dilation is a key transformation when drawing similar geometric figures.

The Definition of Similarity

You will need to determine if two geometric figures are similar by showing that their corresponding angles are congruent and corresponding sides are proportional. A dilation is a similarity transformation since the sides that are transformed change by the same factor.

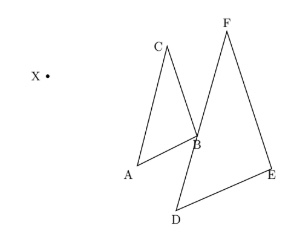
A dilation is also a similarity transformation. If, in the image below, \(\triangle{ABC}\) is dilated by some constant so that \(A, B,\) and \(C\) are transformed to \(D, E,\) and \(F\), thus creating \(\triangle{DEF}\), \(\triangle{ABC} \sim \triangle{DEF}\), where angles \(\angle{A}, \angle{B},\) and \(\angle{C}\) are congruent to angles \(\angle{D}, \angle{E},\) and \(\angle{F}\), respectively. Also, corresponding sides are proportional, \(\dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{AC}{DF}\), by dilation similarity.

Properties of Similarity Transformations

If two corresponding angles of one triangle are congruent to another triangle, the 3rd pair of corresponding angles must also be congruent. The AA (angle-angle) similarity criterion is the same as showing all the corresponding angles are congruent due to the sum of the angle being equal to \(180\) degrees. If the dilation transformation is used to produce the 2nd triangle, you can say the triangles are similar by the AA criterion.