How to Prepare for the Function Questions on the SBAC Mathematics Test

General Information

Functions give us tools to use in solving mathematical problems. They’re like keys that unlock the answers to complex mathematical questions. You’ll need to be fluent in their creation and use and be able to explain the whys and wherefores of their construction and their role in problem-solving.

Skills to Understand and Be Able to Use

Understanding Functions

Equations are used to show a relationship between two quantities. Functions are similar, but use a rather different way of thinking and writing. The sections below elaborate on the concept and notation of functions.

What Is a Function?

The basic idea of a function is that it is a statement that relates one set of values (think of these as the input values) with a second set of values (think of these as output values.) For example, say we think of taking any number we like and cubing it. Input a 2 and get 8 as a result. Input 0.5 and get 0.125 as a result. We can think of x as the input value and \(x^{3}\) as the result.

In function notation, we write \(f(x)=x^3\), where \(f(x)\) means function of x and we read it as f of x. The right side shows what to do to x to produce an output value. The left side represents the output of the operation on x.

We will look at linear and exponential functions, along with arithmetic and geometric sequences.

Parts of a Function

Not all relations are functions. To be a function, each input value has to produce only one output value. It is OK for two different inputs to produce the same output, but not vice versa. To graph a function, it makes sense to use f(x) for the vertical axis instead of y, although you will often see y used when a function is being graphed.

Domain and Range

The set of values that are used as input values is known as the domain of the function, and the set of values that are outputs of the function is known as the range.

Elements

The values in the domain and the range are known as the elements of the domain and range.

Function Notation

As stated earlier, the symbol f(x) is used to denote a function, as in \(f(x)=9x+4\). Sometimes letters other than f are used, commonly g(x) or h(x), but any letter can be used. These are all read in the same way: “f of x”, “g of x”, or “h of x”.

A common problem you will run into will ask you to evaluate a function for a certain input value. For example:

If \(f(x) =9x+4\), what is \(f(2)\)?

This is asking you to substitute 2 for x in the function and see what you get.

\[f(2)=9(2) + 4=22\]

So \(22\) is the value of the function when the input is \(2\), written \(f(2)=22\).

Functions are often used in the context of representing (modeling) certain situations. For example, the function \(V(t)=32t\) is used to represent the velocity of a freely falling object on earth. After falling for 3 seconds, \(V(3)=32 \times 3\), or \(V(3)=96\).

Sequences are Functions

It’s common in working with arithmetic sequences to come across the formula \(a_{n}=a_{1}+d(n-1)\), where \(a_{n}\) represents the \(n^{th}\) term of an arithmetic sequence, \(a_{1}\) represents the first term, d the common difference between consecutive terms, and n the number of the term you seek. This can just as well be thought of as a function of n, written this way: \(f(n)=f(1)+d(n-1)\), which is an explicit definition. If you know the first term and the common difference, you can find any term you want in one calculation.

Sometimes a sequence is defined recursively, meaning the first term is given and each following term is defined in terms of the term before it. For example, {2, 5, 8, 11, …} can be defined this way: \(a_{1}=2\) and \(a_{n}=a_{n-1}+3\). In function notation it could be written \(f(1)=2\) and \(f(n)=f(n-1)+3\). Notice that, to use this recursive definition to find, say, the tenth term, you must first know what the ninth term is, but before that, the eighth term, and so on.

A well known sequence in math is the Fibonacci sequence: \(0,\ 1,\ 1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21, \ …\), in which each term is obtained by adding the previous two terms. The first two terms are defined to be 0 and 1, and then all the rest of the terms can be produced by successively adding two previous terms. As a recursive function definition, it would look like this:

\(f(0) = 0\), \(f(1) = 1\), \(f(n) = f(n-1) + f(n-2)\)

Interpreting Functions

Suppose a foot traffic counter is installed in the doorway of a store and the function \(n(t)\) represents the number of customers, \(n\), that pass through during the \(t^{th}\) hour after opening. What is the physical meaning of the statement \(n(2) > n(7)\)? This is an example of interpreting a function in the context of a specific situation. \(n(2)\) is the number of people passing through during the \(2^{nd}\) hour and it is larger than \(n(7)\),the number passing in the \(7^{th}\) hour. That’s the answer to the question.

You should be able to do this kind of interpretation for a variety of functions, particularly linear, quadratic, and exponential ones.

Relationships

Given a description of a function, you should be able to draw its graph using the same key features as you would in graphing an equation. The graph above is for \(f(x)=x^{3}-4x\). Just as with equations, you can use the three zeros of the function, -2, 0, and 2,along with a relative maximum at about \((-1.1,3)\) and a relative minimum at about \((1.1, -3)\) to graph the function. Other useful features are regions that are positive or negative, or increasing or decreasing. Graphs can be periodic. (We’re looking at you, trigonometry.)

Graphs

Describe an appropriate domain for a given function. For example if a weekly paycheck is represented by the function \(p(h)=14h\), an appropriate domain could be all positive real numbers. In practice, though, the numbers of hours worked may be rounded to the nearest quarter hour. In that case, the domain would be {0, 0.25, 0.50, 0.75, 1, 1.25, …}. (Of course there are only 168 hours in a week, so that would impose an upper limit of 168 on the domain. Chances are, though, that no one will ever work that many hours, though there are some weeks it may feel that way.)

Rate of Change

If some quantity is a linear function of time, for example, distance traveled, the rate of change is simply the slope of the function’s graph. If the graph is non-linear, two points are chosen on the graph or in a table to define an interval, and the slope over that interval will be the average rate of change of the function in that interval.

Comparing and Analyzing Functions

To compare two functions where one may be in graph form, say, and the other may be shown algebraically or in a table, a good approach is to change one representation into a form to match the other. For the example of having a graph and a table to compare, try changing the data table to a graph. That way any differences or similarities will be visually apparent. In a simple linear function, you can probably compare the graph and the algebraic version as is.

Linear and Quadratic Functions

Your experience with graphing linear and quadratic equations should make it easy to apply the same thinking to linear and quadratic functions. Intercepts on the x and y axes and maxima and minima in parabolas are treated the same way, no matter if you’re looking at \(y=x^{2}-25\) or \(f(x)=x^{2}-25\).

Polynomial Functions

If you are given a polynomial to graph, there’s a good chance it will be factorable. For example: \(f(x)=x^{3}-x\) factors as \(f(x)=(x)(x+1)(x-1)\). If you set each factor equal to zero and solve, you will get \(x=0,\ x=-1,\ x=1\). These are the zeros of the function and they tell you where its graph crosses the x-axis.

To see the behavior of the graph at the ends, try putting something larger, like 10, in for x. Does f(10) get larger? Yes indeed: 990. Then the graph is rising to the right. Now try -10 for x. That gives you -990, which means the graph is falling on the left. Some polynomials rise on both sides and some fall on both sides.

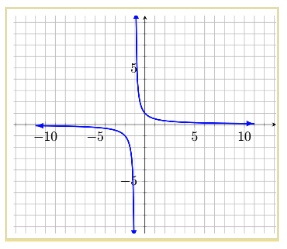
Rational Functions

Rational functions are in fractional form with some form of x in the denominator, by itself or with other terms, and often in the numerator as well. Since the denominator is not allowed to be zero, there will always be some value(s) for x that are not allowed in the domain of the function.

A simple example is \(f(x)=\dfrac{1}{x+1}\), the graph above. The value of x can never be -1, which means that when you graph the function, the graph cannot exist at \(x=-1\). There will be an asymptote at \(x=-1\). The graph will approach \(x=-1\) from both sides, but never quite get there. You should review graphs with asymptotes to get a more complete picture of this.

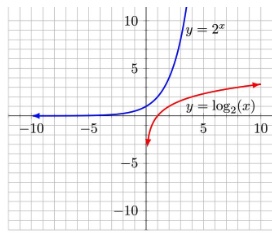
Exponential and Logarithmic Functions

Graphs of exponential [\(f(x)=2^{x}\)] and logarithmic [\(f(x)=log_2(x)\)] functions are shown above. The exponential graph is at the upper left. Notice how in this case the exponential function starts almost horizontally and grows with an increasing slope. The logarithmic function starts almost vertically and grows with a decreasing slope. Also, the exponential graph has one asymptote (horizontal, in this case the x-axis), and the logarithmic graph has one asymptote (vertical, in this case the y-axis). The basic shapes of both graphs are consistent, but their directions and asymptotes will change depending on whether the coefficients or the x values are positive or negative.

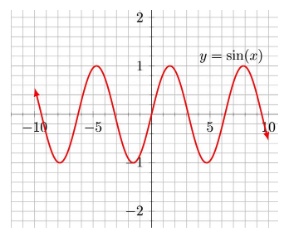
Trigonometric Functions

Graphs of trigonometric functions are periodic, meaning that they show a pattern that infinitely repeats itself, as the input values change positively or negatively. As the graph extends to the left and right, you can see how far a pattern goes before it starts to repeat itself. This portion of the domain is called the period of the function. For example when you graph \(f(x)=sin(x)\), as above, you will see a pattern that starts at \(x=0\) and starts to repeat at \(x=2\pi\ \approx (6.28)\). The period is \(2\pi\). The midline goes horizontally through the middle of the graph. In this case it is the x-axis. The amplitude is the height of the graph measured from the midline. In the sine graph above, the amplitude is 1. Be aware of the patterns in the other five trig functions as well as the sine.

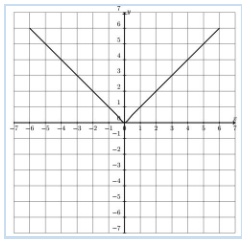
Other Functions and Ideas

Square root and cube root functions can usually be handled by just plotting a number of points. Piecewise functions are defined by dividing the domain into sections and using a different definition for each section. See the example below, which shows how to define an absolute value function in two pieces (as a piecewise function. The graph is shown above.

\[f(x) = |x| = \left\{ \begin{array}{lll} x & if & x\geq 0 \\ -x& if & x\lt 0 \\ \end{array} \right.\]