Geometric Theorems

Rigid transformations such as translations and rotations are key in being able to prove theorems about lines, angles, and geometric figures. Using the properties of symmetry should also be considered showing how sides for a given geometric figure are in proportion when they are dissected in particular ways.

Lines and Angles

It can be shown that vertical or opposite angles formed by two intersecting lines are congruent by rotating points on both lines about the point of intersection of the lines. In the image below, Points \(A\) and \(C\) rotated 180 degrees about point \(E\) to points \(B\) and \(D\) respectively. Distances have been preserved, therefore, \(\angle{AEC} \cong \angle{BED}\)

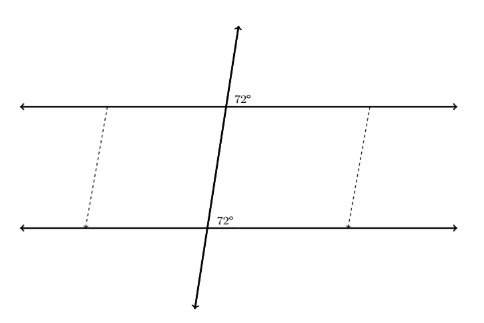
Alternate interior angles and corresponding angles can be shown to be congruent for two parallel lines cut by a transversal by translating one line along the transversal which preserves the angle measures formed by the parallel lines. (see figure below)

Triangles

You should be able to draw a line parallel to one side of a triangle through the other sides and note that it creates a similar triangle, thus cutting the sides proportionally. In this figure below, \(\overline{AC} \parallel \overline{ED}\), so \(\triangle{ACB} \sim \triangle{EDB}\) and \(\dfrac{AC}{ED} = \dfrac{BC}{BD} = \dfrac{BA}{BE}\).

Additionally, You can use similarity to prove statements such as the medians of a triangle meet at a point, and congruence to show the base angles of an isosceles triangle are congruent by CPCTC.

Parallelograms

You should also be able to decompose a parallelogram into two or more similar triangles in order to show congruence of sides and bisection of diagonals using proportionality statements or CPCTC. Remember that parallelograms with certain properties form rectangles, squares, or rhombuses.

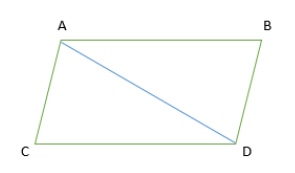
For instance: In the diagram below, for parallelogram \(ABCD\), \(\triangle{ABD} \cong \triangle{DCA}\)

Using Congruence and Similarity

You will also need to decompose multi-sided polygons, such as a pentagon and octagon, into multiple triangles that are similar or congruent in order to show those polygons have certain properties, such as all sides are congruent in a regular pentagon, or two octagons are congruent by CPCTC. Remember, a polygon can be decomposed into \(n-2\) triangles where \(n\) is the number of sides of the polygon. The figure below shows a pentagon that is decomposed into three triangles sharing a common vertex at \(A\).

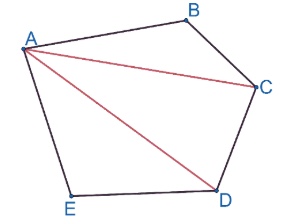
Pentagon \(ABCDE\) is decomposed into triangles \(\triangle{ABC}, \triangle{ACD},\) and \(\triangle{ADE}\).

Trigonometric Ratios

You will need to know how to solve right triangles (find any unknown angles and sides) using the trigonometric ratios for sine, cosine, and tangent as well as the Pythagorean Theorem.

Sine and Cosine

The prefix “co” in cosine means cosine is the complement to sine. Cosine and sine are complementary functions so, \(\cos(90^o-\theta) = \sin(\theta)\) and \(\sin(90^o - \theta) = \cos(\theta)\).

Pythagorean Theorem

You will need to know the trigonometric ratios. Remember the acronym SOHCAHTOA (Sine Opposite Hypotenuse Cosine Adjacent Hypotenuse Tangent Opposite **Adjacent) when determining which ratio is needed for a given situation. In the right triangle shown below, the opposite, adjacent sides are relevant to angle \(\theta\)

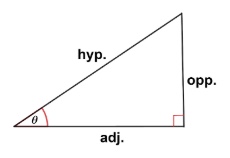
Remember: \(\sin(\theta) = \dfrac{\text{opp.}}{\text{hyp.}}, \cos(\theta) = \dfrac{\text{adj.}}{\text{hyp.}},\) and \(\tan{\theta} = \dfrac{\text{opp.}}{\text{adj.}}\).

If a triangle is similar to the one shown in the diagram shown, the trigonometric ratios are the same for angle \(\theta\) since the dilation transformation tells you the sides of the two triangles are proportional.

You will also need to be able to use ratios of the special right triangles, \(30-60-90\) and \(45-45-90\) to solve for missing sides and angles.

Coordinates

Much of what you probably learned in Algebra 1 will apply when using the coordinate system to show algebraically how some of the geometric theorems you will be asked to prove work. If you are asked to show find the perimeter or area of a geometric figure, or have to show similarity or congruence, make sure you know the formulas below. Note: This list is not exhaustive, but these formulas are standard when showing geometric relationships algebraically.

Slope of a line \(m = \dfrac{y_1 - y_2}{x_1 - x_2}\) where \((x_1, y_1)\) and \((x_2, y_2)\) are points on the line.

The equation of a line in slope-intercept form is \(y=mx+b\) where \(m =\) slope and \(b = y\)-intercept.

A line in point-slope form is \(y-y_1 = m(x-x_1)\), where \((x_1, y_1)\) is a given point on the line and \(m=\) slope.

Vertical lines have no slope and horizontal lines have zero for their slope.

Distance between two points: \(d=\sqrt{(x_1 - x_2)^2 + (y_1-y_2)^2}\) where \((x_1, y_1)\) and \((x_2, y_2)\) are the two points on the coordinate plane.

Midpoint formula: \((x_m, y_m) = \big(\dfrac{x_1+x_2}{2}, \dfrac{y_1 + y_2}{2}\big)\).

Volume Formulas

While you are probably familiar with perimeter and area, you will need to know how to find the volume of a 3-dimensional geometric shape. Make sure you know the volume formulas for spheres, prisms, cylinders, cones, and pyramids. You will need them to help you solve situational problems such as the volume of a swimming pool that has the shape of a rectangular prism for one-half and a triangular prism for its other half.

Geometric Constructions

While it is possible to make geometric constructions using a compass and a straight edge(ruler), you may have access to a computer graphics program to do so, Make sure you can construct the following: copy a given line segment, bisect a line segment, construct a perpendicular bisector of a line, and construct a line that is perpendicular to a given point that is not on a given line. Additionally, you will need to be able to copy an angle, and bisect an angle. These types of constructions can be used to draw other geometric figures such as a square or an equilateral triangle.

Circle Theorems

Make sure you know that the area of a sector of a circle is just a portion of the area of an entire circle. Think of it as a piece of pie where you knife cuts the pie through the center of the circle. Determine what portion of the pie you need to cut and multiply it by the entire area of the circle.

Also, make sure you know the arc length of a circle is the portion of the circle’s perimeter. In the area of a sector, arc length is a piece of the circumference of the circle. To find it, multiply what portion of the circumference you are asked to find by the circumference of the circle.

Conic Sections

You will need to know two of the conic sections that are constructed when a right circular cone is cut by a plane at a certain angle. The conic sections and the formulas are:

Parabola with vertex at point \((h,k)\) is \((x-h)^2 = 4p(y-k)\) if it opens up or down, or \((y-k)^2= 4p(x-h)\) if it opens left or right. \(p\) is the distance from the vertex to the directrix.

Circle centered at point \((h,k)\): \((x-h)^2 + (y-k)^2 = r^2\), where \(r\) is the radius.

Know how the parameters for the equations affect its shape and which way it opens or where its center will be, accordingly.

Relationships Between 2-D and 3-D Objects

Make sure you know that a 3-D objects’ sides are 2-D objects. The 2-D objects can be any of the polygons or circles. The lateral sides of the 3-D object are called faces and the top and bottom sides are called bases. The 3-D object is typically named by its base.

Modeling

You will need to be able to describe and estimate particular measurements for an object in a given situation using what you know about geometric figures and shapes such as parallelograms and prisms.

Shapes and Their Properties

You may need to know how to approximate the area, volume, or dimensions of a given object by comparing it with a known geometric figure that emulates the object’s shape.

Density

You may need to use a given density or ratio to determine the total amount for some substance. The density for a given material is the ratio of its mass and volume. For example, if a rectangular container with given dimensions in feet is filled with objects that weighs 13 oz. per cubic foot each, you can determine the total weight in ounces of the container by multiplying the volume of the container by the density of the object.

Solving Design Problems

You may need to be able to determine the dimensions that maximize the volume of a three-dimensional object that you construct from a given two-dimensional geometric figure. For example, if you cut squares from the corners of a given rectangular piece of material then fold the sides of the rectangular material upward to make a box with no top, what would be the length of the sides of the square corners you would need to cut that would maximize the volume of the open box?

Other Math Abilities Tested

Find discussion of other math abilities on this test here at the end of the last page of our SBAC High School Mathematics: Numbers and Operations Study Guide This information details other areas of math for which you will be responsible.

Tackling Differently Formatted Test Items

There is important information about differently formatted test items on the SBAC exam. Go to our home page for the SBAC to read it as you prepare. Scroll down to “Tips and Tricks.”