Mathematics Study Guide for the HiSET Test

Algebraic Concepts

Algebra is one of the broad parts of mathematics, together with number theory, geometry and analysis. In its most general form, algebra is the study of mathematical symbols and the rules for manipulating these symbols; it is a unifying thread of almost all of mathematics.

Expressions

An algebraic expression is a symbol or group of symbols used to represent a number or value. Expressions consist of one or more terms. Terms are separated by a $+$ or a $-$ sign. In an expression such as $3{x^2}$, $3$ is called the coefficient, $x$ is the variable, and the $2$ is called the exponent.

We simplify algebraic expressions by combining like terms. Like terms have the same variables with the same exponents. For example, $5x{y^3}$ and $3{x^3}y$ are not like terms because, although they have the same variables, the variables do not have the same exponents. However, $7a{b^2}{c^4}$ and $12a{b^2}{c^4}$ are like terms.

Example:

Simplify the expression: $9a{b^2}{c^4} - 2a{b^3}{c^2} - 2a{b^2}{c^4} + 6a{b^3}{c^2} + a{b^2}{c^4}$

Answer: $8a{b^2}{c^4} + 4a{b^3}{c^2}$

Explanation:

Select the terms that are like terms and combine their coefficients. If a term does not have a coefficient, understand that the coefficient is actually $1.$

\[\begin{array}{c} 9a{b^2}{c^4} - 2a{b^3}{c^2} - 2a{b^2}{c^4} + 6a{b^3}{c^2} + a{b^2}{c^4}\\ (9a{b^2}{c^4} + a{b^2}{c^4} - 2a{b^2}{c^4}) + (6a{b^3}{c^2} - 2a{b^3}{c^2})\\ 8a{b^2}{c^4} + 4a{b^3}{c^2} \end{array}\]

Algebraic expressions commonly have factors when the terms involve multiplication. For example, the term $16{x^2}yz$ has a number of unique factors. They are $2,4,8,16,x,{x^2},y,\;{\rm{and}}\;z.$

Algebraic expressions are called polynomials and can have more than one term. Here is a list of the types and names of these polynomials.

\[\begin{array}{|c|c|c|} \hline \text{Polynomial} & \text{Name} \\ \hline {3{x^2}} & \text{one term - monomial} \\ \hline {5{y^3} - 6{y^2}} & \text{two terms - binomial} \\ \hline {{x^3} + 4{x^2} - 9} & \text{three terms - trinomial} \\ \hline {{y^4} + 3{y^2} - 6y + 17} & \text{polynomial with four terms, etc.} \\ \hline \end{array}\]

Operations

Algebra involves the four arithmetic functions, addition, subtraction, multiplication, and division of polynomials. Remember, when adding or subtracting polynomials, combine like terms.

Example 1:

Add: $(2{x^3} + 4{x^2} - 6x + 5) + (7{x^3} - 2{x^2} + 8x + 9)$

Answer: $9{x^3} + 2{x^2} + 2x + 14$

Explanation:

Add: $\begin{array}{c}\left( {2{x^3} + 4{x^2} - 6x + 5} \right) + \left( {7{x^3} - 2{x^2} + 8x + 9} \right)\\\left( {2{x^3} + 7{x^3}} \right) + \left( {4{x^2} - 2{x^2}} \right) + \left( { - 6x + 8x} \right) + \left( {5 + 9} \right)\\9{x^3} + 2{x^2} + 2x + 14\end{array}$

Example 2:

Subtract: $(2{x^3} + 4{x^2} - 6x + 5) - (7{x^3} - 2{x^2} + 8x + 9)$

Answer: $- 5{x^3} + 6{x^2} - 14x - 4$

Explanation:

Subtract: $\begin{array}{*{20}{c}}{\left( {2{x^3} + 4{x^2} - 6x + 5} \right) - \left( {7{x^3} - 2{x^2} + 8x + 9} \right)}\\{\left( {2{x^3} - 7{x^3}} \right) + \left( {4{x^2} - ( - 2{x^2})} \right) + \left( { - 6x - 8x} \right) + \left( {5 - 9} \right)}\\{ - 5{x^3} + 6{x^2} - 14x - 4}\end{array}$

When multiplying polynomials, multiply the coefficients and add the exponents for each variable.

Example 3:

Multiply: $3{x^2}(3{x^3}y + 2x{y^2})$

Answer: $9{x^5}y + 6{x^3}{y^2}$

Explanation:

Multiply:

\[\begin{array}{c}3{x^2}(3{x^3}y + 2x{y^2})\\3 \cdot 3 \cdot {x^{2 + 3}} \cdot y + 3 \cdot 2 \cdot {x^{2 + 1}} \cdot {y^2}\\9{x^5}y + 6{x^3}{y^2}\end{array}\]

When dividing polynomials, divide the coefficients and subtract the exponents in the denominator from the exponents in the numerator for each variable.

Example 3:

Divide: $\frac{{64{x^4}{y^3}{z^2} - 16{x^3}{y^2}{z^3} + 8{x^2}{y^2}z}}{{4xyz}}$

Answer: $16{x^3}{y^2}z - 4{x^2}y{z^2} + 2xy$

Explanation:

Divide:

\[\begin{array}{l}\frac{{64{x^4}{y^3}{z^2} - 16{x^3}{y^2}{z^3} + 8{x^2}{y^2}z}}{{4xyz}}\\\frac{{64{x^4}{y^3}{z^2}}}{{4xyz}} - \frac{{16{x^3}{y^2}{z^3}}}{{4xyz}} + \frac{{8{x^2}{y^2}z}}{{4xyz}}\\16{x^3}{y^2}z - 4{x^2}y{z^2} + 2xy\end{array}\]

Equivalent Expressions

Equivalent expressions are expressions that represent the same values when simplified.

Example:

Are these two expressions equivalent? $8\left( {t + 3} \right) - 10$ and $12t - 6 + 20 - 4t$

Answer: Yes

*Explanation:

Simplify both expressions. $\begin{array}{*{20}{c}}{8\left( {t + 3} \right) - 10\; =\;? \;= \;12t - 6 + 20 - 4t}\\{8t + 24 - 10 =\;?\; = 12t - 4t - 6 + 20}\\{8t + 14 = 8t + 14}\end{array}$

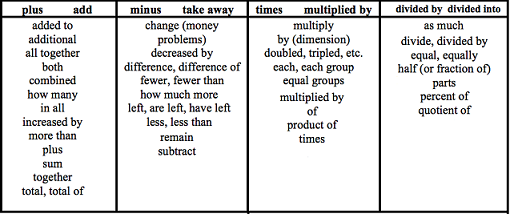
We often have to interpret expressions and write them using words. Be sure to study the keywords so you know what arithmetic operations are involved.

$key-math-words.-p-n-g$

Factoring Expressions

We can change the way expressions appear and make them easier to understand by factoring them. First, let’s factor a number into primes.

Example:

Factor $936$ into prime numbers.

Answer: ${{2^3} \cdot {3^3} \cdot 13}$

Explanation:

Using continuous division, $936$ is factored into primes:

\[\begin{array}{l}936 &=& 2 \cdot 468\\ &=& 2 \cdot 2 \cdot 234\\ &=& 2 \cdot 2 \cdot 2 \cdot 117\\ &=& 2 \cdot 2 \cdot 2 \cdot 3 \cdot 39\\ &=& 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 13\\ &=& {2^3} \cdot {3^2} \cdot 13\end{array}\]

Now, let’s factor out a greatest common factor (GCF). This factoring takes all of the common factors out of each term in a polynomial.

Example:

Factor the GCF out of $22x{y^2}{z^2} + 33{x^3}y{z^2} - 44{x^4}y{z^2}$

Answer: $11xy{z^2}\left( {2y + 3{x^2} - 4{x^3}} \right)$

Explanation: Identify the GCF and divide each term by it.

\[\begin{array}{c}22x{y^2}{z^2} + 33{x^3}y{z^2} - 44{x^4}y{z^2}\\11xy{z^2}\left( {\frac{{22x{y^2}{z^2}}}{{11xy{z^2}}} + \frac{{33{x^3}y{z^2}}}{{11xy{z^2}}} - \frac{{44{x^4}y{z^2}}}{{11xy{z^2}}}} \right)\\11xy{z^2}\left( {2y + 3{x^2} - 4{x^3}} \right)\end{array}\]

Now, we will factor quadratic trinomials of the form ${x^2} + bx + c.$ . In this factoring, factor the third term $c$ so the two factors multiply to give $c$ and add to give $b.$

Examples:

\[\begin{array}{l}{x^2} + 6x + 8 = (x + 2)(x + 4)\\{x^2} - 11x + 18 = (x - 2)(x - 9)\\{x^2} + 2x - 35 = (x + 7)(x - 5)\\{x^2} - 5x - 24 = (x - 8)(x + 3)\end{array}\]

Next, we will factor quadratic trinomials of the form $a{x^2} + bx + c.$ . In this factoring, factor the third term $c$ so the two factors multiply to give $c$ and add to give $b$, in conjunction with the factors of $a.$ When factoring this type of trinomial, be sure to check the answer using FOIL.

Examples:

\[\begin{array}{*{20}{c}}{3{y^2} - 7y - 6 = (3y + 2)(y - 3)}\\{2{h^2} + 7h - 15 = (2h - 3)(h + 5)}\\4{x^2} + 17xy - 15{y^2} = (4x - 3y)(x + 5y)\\4{r^2} + 8r + 3 = (2r + 1)(2r + 3)\end{array}\]

Now, let’s factor special quadratic expressions. The first one is a perfect square trinomial. This trinomial is the product of two identical binomials. The second one is called a difference of squares. This expression is the product of the sum and the difference of the square root of each term.

Examples:

\[\begin{array}{c}{x^2} + 6x + 9 = (x + 3)(x + 3) = {(x + 3)^2}\\25{v^2} - 20v + 4 = (5v - 2)(5v - 2) = {(5v - 2)^2}\\{r^2} - 4 = (r + 2)(r - 2)\\64{y^2} - 81 = (8y + 9)(8y - 9)\end{array}\]

Equations and Inequalities

Now, we will discuss solving linear equations and inequalities. Then, we will discuss solving polynomial equations by factoring and with the quadratic formula.

Solve inequalities the same way except when you multiply or divide both sides of the inequality by a negative number, you must reverse the direction of the inequality symbol. For example, $>$ changes to $<$, and $\ge$ changes to $\le.$

Linear Equations and Inequalities

The main idea when solving an equation is to isolate the variable, which means get the variable by itself on one side of the equation. Always remove parenthesis in an equation first. Isolate the variable by moving non-variable terms to one side using subtraction or addition, then move the variable terms to the other side using subtraction or addition, and lastly, isolate the variable using division or multiplication. Remember, move a positive term by subtracting it from both sides of the equation, and move a negative term by adding it to both sides of the equation.

Example 1:

Solve: $4(3 - m) = 2m + 24$

Answer: $m=-2$

Explanation:

\[\begin{array}{c}4(3 - m) &=& 2m + 24\\12 - 4m &=& 2m + 24\\ - 6m &=& 12\\m &=& - 2\end{array}\]

Now let’s solve a general linear equation, with letters as coefficients. Once we identify the variable, we solve these equations the same way as though the coefficients are numbers.

Example 2:

Solve for $x.$ $ax + by = c$

Answer: $x = - \frac{b}{a}y + \frac{c}{a}$

Explanation:

Remember, to solve for $x$ means to isolate the variable $x.$ Subtract $b$ from both sides of the equation. Then, divide both sides of the equations by $a.$

\[\begin{array}{c}ax + by &=& c\\ax &=& - by + c\\x &=& - \frac{b}{a}y + \frac{c}{a}\end{array}\]

Now, let’s solve an inequality:

Example 3:

Solve: $6(3 - x) \le 3x + 9$

Answer: $m \ge 1$

Explanation:

Notice that we have to divide both sides by $-9,$ so the inequality sign is reversed.

\[\begin{array}{c}6(3 - x) &\le& 3x + 9\\18 - 6x &\le& 3x + 9\\ - 9x &\le& - 9\\x &\ge& 1\end{array}\]

Quadratic Equations

One of the main purposes of factoring polynomials is to solve polynomial equations. When solving a polynomial equation, make sure the polynomial equals $0.$ Then factor the polynomial. Set each factor equal to $0$ and solve for the variables.

Examples:

\[\begin{array}{*{20}{c}}{{x^2} + 6x + 8 = 0;\;(x + 2)(x + 4) = 0;\;x + 2 = 0;\;x + 4 = 0;\;x = - 2, - 4}\\{{x^2} - 11x + 18 = 0;\;(x - 2)(x - 9) = 0;\;x - 2 = 0;\;x - 9 = 0;\;x = 2,9}\end{array}\] \[\begin{array}{*{20}{c}}{3{y^2} - 7y - 6 = 0;\;(3y + 2)(y - 3) = 0;\;3y + 2 = 0;\;y - 3 = 0;\;y = - \frac{2}{3},\;3}\\{2{h^2} + 7h - 15 = 0;\;(2h - 3)(h + 5) = 0;\;2h - 3 = 0;\;h + 5 = 0;\;h = \frac{3}{2},\; - 5}\end{array}\]

When a quadratic equation is difficult to factor or cannot be factored, we can solve it using the quadratic formula. For the equation $a{x^2} + bx + c = 0,$ the quadratic formula is:

\[x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}\]

The quadratic equation must equal $0.$

Example 1:

Solve using the quadratic formula: $15{x^2} + x – 28 = 0$

Answer: $x = - \frac{7}{5},\;\frac{4}{3}$

Explanation:

$15{x^2} + x – 28 = 0$; $a=15, b=1, c=-28$; $x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}$

\[\begin{array}{l}x = \frac{{ - 1 \pm \sqrt {{1^2} - 4 \cdot 15 \cdot - 28} }}{{2 \cdot 15}} = \frac{{ - 1 \pm \sqrt {1681} }}{{30}}\\x = \frac{{ - 1 \pm 41}}{{30}} = - \frac{{42}}{{30}}\;{\rm{or}}\;\frac{{40}}{{30}} = - \frac{7}{5}\;{\rm{or}}\;\frac{4}{3}\end{array}\]

Example 2:

Solve using the quadratic formula: $13{x^2} + 5x – 12 = 0$

Answer: $x = \frac{{ - 5 \pm \sqrt {{5^2} - 4 \cdot 13 \cdot - 12} }}{{2 \cdot 13}} = \frac{{ - 5 \pm \sqrt {649} }}{{26}}$

Explanation:

\[13{x^2} +5x – 128 = 0\] \[a=13\quad b=5 \quad c=-12\] \[x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}\] \[x = \frac{{ - 5 \pm \sqrt {{5^2} - 4 \cdot 13 \cdot - 12} }}{{2 \cdot 13}} = \frac{{ - 5 \pm \sqrt {649} }}{{26}}\]

Rational and Radical

If we solve an equation with rational terms, the first step is to multiply the entire equation by the Least Common Denominator (LCD) to remove the denominators from the equation. Then, we solve the equation like any other equation. This type of equation can have restrictions on the solution. No solution can make a denominator in the equation equal zero.

Example 1:

Solve: $\frac{1}{4}x + 1 = \frac{1}{2}$

Answer: $x=-2$

Explanation:

\[\begin{array}{c}\frac{1}{4}x + 1 &=& \frac{1}{2}\\4\left( {\frac{1}{4}x + 1} \right) &=& 4\left( {\frac{1}{2}} \right)\\x + 4 &=& 2\\x &=& - 2\end{array}\]

Example 2:

Solve:

\[x + \frac{2}{{x - 3}} = \frac{{x - 1}}{{x - 3}}\]

Answer: $x=1$

Explanation:

\[\begin{array}{c}x + \frac{2}{{x - 3}} = \frac{{x - 1}}{{x - 3}}\\(x - 3)\left( {x + \frac{2}{{x - 3}} = \frac{{x - 1}}{{x - 3}}} \right)\\{x^2} - 3x + 2 = x - 1\\{x^2} - 4x + 3 = 0\\(x - 3)(x - 1) = 0\\x = 3,\;1\\{\rm{Cannot}}\;{\rm{keep}}\;3\\x = 1\end{array}\]

Radical equations are equations that contain the variable inside a radical. When solving this type of equation, isolate the radical. Then, square the entire equation to eliminate a square root radical. If the equation contains a cube root, then you would cube the equation.

Example:

Solve this radical equation.

\[3x - 5\sqrt x = 2\]

Answer: $x = 4,\;\frac{1}{9}$

Explanation:

To solve the equation, isolate the radical with these steps: add $5\sqrt x$ to both sides of the equation and subtract $2$ from both sides of the equation. Then square the equation and solve the resulting quadratic equation using factoring, as shown here.

\[\begin{array}{r}3x - 5\sqrt x &=& 2\\3x - 2 &=& 5\sqrt x \\9{x^2} - 12x + 4 &=& 25x\\9{x^2} - 37x + 4 &=& 0\\(9x - 1)(x - 4) &=& 0\\x &=& \frac{1}{9},\;4\end{array}\]

Systems of Equations

A set of linear equations in the same two variables is called a system of linear equations, or linear system. Any ordered pair that is a solution to both equations in the system is a solution to the system of equations. This ordered pair is the point on the coordinate plane at which the two lines represented by the equations intersect.

Systems of linear equations can be solved algebraically using substitution or by using elimination. They can also be solved by graphing. If the equations represent parallel lines, then the system has no solution because the lines do not have an intersection point. If the equations represent intersecting lines, the system has one solution; the point at which the lines intersect. If the equations represent the same line, then the system has an infinite number of solutions because the line contains an infinite number of points.

Let’s solve a system using substitution. When we solve using substitution, we isolate one variable and then substitute the expression that that variable equals into the other equation. We then solve for the remaining variable. When we have solved for that variable, we substitute the value into one of the equations to find the value of the second variable.

Example:

Solve this system using substitution:

\[\begin{array}{r}x - 2y &=& 5\\4x + 3y &=& 9\end{array}\]

Answer: $(3, - 1)$

Explanation:

From the first equation, substitute $x=2y+5$ into the second equation.

\[\begin{array}{c}x - 2y &=& 5\\4x + 3y &=& 9\\4(2y + 5) + 3y &=& 9\\8y + 20 + 3y &=& 9\\11y &=& - 11\\y &=& - 1\\x &=& 2( - 1) + 5\\x &=& 3\end{array}\]

Now, we will solve a system using elimination. When we use this method, we create opposite coefficients for one of the variables. Then we add the two equations together to eliminate that variable. We solve the remaining variable. When we have solved for that variable, we substitute the value into one of the equations to find the value of the second variable.

Example:

Solve this system using elimination:

\[\begin{array}{c}4x + 3y = 5\\2x - 5y = - 17\end{array}\]

Answer: $(-1, 3)$

Explanation:

From the first equation, substitute $x=2y+5$ into the second equation.

\[\begin{array}{c}4x + 3y = 5\\2x - 5y = - 17\\\\4x + 3y = 5\\ - 2(2x - 5y = - 17)\\\\4x + 3y = 5\\ - 4x + 10y = 34\\\\13y = 39\\y = 3\\\\4x + 3(3) = 5\\4x + 9 = 5\\4x = - 4\\x = - 1\end{array}\]

Creating Equations and Inequalities

We use equations and inequalities to solve real-world problems. We read and understand the problem, formulate a model, solve the model, and verify the answer. Here are some examples of real-world problems we can solve using an equation.

Example 1:

Tickets to the Downtown Auditorium for a music concert cost $\$38$ for front section tickets and $\$28$ for back section tickets. There are 500 more back section seats than front row seats. If total ticket sales is $\$60,200.00$, how many seats are in the auditorium?

Answer: $2400$

Explanation:

Write an equation, choosing $x$ as the variable representing number of front section tickets. Then, $x+500$ is the expression representing the number of back section tickets. The total ticket sales for front section tickets are $38x.$ The equation is:

\[38x+28(x+500)=60,200\]

Solve this equation:

\[\begin{array}{r}38x + 28\left( {x + 500} \right) &=& 60,200\\38x + 28x + 14,000 &=& 60,200\\66x &=& 46,200\\x &=& 700\\x + 500 &=& 1200\\Total\;Seats\; &=& \;1900\end{array}\]

Example 2:

A piece of wire that is $150$ feet long is cut into three pieces of different lengths. The middle length piece is twice the length of the shortest piece. The longest length piece is three times the length of the shortest piece. How long is each piece?

Answer: $25$ feet, $50$ feet, and $75$ feet

Explanation:

Write an equation, choosing $x$ be the length of the shortest piece. Then, $2x$ is the length of the second piece, and $3x$ is the length of the longest piece. The sum of these three lengths must be $150.$ The equation is:

\[x + 2x + 3x = 150\]

Solve this equation.

\[\begin{array}{r}x + 2x + 3x = 150\\6x = 150\\x = 25\\2x = 50\\3x = 75\end{array}\]

The shortest piece is $25$ feet long, the second piece is $50$ feet long, and the longest piece is $75$ feet long.

Rearranging Formulas and Equations

Sometimes we are given an equation that represents a formula and we need to isolate a specific variable in that formula. Performing this operation is exactly the same as solving an equation using that variable as the variable of interest. Let’s solve some formulas for a specific variable.

Example 1:

Given the formula: $V = \frac{1}{3}{\pi ^2}h,$ solve for $r.$

Answer: $r = \sqrt {\frac{{3V}}{{\pi h}}}$

Explanation:

To solve for $r$, multiply both sides by $3.$ Then, divide both sides by $\pi h.$ Lastly, take the square root of both sides.

\[\begin{array}{c}V &=& \frac{1}{3}\pi {r^2}h\\3V &=& \pi {r^2}h\\\frac{{3V}}{{\pi h}} &=& {r^2}\\\sqrt {\frac{{3V}}{{\pi h}}} &=& r\end{array}\]

Example 2:

Given the formula: $P = 2(l+w),$ solve for $w.$

Answer: $w = \frac{p}{2} - l$

Explanation:

To solve for $w$, divide both sides by $2.$ Then, subtract $l$ from both sides.

\[\begin{array}{c}p &=& 2(l + w)\\\frac{p}{2} &=& l + w\\\frac{p}{2} - l &=& w\end{array}\]