Mathematics Study Guide for the HiSET Test

More Geometry Ideas

Circles

A circle is a set of points on a plane a given distance (called the radius) from a given point (called the center). This set of points is the circumference. The longest distance across a circle is the diameter. A chord is a line whose endpoints are both on the circle.

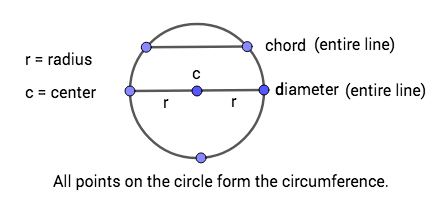
In mathematics, we typically work with circles on the coordinate plane. The formula for a circle with its center at the origin \(\left( {0,0} \right)\) is \({x^2} + {y^2} = {r^2}\) where \(r\) is the length of the radius.

Example:

What is the equation of the circle, whose center is at the origin and has a radius of \(6?\)

Answer: \({x^2} + {y^2} = 36\)

When the center is not on the origin, but is on the point \(\left( {h,k} \right),\) the equation of the circle is \({\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}\)

Example:

What is the equation of a circle whose center is at the point \(\left( {3,2} \right),\) and whose radius is \(5?\)

Answer: \({\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} = 25\)

Measuring Circles

Circles have the following properties.

The length of the diameter is twice the length of the radius, so \(d = 2r\)

The distance around a circle is called its circumference. The formulas for the circumference are: \(C = \pi d\;{\rm{or}}\;C = 2\pi r\)

Example 1:

What is the circumference of a circle whose radius is \(7\) inches? Use \(\bf{\pi = 3.14}\) in your calculations.

Answer: \(43.96\) inches

Explanation: \(C = 2(3.14)(7) = 43.96\)

Example 2:

What is the exact circumference of a circle whose radius is \(4\) inches?

Answer: \(8\pi\) inches

Explanation: \(C = 2(\pi)(4) = 8\pi\)

The area of a circle is calculated using the formula: \(A = \pi {r^2}.\) Once again, a question could tell you to use \(\pi = 3.14\) or to provide an exact answer.

Example:

What is the area of a circle with a radius of \(5.6\) feet? Use \(\pi = 3.14\) in your calculations. Do not round your answer.

Answer: \(98.4704\) square inches

Explanation: \(A = (3.14){(5.6)^2} = 98.4704\)

Arcs and Sectors

An arc of a circle is the portion of the circumference of the circle formed by two intersecting radii. A major arc is an arc that measures more than \(180^\circ.\) A minor arc is an arc that measures less than \(180^\circ.\) A sector of a circle is the region inside the circle (a portion of the circle) formed by two intersecting radii.

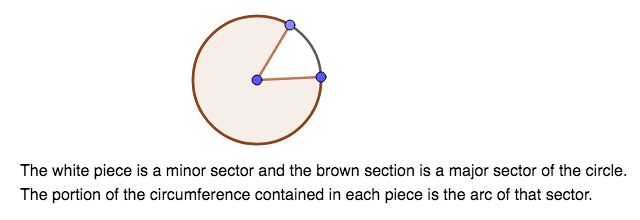
To find the area of an arc, we need to know the degree measure of the arc and the radius or circumference of the circle. Recall that a circle contains \(360^\circ.\) Thus, an arc is a portion of the \(360^\circ.\) When performing this type of operation, it is important to use the correct value of \(\pi\) because rounding can be different depending on which representation of \(\pi\) we use.

Example:

Find the length of an arc measuring \(75^\circ\) in a circle with a radius of \(9\) inches. Round your answer to the nearest two decimal places.

Answer: \(11.78\) inches

Explanation:

Make a fraction of the portion of the circle and multiply by the circumference.

\(\frac{{75}}{{360}}(2)(3.14)(9) = 11.775\) Round as requested.

We find the area of a sector in a similar way. The degree measurement of the sector is a portion of the whole circle’s \(360^\circ.\) Thus, a sector is the portion of the area of a circle. Again, when performing this type of operation, it is important to use the correct value of \(\pi\) because rounding can be different depending on which representation of \(\pi\) we use.

Example:

Find the area of a sector measuring \(75^\circ\) in a circle with a radius of \(9\) inches. Round your answer to the nearest two decimal places.

Answer: \(52.99\) square inches

Explanation:

Make a fraction of the portion of the circle and multiply by the area of the circle.

\(\frac{{75}}{{360}}(3.14)(9^2) = 52.9875\) Round as requested.

Notice \(\frac{{75}}{{360}}(\pi )({9^2}) = 53.014376,\) which is a slightly different answer.

Inscribed Angles

An inscribed angle is an angle whose vertex is on a circle and whose sides contain chords of the circle. The measure of an inscribed angle is exactly one-half of the arc it intercepts on the circle. If the measure of the inscribed angle is greater than \(90^\circ\), then the arc formed is a major arc. If the measure of the inscribed angle is less than \(90^\circ\), then the arc formed is a minor arc.

To find the measure of an arc, double the measure of the inscribed angle. To find the measure of the inscribed angle, divide the measure of the arc by two.

Pythagorean Theorem

The Pythagorean Theorem states that, in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs. We typically denote the legs as \(a\) and \(b\), and the hypotenuse as \(c.\) The theorem gives us the equation: \({a^2} + {b^2} = {c^2}\) When using this formula, enter the values given. Then, the last step is to square root the result.

Example:

Find the hypotenuse of a right triangle if the lengths of the legs are \(5\) and \(12.\)

Answer: \(13\)

Explanation:

\[\begin{array}{r}{5^2} + {12^2} &=& {c^2}\\15 + 144 &=& {c^2}\\169 &=& {c^2}\\\sqrt {169} &=& c\\13 &=& c\end{array}\]

We can also use the Pythagorean Theorem to determine if three segments would make a right triangle. If the three sides do not create an equality, when entered into the Pythagorean Theorem, then the sides would not make a right triangle. Please remember that the longest segment is the hypotenuse.

Example:

Would the three segments: \(9,39,41\) create a right triangle?

Answer: No

Explanation: \(41\) is the hypotenuse.

\[{9^2} + {39^2} = 81 + 1521 = 1602;\;{41^2} = 1681;\;1602 \ne 1681\]

Transformations

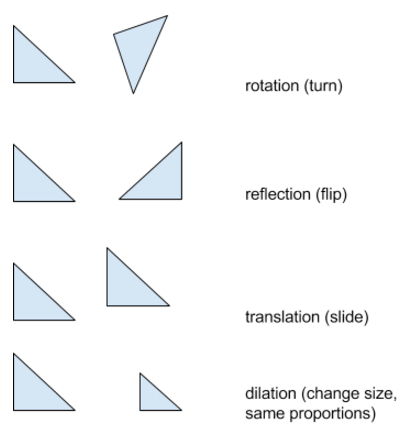
A transformation is a movement of an object. This movement can be left, right, up, down, or at an angle. The movement can be a reflection across an axis or across a line. We could rotate the object as specific angle or around a point either inside the object or outside the object. Lastly, we can dilate the object, making it bigger or smaller. We will look at each type of transformation.

Reflections

A reflection can be viewed as a flip movement. If we reflect an object across the \(x\)-axis, we change the sign of the \(y\)-coordinates of the object. If we reflect an object across the \(y\)-axis, we change the sign of the \(y\)-coordinates of the object.

Example:

Reflect a quadrilateral with these vertices \(\left( {1,3} \right),\;\left( {3,3} \right),\;\left( {4,5} \right)\;{\rm{and}}\;\left( {6,5} \right)\) about the \(y\)-axis. What are the new vertices?

Answer: \(\left( { - 1,3} \right),\;\left( { - 3,3} \right),\;\left( { - 4,5} \right)\;{\rm{and}}\; - \left( {6,5} \right)\)

Explanation:

Since we are reflecting about the \(y\)-axis, we will change the sign of the \(x\)-coordinate in each point. \(\left( {1,3} \right),\;\left( {3,3} \right),\;\left( {4,5} \right)\;{\rm{and}}\;\left( {6,5} \right) \to \left( { - 1,3} \right),\;\left( { - 3,3} \right),\;\left( { - 4,5} \right)\;{\rm{and}}\; \left( {- 6,5} \right)\)

Translations

A translation is a sliding movement of an object. This movement can be left, right, up, down, or at an angle. If we are dealing with an object on the coordinate plane, all corresponding points must move the same way. If we translate to the right or upward, we add to the \(x\)-value or \(y\)-value, respectively. If we translate to the left or downward, we subtract from the \(x\)-value or \(y\)-value, respectively.

Example:

Suppose a triangle on the coordinate plane with vertices \(\left( {1,3} \right),\;\left( {5,2} \right),\;{\rm{and}}\;\left( {2,4} \right)\) is translated \(3\) units upward and \(6\) units to the right. What are the new vertices?

Answer: \(\left( {7,6} \right),\;\left( {11,5} \right),\;{\rm{and}}\;\left( {8,7} \right)\)

Explanation: If we translate the figure \(3\) units upward, we must add \(3\) units to each \(y\)-value. If we translate the figure \(6\) units to the right, we must add \(6\) units to each \(x\)-value.

\[\left( {1 + 6,3 + 3} \right),\;\left( {5 + 6,2 + 3} \right),\;{\rm{and}}\;\left( {2 + 6,4 + 3} \right)\]

The new vertices are: \(\left( {7,6} \right),\;\left( {11,5} \right),\;{\rm{and}}\;\left( {8,7} \right)\)

Rotations

Rotations can be very complicated, are driven by formulas, and are mainly reserved for college-level courses. Rotating just means turning. In this section, we will consider rotating horizontal or vertical segments at right angles.

If we rotate a horizontal line to become a vertical line, the \(x\)-value in the point being rotated does not change and the \(x\)-value in the other point becomes the same as in this point. The \(y\)-value changes, but the length must remain the same. Since the original line was horizontal, the length of the line can be determined by the difference in the \(x\)-values in the points.

Example 1:

Rotate the horizontal segment with endpoints \(\left( {8,2} \right)\;{\rm{and}}\;\left( {14,2} \right)\) counterclockwise with the point \(\left( {8,2} \right)\) as the center of rotation. What are the new endpoints?

Answer: \(\left( {8,8} \right)\)

Explanation:

The point \(\left( {8,2} \right)\) is the center of rotation, so it does not change. The point \(\left( {14,2} \right)\) now has the same \(x\)-value as the other point and the \(y\)-value must be \(6\) units above the point of rotation. This endpoint is \(\left( {8,8} \right).\)

Example 2:

Rotate the vertical segment with endpoints \(\left( {2,2} \right)\;{\rm{and}}\;\left( {2,15} \right)\) clockwise with the point \(\left( {2,2} \right)\) as the center of rotation. What are the new endpoints?

Answer: \(\left( {15,2} \right)\)

Explanation:

The point \(\left( {2,2} \right)\) is the center of rotation, so it does not change. The point \(\left( {2,15} \right)\) now has the same \(y\)-value as the other point and the \(x\)-value must be \(13\) units to the right of the point of rotation. This endpoint is \(\left( {15,2} \right).\)

Dilations

Dilation is a transformation that either stretches or shrinks an object. If we dilate an object by a factor of \(3\), the values in the points of the object are multiplied by \(3.\) If we dilate an object by a factor of one-half, all of the values in the points of the object are divided by \(2.\)

Example 1:

An object with vertices \(\left( {0,0} \right),\;\left( {2,3} \right),\;{\rm{and}}\;\left( {4,5} \right)\) is dilated by a factor of \(4.\) What are the new vertices?

Answer: \(\left( {0,0} \right),\;\left( {8,12} \right),\;{\rm{and}}\;\left( {16,20} \right)\)

Explanation:

\[\left( {0,0} \right),\;\left( {2,3} \right),\;{\rm{and}}\;\left( {4,5} \right) \to \left( {0,0} \right),\;\left( {4 \cdot 2,4 \cdot 3} \right),\;{\rm{and}}\;\left( {4 \cdot 4,4 \cdot 5} \right) \to \left( {0,0} \right),\;\left( {8,12} \right),\;{\rm{and}}\;\left( {16,20} \right)\]

Example 2:

An object with vertices \(\left( {0,0} \right),\;\left( {2,6} \right),\;{\rm{and}}\;\left( {4,10} \right)\) is dilated by a factor of \(\frac{1}{2}\) What are the new vertices?

Answer: \(\left( {0,0} \right),\;\left( {1,3} \right),\;{\rm{and}}\;\left( {2,5} \right)\)

Explanation:

Divide all of the \(x\)-values and \(y\)-values by \(2.\)

Measuring Volume and Surface Area

In this section, we will discuss calculating the volume and surface area of special solids. We will use volume and surface area formulas.

Prism

A prism is a solid figure with parallel polygonal bases and parallel lateral edges. The lateral edges connect the bases and form the lateral area. The height or altitude of the prism is the distance between the bases.

The volume of the prism is the product of the area of the base (which depends on the polygon) and the altitude or height. The formula is \(V = Bh\) where \(V\) is volume, \(B\) is the area of the base, and \(h\) is the height or altitude of the prism.

Example:

Find the volume of a prism whose base is a square with sides \(6\) inches and whose height is \(15\) inches.

Answer: \(540\) cubic inches

Explanation:

\[\begin{array}{l}V &=& Bh\\V &=& ({6^2})(15)\\V &=& 540\end{array}\]

The surface area is the sum of all faces of the prism. Each base is a face and each part of the lateral surface is a face.

Example:

Find the surface area of a prism whose base is a square with sides \(6\) inches and whose height is \(15\) inches.

Answer: \(432\) square inches

Explanation:

\[\begin{array}{*{20}{l}}A& = &{2B + 4bh}\\A& = &{2({6^2}) + 4(6)(15)}\\V& = &{532}\end{array}\]

Cylinder

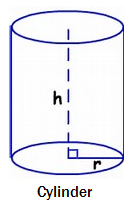
A cylinder is like a prism except that its bases are circles instead of polygons. In a right cylinder, the segment joining the centers of the circular bases is an altitude. The length of the altitude is called the height.

The volume of a cylinder is calculated using this formula: \(V = \pi {r^2}h\)

Example:

Find the volume of a cylinder whose base has a radius of \(3\) feet and whose height is \(8\) feet. Use \(\pi = 3.14\) in your calculations.

Answer: \(226.08\) cubic feet

Explanation:

\[\begin{array}{l}V &=& \pi {r^2}h\\V &=& (3.14)({3^2})(8)\\V &=& 226.08\end{array}\]

The surface area of a cylinder is found by adding the area of the top and bottom circular bases and the lateral surface area. The lateral surface area is found by multiplying the circumference of the circular base by the height. The formula for the surface area is: \(A = 2\pi {r^2} + 2\pi rh\)

Example:

Find the surface area of a cylinder whose base has a radius of \(3\) feet and whose height is \(8\) feet. Use \(\pi = 3.14\) in your calculations.

Answer: \(207.24\) square feet

Explanation:

\[\begin{array}{l}A &=& 2\pi {r^2} + 2\pi rh\\A &=& 2(3.14)({3^2}) + 2(3.14)(3)(8)\\A &=& 56.52 + 150.72\\A &=& 207.24\end{array}\]

Pyramid

A pyramid is like a prism, but one base is a point. Therefore, the lateral edges are not parallel to each other like in a prism but come to a point called the vertex of the pyramid. The distance from the base to the vertex is the height of the pyramid. The length of one side of the base is usually denoted as \(b.\)

The volume of a pyramid is one-third the area of the base times the height of the pyramid.

Example:

Find the volume of a square pyramid whose length of one side of the base is \(7\) meters and whose height is \(12\) meters.

Answer: \(196\) cubic meters

Explanation:

\[\begin{array}{l}V &=& \frac{1}{3}Bh\\V &=& \frac{1}{3}({7^2})(12)\\V &=& 196\end{array}\]

The surface area of a pyramid is the sum of the area of the base and the area of the lateral surfaces. To find the area of the lateral surfaces, we need the slant height, which can readily be calculated using the Pythagorean Theorem if it is not given.

Example:

Find the surface area of a square pyramid whose length of one side of the base is \(7\) meters and whose height is \(12\) meters, and whose slant height is \(12.5\) meters.

Answer: \(224\) square meters

Explanation:

\[\begin{array}{*{20}{l}}A& = &{{7^2} + 4\left( {\frac{1}{2}} \right)(7)(12.5)}\\A& = &{49 + 175}\\A& = &{224}\end{array}\]

Cone

A cone is like a cylinder, but one base is a point and the other is a circle. Therefore, there are no lateral edges. The distance from the base to the vertex is the height of the cone.

The formula for the volume of a cone is very similar to the formula for the volume of a pyramid, except that the base is a circle: \(V = \frac{1}{3}\pi {r^2}h\)

Example:

Find the volume of a cone whose base radius is \(8\) yards and whose height is \(15\) yards. Use \(\pi = 3.14\) in your calculations.

Answer: \(1004.8\) cubic yards

Explanation:

\[\begin{array}{l}V &=& \frac{1}{3}\pi {r^2}h\\V &=& \frac{1}{3}(3.14)({8^2})(15)\\V &=& 1004.8\end{array}\]

The surface area of a cone is the sum of the area of the circular base and the area of the lateral surface. The area of the lateral surface of the cone equals half the circumference of the base times the slant height of the cone. We can calculate the slant height using the Pythagorean Theorem if it is not given. The surface area is calculated using the formula: \(A = \pi {r^2} + \frac{1}{2}\left( {2\pi rl} \right)\;{\rm{or}}\;A = \pi {r^2} + \pi rl\) where \(l\) is the slant height.

Example:

Find the surface area of a cone whose base radius is \(8\) yards and whose height is \(15\) yards, and whose slant height is \(15.524\) yards. Use \(\pi = 3.14\) in your calculations. Round your answer to the nearest two decimals.

Answer: \(590.92\) square yards

Explanation:

\[\begin{array}{l}A &=& \pi {r^2} + \pi rl\\A &=& (3.14)({8^2}) + (3.14)(8)(15.524)\\A &=& 200.96 + 389.96288\\A &=& 590.92288\end{array}\]

Sphere

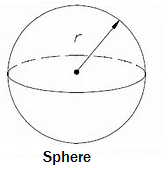
A sphere is the set of all points in space that are a given distance from a given point. The point is called the center and the distance is called the radius.

The volume of a sphere is calculated using the formula: \(V = \frac{4}{3}\pi {r^3}\)

Example:

Find the volume of a sphere whose radius is \(6\) centimeters. Use \(\pi = 3.14\) in your calculations.

Answer: \(904.32\) cubic centimeters

Explanation:

\[\begin{array}{l}V &=& \frac{4}{3}\pi {r^3}\\V &=& \frac{4}{3}(3.14)({6^3})\\V &=& 904.32\end{array}\]

The surface area of a sphere is calculated using the formula: \(A = 4\pi {r^2}\)

Example:

Find the surface area of a sphere whose radius is \(6\) centimeters. Use \(\pi = 3.14\) in your calculations.

Answer: \(452.16\) square centimeters

Explanation:

\[\begin{array}{*{20}{l}} A& = &{4\pi {r^2}}\\A& = &{4(3.14)({6^2})}\\A& = &{452.16}\end{array}\]

Density

A material’s density is defined as its mass per unit volume. It is, essentially, a measurement of how tightly matter is crammed together. Use the following formula for calculating density: \({\rm{Density}}\;\left( \rho \right) = {\rm{Mass}}\;(m)\;/\;{\rm{Volume}}\;(V)\)

Example 1:

A rectangular prism, with dimensions \(2\;cm \times 8\;cm \times 12\;cm\) is filled with a uniformly distributed material. If the material has a mass of \(1152\) grams, what is its density?

Answer: \(6\) grams per cubic centimeter

Explanation:

\[\begin{array}{l}\rho &=& \frac{m}{V}\\\rho &=& \frac{{1152\;g}}{{192\;c{m^3}}}\\\rho &=& 6\;g/c{m^3}\end{array}\]

Example 2:

A beaker with a volume of \(250\) cubic centimeters is filled with a uniformly distributed material. If the material has a density of \(7.3\;g/c{m^3}\) grams, what is its mass?

Answer: \(18252\) grams

Explanation:

\[\begin{array}{r}\rho &=& \frac{m}{V}\\7.3\;g/c{m^3} &=& \frac{m}{{250\;c{m^3}}}\\7.3\;g/c{m^3}\; \cdot \;250\;c{m^3} &=& m\\1825\;g &=& m\end{array}\]

Example 3:

Suppose a town, with an area of \(24\) square miles, has a population of \(1848.\) What is the average population density per square mile?

Answer: \(77\) people per square mile

Explanation:

To find population density, divide the population of the town by the area of the town. \(1848 \div 24 = 77\)

Example 4:

Suppose members of the Department of Natural Resources are estimating the deer population in a national forest. The forest lies along a \(25\) mile stretch of a certain interstate highway. They estimate that there are \(60\) deer living within a mile of the highway, \(240\) deer living between one mile and five miles from the highway, and \(900\) deer living between five miles and fifteen miles from the highway. What is the average deer population density per square mile in the national forest?

Answer: \(3\) deer per square mile

Explanation:

To find the deer population density, divide the deer population in the forest by the area of the forest. Based on the estimates, the deer population is: \(60 + 240 + 900 = 1200.\) The area of the forest is \(25 \cdot 1 + 25 \cdot 5 + 25 \cdot 10 = 400\) square miles. \(1200 \div 400 = 3\)