Mathematics Study Guide for the HiSET Test

Measurement and Geometry

Geometry is a branch of mathematics concerned with questions of shape, size, relative position of figures, and the properties of space. A mathematician who works in the field of geometry is called a geometer. We use geometry every day in our lives. In this section, we will discuss the most common aspects of geometry.

Polygons

The word polygon means many angles. In geometry, a polygon is a closed plane figure formed by coplanar segments (called sides). Each segment intersects exactly two other segments, one at each endpoint. The intersection points are called vertices. No two segments with a common endpoint are collinear. The fewest number of sides of any polygon is three sides. The angles inside the polygon are called interior angles. The angles, if extending one side, on the outside of the polygon are called exterior angles. Following is a list of names of common polygons which are based on the number of sides.

\[\begin{array}{|c|c|c|c|c|c|c|} \hline \text{Sides} & \text{3} & \text{4} & \text{5} & \text{6} & \text{7} & \text{8} \\ \hline \text{Name} & \text{triangle} & \text{quadrilateral} & \text{pentagon} & \text{hexagon} & \text{heptagon} & \text{octagon} \\ \hline \end{array}\]

Measuring Polygons

In this section, we will discuss formulas for finding the area, perimeter, and angles of polygons.

We can discuss perimeter in a general case because the perimeter is the sum of all sides of the polygon. There are a few formulas, which we will discuss on a case-by-case basis.

Triangles—The formula for finding the area of a triangle is:

\(A = \frac{1}{2}bh\) where \(A\) is area, \(b\) is the length of the base, and \(h\) is the height of the triangle.

Example:

What is the area of a triangle with a base with length of \(14\) inches, and a height of \(12\) inches?

Answer: \(84\) square inches

Explanation: Using the formula, \(A = \frac{1}{2}bh,\;A = \frac{1}{2}(14)(12) = 84\)

The sum of the interior angles of all triangles is \(180^\circ .\)

Example:

Find the missing angle inside a triangle if the measure of one angle is \(88^\circ\) and the measure of a second angle is \(52^\circ.\)

Or, on a test, you might be given a visual prompt like this one and told to find the measurement of angle \(x\):

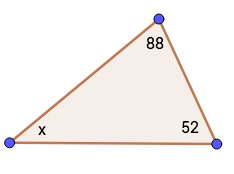
Answer: \(40^\circ\)

Explanation: \(180^\circ - 88^\circ - 52^\circ = 40^\circ\)

Quadrilaterals

Not all quadrilaterals have a formula for finding their area. However, the sum of the interior angles of all quadrilaterals, no matter what type, is \(360^\circ.\)

To find the area, use these formulas:

rectangle: \(A = bh\)

parallelogram: \(A = bh\)

square: \(A = {s^2}\) where \(s\) is the length of a side.

To find the perimeter, add all of the sides or use these formulas:

rectangle: \(P = 2l + 2w\) where \(P\) is the perimeter, \(l\) is the length, and \(h\) is the height.

square: \(P=4s\)

Regular Polygons With More Than Four Sides

A regular polygon is a polygon that has all angles with the same measure and all sides with the same length.

To find the perimeter, once again, add all of the lengths of the sides or multiply the length of one side by the number of sides.

To find the sum of the measures of the interior angles of a regular polygon, use this formula:

\(\text{Sum} = 180(n - 2)\), where \(n\) is the number of sides

Example:

What is the sum of the measures of the interior angles of a regular octagon?

Answer: \(1080^\circ\)

Explanation:

An octagon has \(8\) sides, so \(180(8 - 2) = 180(6) = 1080\)

To find the measure of an interior angle of a regular polygon, use this formula:

\(\text{Angle measure} = \frac{{180(n - 2)}}{n}\) where \(n\) is the number of sides

Example:

What is the measure of an interior angle of a regular hexagon?

Answer: \(120^\circ\)

Explanation:

A hexagon has \(6\) sides, so \(\frac{{180(6 - 2)}}{6} = \frac{{180(4)}}{6} = 120\)

Angles

An angle is the geometric shape formed when two rays begin at the same point, called the vertex. Each ray is called a side of the angle. Angles can be classified in several ways. One way is by their measure, as shown in the table below.

\[\begin{array}{|c|c|} \hline \text{Classification} & \text{Measure (m)} \\ \hline \text{acute angle} & \text{0 < m < 90} \\ \hline \text{right angle} & \text{m=90} \\ \hline \text{obtuse angle} & \text{90 < m < 180} \\ \hline \text{straight angle} & \text{m=180} \\ \hline \end{array}\]

Here is how these different angle types appear:

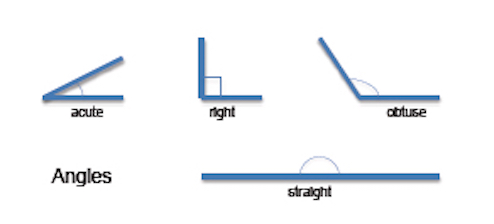
Angles can also be paired in special ways.

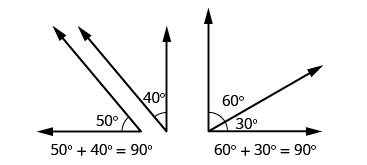
Complementary angles are two angles whose measures add up to \(90^\circ.\)

[This work is licensed by Rice University under a Creative Commons Attribution License (by 4.0).]

Supplementary angles are two angles whose measures add up to \(180^\circ.\)

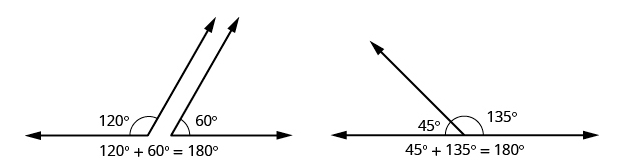
[This work is licensed by Rice University under a Creative Commons Attribution License (by 4.0).]

If we cut an angle in half, we bisect the angle. This means the angle is split into two equal smaller angles.

There are two types of angles inside a circle.

If the vertex is on the center of the circle, the angle is called a central angle. The measure of a central angle is the same as the measure of the arc it forms on the circle when the sides of the angle intersect the circle.

If the vertex is on the circumference of the circle, the angle is called an inscribed angle. The measure of an inscribed angle is one-half the measure of the arc it forms on the circle when the sides of the angle intersect the circle.

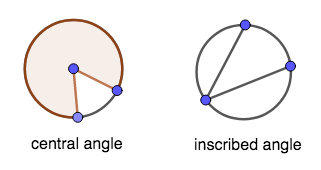
Triangles

Triangles are polygons with three sides called segments. We can determine if three segments could form a triangle using the concept that the sum of the lengths of the two shorter segments must be greater than the length of the longest segment.

Example 1:

Given three segments with lengths \(5\;in.,\;7\;in.,\;13\;in.\) Could these three segments form a triangle?

Answer: No

Explanation: The shorter sides; \(5\) and \(7\) add up to \(12,\) which is less than \(13\), the length of the longest segment.

Example 2:

Given three segments with lengths \(19\;in.,\;23\;in.,\;39\;in.\) Could these three segments form a triangle?

Answer: Yes

Explanation: The shorter sides; \(19\) and \(23\) add up to \(42,\) which is more than \(39\), the length of the longest segment.

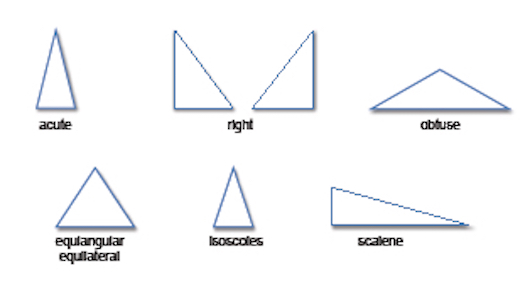
Types of Triangles

Triangles are classified by their angles:

Acute triangle: The measure of all angles is less than \(90^\circ.\)

Right triangle: The measure of one angle is \(90^\circ.\)

Obtuse triangle: The measure of one angle is greater than \(90^\circ.\)

Equiangular triangle: The measure of all three angles is \(60^\circ.\)

Triangles are also classified by the lengths of their sides:

Equilateral triangle: The lengths of all three sides are the same. (These triangles are also equiangular.)

Isosceles triangle: The lengths of two sides are the same. (The base angles of these triangles are also congruent.)

Scalene triangle: The lengths of each side are different. (The measure of each angle is also different.)

Measuring Triangles

The formula for finding the area of a triangle is:

\(A = \frac{1}{2}bh\) where \(A\) is area, \(b\) is the length of the base, and \(h\) is the height of the triangle.

Example:

What is the area of a triangle with a base with length of \(14\) inches, and a height of \(12\) inches?

Answer: \(84\) square inches

Explanation: Using the formula, \(A = \frac{1}{2}bh,\;A = \frac{1}{2}(14)(12) = 84\)

The sum of the interior angles of all triangles is \(180^\circ .\)

Example:

Find the missing angle inside a triangle if the measure of one angle is \(72^\circ\) and the measure of a second angle is \(59^\circ.\)

Answer: \(49^\circ\)

Symmetry

Some triangles have symmetry, which means we can draw a line of symmetry inside the triangle. The portion of the triangle on one side of the line of symmetry can be reflected across the line and match the portion of the triangle on the other side of the line of symmetry perfectly.

Equilateral triangle: There are three lines of symmetry, extending from each vertex to the midpoint of the opposite side.

Isosceles triangle: There is one line of symmetry, extending from the vertex angle that is unique to the midpoint of the side of the triangle between the congruent angles.

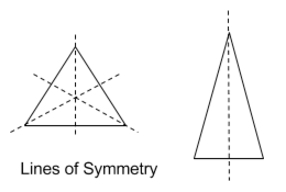
Other triangles do not have symmetry.

Congruency

If we say that two triangles are congruent, we are saying that the triangles have exactly the same size and shape. This means that corresponding sides in the two triangles are congruent and corresponding angles of the two triangles are congruent.

Let’s discuss the ways we can prove that two triangles are congruent:

Side-Side-Side (\(SSS\))

The \(SSS\) method of congruency is used when we know that corresponding sides in each triangle have the same length. For example, we can say:

\(\Delta ABC \cong \Delta DEF\) if and only if \(\overline {AB} \cong \overline {DE} ;\;\overline {BC} \cong \overline {EF} ;\;\overline {AC} \cong \overline {DF}\)

Side-Angle-Side (\(SAS\))

The \(SAS\) congruency method is used when we can show that two pairs of corresponding sides in each triangle are congruent and the angle between them in one triangle is congruent to the angle between them in the second triangle. For example, we can say:

\(\Delta ABC \cong \Delta DEF\) if \(\overline {AB} \cong \overline {DE} ;\;\overline {BC} \cong \overline {EF} ;\;\angle ABC \cong \angle DEF\)

Angle-Side-Angle (\(ASA\))

The \(ASA\) congruency method is used when we can show that two corresponding angles sides in each triangle are congruent and the side between them in one triangle is congruent to the side between them in the second triangle. For example, we can say:

\(\Delta ABC \cong \Delta DEF\) if \(\angle A \cong \angle D;\;\angle B \cong \angle E;\overline {AB} \cong \overline {DE}\)

Hypotenuse-Leg (\(HL\))

The \(HL\) congruency method is used to prove the congruence of right triangles. Since all right angles are congruent, the angle is not needed. This method originates from the Pythagorean Theorem, which given the length of the hypotenuse and one leg of the triangle, the other leg can only be a specific length.

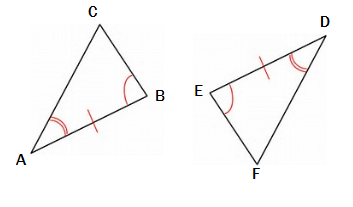
Example 1:

Is \(\Delta ABC \cong \Delta DEF?\) State the reason.

Answer: Yes, by the \(SAS\) congruency method.

Example 2:

Is \(\Delta ABC \cong \Delta DEF?\) State the reason.

Answer: Yes, by the \(ASA\) congruency method.

Example 3:

Is \(\Delta ABC \cong \Delta DEF?\) State the reason.

Answer: Yes, by the \(SSS\) congruency method.