Applied Mathematics Study Guide for the WorkKeys

Skills Needed for Level 6 Questions

Level 6 problems cover a lot of the same topics as earlier levels, but may take more steps or need more translation from word descriptions. Volumes of boxes will make an appearance.

More Work with Unlike Denominators

Example: A chemist needs to dilute some acid with water to make $1\dfrac{3}{4}$ liters of solution. If she has $\dfrac{2}{3}$ liter of acid, how much water does she need to add?

To find the amount needed, subtract the volume of acid from the final volume of the solution.

\[1\dfrac{3}{4}-\dfrac{2}{3}\] \[\dfrac{7}{4}-\dfrac{2}{3}\] \[\dfrac{7}{4}\times\dfrac{3}{3}-\dfrac{2}{3}\times\dfrac{4}{4}\] \[\dfrac{21}{12}-\dfrac{8}{12}\] \[\dfrac{13}{12}\text{ liters}\]

Reverse Percentages

A typical percentage problem would give a percentage increase or decrease and ask for the new amount. A reverse percentage problem is similar, but gives a percentage and the new amount, and asks for the original amount.

Example: A best selling book is marked down by $15 \%$ and is now selling for $\$25.50$. What was the original price?

We know the book was originally selling for $100 \%$ of its price. That means that after a $15 \%$ discount, the new price will be $85 \%$ of the original price. We can write this:

\[85 \% \text { of } \underline{\text{ Original Price}} = \$25.50\] \[0.85 \times \underline{ \text{Original Price}} = \$25.50\]

Now get the Original Price by dividing the $\$25.50 \text{ by } 0.85$.

\[\text {Original Price} = \dfrac {\$25.50}{0.85}\] \[\text {Original Price} = \$30.00\]

In a nutshell, for a decrease, subtract the percent decrease from $100$ and divide the new price by that percent, written as a decimal.

For an increase, add the percent increase to $100$ and divide the new price by that percent, written as a decimal.

More Unit Conversion

You should be able to convert units where multiple steps are needed, given equalities between units. An example would be converting from $1250$ mL to quarts, where $1$ fl. oz. $= 29.6$ mL and $1$ quart = $32$ fl. oz.

These are the possible conversion factors that could be made from the given information.

\[\dfrac{1 \text{ qt}}{32 \text{ fl. oz.}}\] \[\dfrac{32\text{ fl. oz.}}{1 \text{ qt}}\] \[\dfrac{1\text{ fl. oz.}}{29.6 \text{ mL}}\] \[\dfrac{29.6 \text { mL}}{1 \text{ fl. oz.}}\]

Starting with the given $1250$ mL, choose the factor that will cancel out mL and multiply that factor by the $1250$ mL.

\[\require{cancel} 1250 \cancel {\text{ mL}} \times \dfrac{1\text{ fl. oz.}}{29.6 \cancel{\text{ mL}}}=42.2 \text{ fl.oz.}\]

Now that you have converted to fl. oz., pick the factor that will cancel out fl. oz. and multiply that factor times the $42.2 \text{ fl.oz.}$

\[42.2 \cancel{\text{ fl.oz.}} \times \dfrac{1 \text{ qt}}{32 \cancel{\text{ fl. oz.}}}= 1.32 \text{qt.}\]

Finding Mistakes in Solutions

To figure out where a student mistake was made, you sometimes need to do the problem yourself. By looking at your steps and answer, you can often see where they went wrong and why.

A certain online computer file contains $5600$ MB (megabytes) of data, and it can be downloaded at a rate of $16$ MB per second. How many minutes will it take to download the file?

A student calculates that it will take $350$ minutes. What has he done wrong?

The student apparently did this calculation: $5600 \text{ MB} \times \dfrac{1 \text { sec.}}{16 \text{ MB}} = 350 \text { sec.}$.

This is a good way to do it, but he should have then converted 350 seconds to minutes.

Using the “Best Deal” in Calculations

Earlier in this guide, we found the best deal by finding the lowest ratio of cost to amount of product. This type of problem is a bit different, and you may be asked to use the best deal information in another calculation. Example:

Acme Rental Cars rents their cars for an initial fee of $\$100$ plus $\$38$ per day. Standard Rentals rents their cars for a flat rate of $\$45$ per day. How much money would you save by going with the best deal for a $14$-day rental?

This problem is easier than it may look. All you have to do is calculate the rental amount for $14$ days from each company.

Acme $100 + 14\times 38 = 632$
Standard $14\times 45=630$

It looks like Standard is cheaper by $\$2$.

More Work with Area

You should know how to use the common formulas for areas of geometric figures and be able to rearrange the formulas to solve for something other than area. There may be two-step problems where you use your calculated area to calculate something else, or you may need to convert measurement units.

Example: A circular golf green has a diameter of $18 \text{ m}$. If a greens mower can cut grass at a rate of $0.5 \frac{\text {m}^{2}}{\text{sec.}}$, how many minutes, to the nearest tenth, will it take to mow the green?

If the diameter is $18 \text{ m}$, the radius is $9 \text{ m}$.

$\text {Area}=\pi \text {r}^{2}$
$A=3.14\times 9^{2}$
$A=254 \text{ m}^{2}$

Now calculate the time needed.

\[\require{cancel} 254 \cancel{\text{ m}^{2}} \times \dfrac{1 \text{ sec.}}{0.5 \cancel{\text { m}^{2}}}\] \[508 \text{ sec.}\]

And change that to minutes.

\[\require{cancel} 508 \cancel{\text{ sec.}} \times \dfrac{1 \text{ min.}}{60 \cancel{\text { sec.}}}\] \[8.5 \text{ min.}\]

Volume of Rectangular Solids

Rectangular solids are basically boxes.They have length, width, and height. If all three dimensions are the same, they are called cubes, though, in spite of the name, ice cubes are not necessarily true cubes. Volumes are easy to find if you know the three dimensions; just multiply the three, getting cubic units for an answer.

Formula for a rectangular solid: $V=lwh$

And for a cube: $V=s^{3}$ where s is the length of an edge.

Example: Which would hold more water, a rectangular tank that is $30$ cm by $40$ cm by $50$ cm, or a cubic tank that is $40$ cm on edge?

Rectangular tank: $V = 30 \text{ cm} \times 40 \text{ cm} \times 50 \text{ cm} = 60,000 \text{ cm}^{3}$
Cubic tank: $V= (40 \text{ cm})^{3} = 64,000 \text{ cm}^{3}$

More Work with Rates

Common rates involve things like miles per hour or meters per second, but can also be about rates of flow (liters per minute) or rates of factory production (pencils per hour).

Calculating Rate

Remember, a rate is just a ratio, very often with time on the bottom, and usually simplified to a unit rate ($1$ unit on the bottom).

This rate

\[\dfrac{60 \text{ gallons}}{ 4 \text{ minutes} }\]

is not a unit rate, but it can be simplified (reduced) to

\[\dfrac{15 \text{ gallons}}{ \text{ minute} }\]

which is a unit rate. Unit rates have an understood $1$ on the bottom.

See the next section for an example.

Calculating Production Rate

Example: A stamping machine cranks out $1400$ jigsaw puzzles in an $8$-hour shift. What is the production rate in puzzles per hour?

Divide $1400$ by $8$.

\[\dfrac{1400 \text{ puzzles}}{ 8 \text{ hours} } = \dfrac{175 \text{ puzzles}}{ \text{ hour} }\]

This could also be written in text as $175$ puzzles per hour.

Matching Equations to Problems

These problems are pretty much just like they sound. A problem will be presented, and you will have a choice of several different equations to solve it. You can decide which equation is right by solving the problem yourself and comparing your method to the choices. Keep in mind that there is often more than one right way to solve a problem.

Example: What is the area of the figure below?

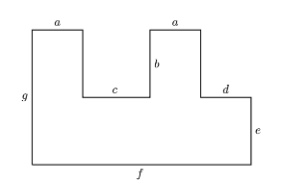
$A=ag+ag-bc$
$A=2ac + de$
$A=bc+bd+ag$
$A=fg-bc-bd$

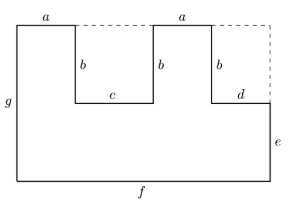
Add the dashed lines to make the drawing clearer, and add additional labels to show all the segments that have length $b$.

Write the area for the big overall rectangle: $fg$
Subtract the area of the rectangle that is $b \times c$: $bc$
Also subtract the area of the rectangle that is $b \times d$: $bd$
This gives you $fg-bc-bd$.