Applied Mathematics Study Guide for the WorkKeys

Skills Needed for Level 5 Questions

You will see problems in this level that require some higher order thinking skills, including working through several steps and sorting through given information to decide what may be irrelevant. Fractions are a little bit more complicated and a few basic geometry problems make an appearance.

Determining Useful Information

In Level 5 problems, much as in life, you may see extra information that you will need to ignore to solve the problem. The best way to handle that is to thoroughly understand the problem. Read it carefully three times. Write each given number down and label it. Be sure you understand what you are supposed to be finding.

Here’s a simple example. Suppose you go to the store and buy 2 cans of soup, 3 apples, a carton of orange juice, a head of lettuce, 3 cans of beans, a gallon of milk, and a 2-liter bottle of Coke. How many containers will you be taking home? (Shopping/produce bags don’t count.)

Clearly, you ignore the apples and lettuce and do this:

2 + 1 + 3 + 1 + 1 = 8

More Adding and Subtracting Fractions

What if you have to add or subtract fractions with different denominators? Then you have to change both fractions so they have the same denominator, called a common denominator.

The quickest way to get a common denominator is to simply multiply the two different denominators.

Example: $\dfrac{2}{3}+\dfrac{5}{8}$

A common denominator is $3 \times 8=24$

To make each fraction have this denominator, do this:

\[\dfrac{8}{8}\cdot \dfrac{2}{3} = \dfrac{16}{24}\] \[\dfrac{3}{3}\cdot \dfrac{5}{8} = \dfrac{15}{24}\]

Now you can add the two fractions. Remember to add just the top numbers.

\[\dfrac{16}{24}+\dfrac{15}{24}=\dfrac{31}{24}\]

Generally, you will want to change any improper fraction to a mixed number.

\[\dfrac{31}{24}=1\dfrac{7}{24}\]

You may very well have to reduce your final answer. Watch for that.

Note: There is a way to find the lowest common denominator, but you will never need it if you don’t mind reducing your answer.

Unit Conversion

A good way to convert between units is the conversion factor approach. A conversion factor is something that you multiply by to convert units, just like it sounds. Let’s use inches and feet to show how it’s done.

We know $12\text{ inches}=1\text{ foot}$. From this, we can make two different fractions.

$\dfrac{12\text{ in.}}{1\text{ ft.}}$ and $\dfrac{1\text{ ft.}}{12\text{ in.}}$

These are our conversion factors. Here is how they work.

Change $30\text{ in.}$ to $\text{ feet}$.

Put a $1$ under the $30\text{ in. }$ Use the second fraction above and multiply.

\[\frac {1 \text{ ft.}}{12\text{ in.}} \times \dfrac {30\text{ in. }}{1}\]

Notice how the inch units are in just the right positions to cancel out.

\[\frac {1 \text{ ft.}}{12{\require{cancel}\cancel { in.}}} \times \dfrac {30\cancel{in.} }{1}\]

That’s why we picked the second fraction, and that’s also how we know we picked the right fraction. Now we can write:

\[\frac {1 \text{ ft.}}{12{\require{cancel}\cancel { in.}}} \times \dfrac {30\cancel{in.} }{1}=\dfrac{30 \text{ ft.}}{12}\]

Simplified, that would be $2.5 \text{ ft.}$.

If we were changing feet to inches, we would have picked the first fraction to multiply by.

This method works for changing almost anything to something else. As long as you know equivalencies such as these, you can make conversion factors from them.

$1$ mile = $5280$ ft.
$1$ pound = $16$ ounces
$1$ kilogram = $2.2$ pounds
$1$ quart = $32$ fluid ounces
$1$ inch = $2.54$ cm

Operations with Mixed Units

Mixed units are measures that are split into two or more units. Examples would be a time of $2$ hours $50$ minutes or a height of $6$ feet $2$ inches. The basic idea to add or subtract them is to keep each unit in its own column and simplify the final result.

Example:

Add $3$ h $20$ min to $1$ h $50$ min.

\[\begin {array}{rr} 3\text{ h}&20\text{ min} \\ +1\text{ h}& +50 \text{ min}\\ \hline 4\text{ h}&70 \text { min}\\ \end{array}\]

Simplifying: If the number of minutes is over $60$, you should subtract $60$ from that number and add $1$ to the number of hours.

\[5\text{ h }10\text{ min}\]

Subtraction is very similar, though you may have to use “borrowing” (also known as “regrouping”) just as you do in the subtraction of single numbers. Here’s an example of the same two quantities as above, but doing subtraction

\[\begin {array}{rr} 3\text{ h}&20\text{ min} \\ -1\text{ h}& -50 \text{ min}\\ \hline 1\text{ h}&30\text{ min}\\ \end{array}\]

Borrow $1 \text{ h}$ from the $3 \text{ h}$ and add it, (as $60 \text{ min}$) to the $20 \text{ min}$. Then subtract.

\[\begin {array}{rr} 2\text{ h}&80\text{ min} \\ -1\text{ h}& -50 \text{ min}\\ \hline 1\text{ h}&30\text{ min}\\ \end{array}\]

Finding the “Best Deal”

Finding the best deal is sometimes a matter of finding the lowest ratio of cost to amount of product. Suppose you can get a $10$ oz. box of Crunchy Wheats for $\$2.29$ or a bigger $24$ oz. box for $\$4.95$. To find the best deal, calculate the cost-to-amount ratio for each box. The ratios here have been rounded to the nearest cent.

\[\dfrac{\$2.29}{10} = \dfrac{\$0.23}{1\text{ oz}}\] \[\dfrac{\$4.95}{24} = \dfrac{\$0.21}{1\text{ oz}}\]

The lowest cost per ounce is the better deal.

Geometric Calculations

You will need to know the basic geometric terms and calculations listed below. The calculations will need one or two steps.

Perimeter

The perimeter is the sum of all the sides of a geometric figure. Imagine an ant making a round trip around the sides of a figure. The distance it travels is the perimeter.

Suppose there is a rectangle with dimensions $2\times 8$ and a square that is $4 \times 4$. Which one has a larger perimeter?

Rectangle: $2+8+2+8=20$
Square: $4+4+4+4=16$
Rectangle wins.

Circumference

The circumference is the perimeter of a circle. Even though a circle has no line segments for sides that you can add up, it still has a distance that an ant can walk around. Because there are no segments to add up, you have to calculate the perimeter (circumference) using a formula, namely $\text{ C}=\pi \text{d}$ or $\text{ C}=2\pi \text{r}$.

Example: Find the circumference of a circle with a radius of $8.5$ cm.

\[\text{ C}=2\pi \text{r}\]

$\text{ C}\approx 2(3.14) (8.5\text{ cm})$
$\text{ C}\approx 53.4 \text{ cm}$

Area

You will have a formula sheet to use that will include areas of geometric figures that show up on the test. Still, it’s good to have a few common area formulas fresh in your mind, such as the following:

Rectangle: $A = lw$ where $l$ is the length and $w$ is the width
Square: $A=s^{2}$ where $s$ is the length of an edge
Triangle: $A=\frac{1}{2}bh$ where $b$ is the length of the base and $h$ is the height
Circle: $A=\pi r^{2}$

In Levels 6 and 7, you may need to do a two- or three-step problem like the following example.

If the radius of the big circle is $40$ cm and the radius of the small circle is $20$ cm, what is the area of the shaded region?

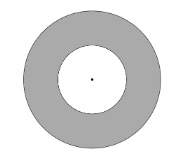
Find the area of the big circle and subtract the area of the small circle from it.

Big circle: $A=3.14 \times 40^{2}=5024 \text{ cm}^{2}$
Small circle: $A=3.14 \times 20^{2}=1256 \text{ cm}^{2}$

Shaded region: $5024 \text{ cm}^{2}-1256 \text{ cm}^{2}=3768 \text{ cm}^{2}$

More Percentage Calculations

These problems go a little further than basic percentage calculations. At this level of question, you will have to calculate a percentage, but then you will use that to calculate another quantity, such as a discount or sales tax. Example:

Max found some new shoes marked down from $\$85.00$ to $\$72.25$, but decided instead to buy some that were marked down from $\$98.00$. Assuming both pairs of shoes were marked down by the same percentage, how much did he pay for his shoes?

First, calculate the percentage discount on the first pair.

\[85.00 - 72.25 = 12.75\] \[\dfrac{12.75}{85.00}=0.15 = 15 \%\]

Now apply that discount to $\$98.00$.

\[0.15 \times 98.00 = 14.70\] \[98.00 - 14.70= 83.30\]

So Max paid $\$83.30$.

Finding Calculation Errors

Given a multi-step calculation with an error, find the line that has the error.

\[\begin {array}{cl} 18+3\times4-5(7-12)& \text{ Line 1}\\ 21\times4-5(7-12)& \text{ Line 2}\\ 84-5(-5)&\text{ Line 3}\\ 84+25&\text{ Line 4}\\ 109&\text{ Line 5}\\ \end{array}\]

Line $2$ has the error. Addition was done before multiplication, an order of operations error.