Mathematics: Geometric and Spatial Reasoning Study Guide for the TSIA2

Measuring Geometric Figures

Many math questions involving geometric concepts ask you to determine the measurements of geometric figures, both two- and three-dimensional. Knowing which formulas that apply to the problem is a big help.

Properties of Geometric Figures

First, let’s look at the different types of geometric figures and their unique qualities.

Polygons

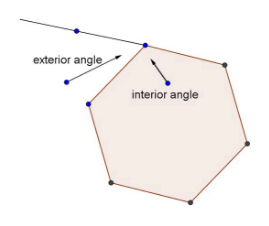
A polygon is a collection of points and line segments joining those points that encloses an area of the plane. The line segments cannot overlap. The polygon has an interior and exterior. The line segments are called the edges or sides of the polygon. In a regular polygon, all of the edges are equal in length.

Vertices

The points where the edges of the polygon meet are the vertices (plural of vertex).

Angles of a Polygon

• Each vertex of the polygon with the two adjacent segments forms an angle.
• The interior angles face the inside of the polygon.
• The exterior angles face the outside.

• The exterior angles add up to 360 degrees.

• In a regular polygon, all interior angles are equal.

Circles

A circle is a set of points equidistant from a given point. The given point is the center of the circle and the radius is the distance from the center to the points. Here are other characteristics:

Diameter — a straight line segment from one point on the circle through the center to another point on the circle. The diameter is twice the length of the radius.

Circumference — the distance around the circle starting at a point and returning to the same point. The formula for the circumference is \(C = 2 \pi r\) or \(C = \pi d\).

Area — the amount of two-dimensional space contained within the circle. The formula for the area is \(A = \pi r^{2}\).

Arc — the length along the circle between two points on the circle.

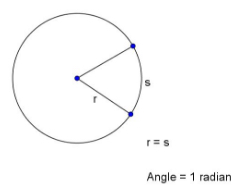
Radian — An angle drawn with the vertex at the center of a circle will intersect the circle at two points. When the length of arc between those points is equal to the radius, the angle that made that arc is one radian. There are \(2 \pi\) radians in a complete circle.

Triangles

Triangles are a special type of polygon with three sides. There are many special properties of triangles, even for those with unequal sides and angles.

Rectangles

Rectangles are four-sided polygons with opposite sides equal and all interior angles of 90 degrees. The longer side of a rectangle is commonly called the length and the shorter side is the width. If all four sides of a rectangle are equal (length = width) it is known as a square. A square is a regular rectangle.

Three-Dimensional Geometric Figures

Three-dimensional objects are composed of two-dimensional figures that are joined along their sides and extend into the third dimension. The 2-D figures are the faces, the lines joining them are the edges, and the points where edges meet are the vertices.

Measuring Perimeter

When you measure the perimeter of a figure, you are asked for the distance along the outside edge of that figure. Units of length, such as feet, inches, or meters, are used to express perimeter measurements.

Perimeter of Polygons

The perimeter of a polygon is the distance starting at a point on the polygon, going around, and returning to the same point. For a regular polygon with \(n\) sides and each side length \(s\), the perimeter is \(P = ns\).

Rectangles have a simple formula for determining perimeter:

For a rectangle of length \(l\) and width \(w\), the perimeter is \(P = 2l + 2w\).
For a square with side \(s\), \(P = 4s\).

Perimeter of Triangles

The perimeter of a triangle is equal to the sum of its sides. For an equilateral triangle of side \(s\), \(P = 3s\).

Perimeter of Circles

The perimeter of a circle is its circumference, as described above. Here’s a quick note about the formula used to find circumference. Do you remember that pi is defined to be the ratio of the circumference of a circle to its diameter? That gives us:

\[\pi = \dfrac{C}{d}\]

Now just multiply both sides by \(d\), and get the well known \(C=\pi d\).

Measuring Area

It’s easy to become confused between the terms perimeter and area in math questions, but be sure you know the difference. The calculations and formulas are very different. The area of a figure is the total amount of space contained within it. It is expressed in square units, such as square feet or \(\text{feet}^2\).

Area of Polygons

The area of a polygon is the amount of two-dimensional space contained inside the polygon. The formula for the area depends on the type of polygon.

To determine the area of a rectangle, use this formula:

For a rectangle of length \(l\) and width \(w\), the area is \(A =lw\).
For a square with side \(s\), \(A = s^{2}\).

Area of Circles

As mentioned earlier, the formula for the area of a circle is \(A=\pi r^2\), where \(A\) is the area and \(r\) is the radius. You may be asked for an area calculated, say, to the nearest tenth or hundredth of a unit. That’s when you will want to use \(\bf{\pi = 3.14}\) in your calculation. More decimal places are known for pi if you need more decimal places in your answer, but it would be unusual for that need to arise.

Area of Triangles

The height of a triangle is the length of a line segment from a vertex and perpendicular to the opposite side. That opposite side is called the base. The area of a triangle is \(A = \frac{1}{2} bh\).

Surface Area

The surface area of a three-dimensional figure is the sum of the areas of the individual two-dimensional faces that make up the 3-D figure.

Measuring Volume

The volume of a three-dimensional figure is the amount of space contained within the faces of the figure. If measures of length are used, volume can be expressed in \(\text{units}^3\).

There are some special three-dimensional objects that have specific formulas for volume measurement. Here are some facts about them.

Rectangular prism—A rectangular prism is a box-like figure whose faces are all rectangles and all the rectangles meet at 90-degree angles. If the sides of the rectangular prism have lengths of \(x\), \(y\), and \(z\), then the volume \(V = xyz\) and the surface area \(S = 2xy + 2xz + 2yz\).

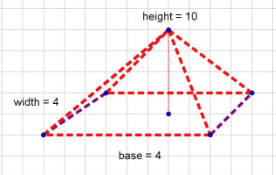
Rectangular pyramid—A rectangular pyramid has a rectangular base and four triangular sides that meet at a single vertex. The length of a line segment from this vertex perpendicular to the base is the height of the pyramid. If the rectangle has length \(l\) and width \(w\), and the height is \(h\), then the volume \(V = \frac{1}{3} lwh\). There is a complicated formula for the surface area that involves using the Pythagorean Theorem. It is best just to find the areas of the four triangles and add the area of the base \(lw\).

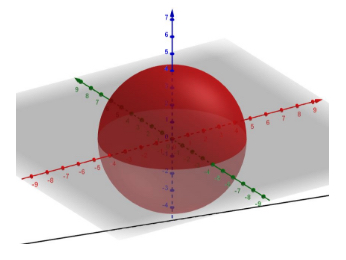
Sphere—A sphere is a set of points equidistant from a central point in three dimensions. It is a circle that has been rotated about its diameter in 3-D space. The distance from the center to the sphere is the radius. A sphere of radius \(r\) has a surface area \(S = 4 \pi r^{2}\) and a volume \(V = \frac{4}{3} \pi r^{3}\).

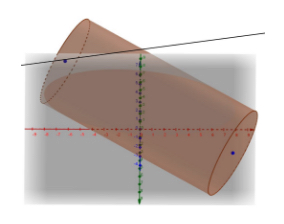
Cylinder—A cylinder resembles a can, or a circle extended into the third dimension (height). The top and bottom surfaces are circles. The side surface is a rectangle with a length equal to the circumference of either circle and a width equal to the height of the cylinder. For a cylinder with radius \(r\) and height \(h\), the volume \(V = \pi r^{2}h\) and the surface area \(S = 2 \pi r(h + r)\).

Estimating Measures

Estimating an answer can be a relatively quick way to see if your calculated result is in the ballpark. If the estimate doesn’t even come close to your result, it’s probably time to recheck your math.

Example

Suppose a rectangular solid has the dimensions \(22.3 \text{ cm} \times 38.7 \text{ cm} \times 91.0 \text{ cm}\). To estimate the volume of the solid, round off each dimension to the nearest ten cm and multiply them.

\(A = 20 \times 40 \times 90 = 2 \times 4 \times 9\) plus three zeros.

\[A = 72,000 \text{ cm}^3\]

Compare this with the more exact answer of \(78,533.91 \text{ cm}^3\)

The two results are not super close to each other, but they usually won’t be in estimating. It’s enough that they are roughly the same.