Mathematics: Levels E, M, D, and A Study Guide for the TABE Test

Number and Operations in Base Ten: Part 2

Percentage of Test Level Specifically Assessing Number and Operations in Base Ten (— = Assumed)

L	E	M	D	A
40%	28%	15%	—	—

Operations

As you have no doubt noticed in math, numbers are combined in different ways. These combinations are called operations. The common symbols $+, -, \times,$ and $\div$ are called operators and tell us what to do with the two numbers.

For example, in $13 \times 4$ the $\times$ symbol is the operator that tells us to use the operation multiply with $13$ and $4$.

Addition

Basic addition is the operation that combines two or more numbers into one (usually) larger number called the sum or total. You should be able to use column addition to add numbers from one digit to four digits as shown in the sections below. In a word problem, watch for the key words sum, total, added to, increased by, and plus to tell you that you’ll need to use addition.

Basic Adding in Columns

Adding whole numbers without the aid of a calculator is simplified by first writing the addends (the numbers to be added) vertically. Align digits according to their place value – ones at the first rightmost column, followed by the tens to the left, then hundreds, and so on. To add 1,045 and 34, write the addends vertically, carefully aligning the digits according to place value:

\[\begin{align} 1\text{,}045& \\ \underline{+\quad 34}& \\ \end{align}\]

Start adding from the ones column, going to the left one place value at a time. Write the sum of each column below the horizontal line, aligned by place value. For this example, the ones column sum is 9; the tens column sum is 7; the hundreds is 0; the thousands is 1. The sum of 1,045 and 34 is, therefore, 1,079.

Regrouping (Decomposing/Composing)

If the sum of any of the columns is more than 9, as in the following example, you need to regroup the digits.

\[\begin{align} 1\text{,}057& \\ \underline{+\quad 3\text{,}145}& \\ \end{align}\]

Add the first column: $7 + 5 = 12$, but $12$ is $10 + 2$ (or $1$ ten and $2$ ones), so write $2$ below the horizontal line at the ones column, and add $1$ on top of the tens column.

$\quad \quad \ \; \; 1$
$\begin{align} 1\text{,}057& \\ \underline{+\quad 3\text{,}145}& \\ 2& \\ \end{align}$

Then, proceed to add the tens column including the $1$ on top: $1 + 5 + 4 = 10$ (which is $1$ hundreds and $0$ tens), so we write $0$ at the tens column and $1$ on top of the hundreds column.

$\quad \quad\ \ \ \, 11$
$\begin{align} 1\text{,}057& \\ \underline{+\quad3\text{,}145}& \\ 02& \\ \end{align}$

Add the hundreds column ($1 + 0 + 1 = 2$), then the thousands column ($1 + 3 = 4$). The sum of $1\text{,}057$ and $3\text{,}145$ is $4\text{,}202$.

$\quad \quad \ \ \ \, 11$
$\begin{align} 1\text{,}057& \\ \underline{+\quad3\text{,}145}& \\ 4\text{,}202& \\ \end{align}$

Memorizing Addition Facts

For fluency in future math endeavors, you should memorize the basic math facts for adding single digit numbers. This means from 0 + 0 to 9 + 9. You should be able to think of the answer instantly without making notes or counting on your fingers. This is a simple task, but very important. Later, when you have to do longer and more involved calculations, you’ll avoid having to stop and get a calculator or write the problem down, either of which can cause you to lose your place in the current problem. Knowing the addition facts will also enable you to answer simple subtraction problems quickly.

Subtraction

Subtraction is the operation that finds the difference between two numbers. It is the opposite of addition. You can think of it as finding out how much larger one number is than another. In a word problem, some of the key words that tell you to subtract are difference, less or less than, more or more than, minus, or decrease.

Basic Subtraction in Columns

Subtraction, as with other arithmetic operations, is much easier to perform if done vertically. Start subtracting from the ones column, moving to the left or the bigger place values. In $76 – 25$, $76$ is the minuend while $25$ is the subtrahend. Write the minuend on top and the subtrahend below, carefully aligning the digits that correspond to the same place value.

\[\begin{align} 76& \\ \underline{-\quad 25}& \\ \end{align}\]

Write the difference of the digits in each column under the horizontal line. The difference for the ones column is $6 – 5 = 1$, and the difference for the tens column is $7 – 2 = 5$. The result of subtracting $25$ from $76$ is, therefore, $51$. This calculation can be verified by adding the resulting answer, $51$, with the portion subtracted, $25$, to arrive back at the original whole of $76$.

\[\begin{align} 76& \\ \underline{-\quad 25}& \\ 51& \\ \end{align}\]

Regrouping (Composing/Decomposing)

When any digit of the subtrahend is larger than the minuend, there is a need to perform regrouping, as in this example:

\[\begin{align} 2\text{,}061& \\ \underline{-\quad 543}& \\ \end{align}\]

Expand each number to show the value of each digit:

\[\begin{align} {2\text{,}000 + 0 + 60 + 1}& \\ \underline{-\quad 500 + 40 + 3}& \\ \end{align}\]

Since we cannot subtract a number from another number which is smaller within a column (such as, $3$ from $1$ and $500$ from $0$), we borrow one unit from the number on the left column. So we regroup the minuend by “borrowing” one unit from the tens column and adding that to the number in the ones column, and by borrowing one unit from the thousands column and adding that to the number in the hundreds column.

\[\begin{align} {1\text{,}000 + 1000 + 50 + 11}& \\ \underline{-\quad (500 + 40 + 3)}& \\ {1\text{,}000 + 500 + 10 + 8}& \\ \end{align}\] \[\text{Answer: } 1\text{,}518\]

Multiplication

Multiplication is repeated addition in that the numbers are being combined to reach a higher result, and it’s useful when you need to combine many identical numbers. For example, if you have eight pails, each one with nine potatoes, how many potatoes do you have? If you know that eight groups of nine is the same as $8 \times 9$ and $8 \times 9 = 72$, you won’t have to add all those nines together.

Some of the words that tell you to multiply in a word problem are times and product. Also, the word of means multiply in cases like “one-fifth of” or “thirty-five percent of.”

Modeling Multiplication

Using a figure we saw back in the area section, multiplication can be thought of as a rectangular collection of squares. We can look at the rectangle and see that there are 7 rows, each having 12 squares. The total number of squares, if you care to count them, is 84, which is also the product of 7 x 12. This helps to show why multiplication works the way it does.

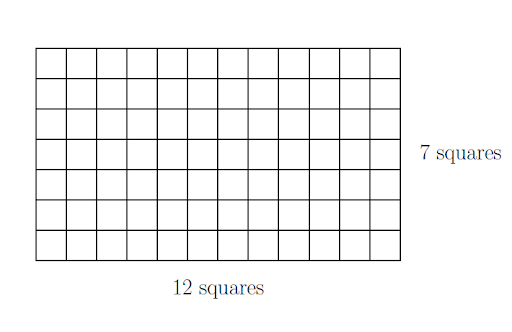
23 Modeling Multiplication.png

Simple Multiplication

You won’t have to do anything crazy on this test, like multiply two four-digit numbers, but you should be able to multiply a four-digit number by a one-digit number, or a two-digit number by another two-digit number.

Multiplication in Columns

To perform long-hand or manual multiplication, start off by writing the factors (or the numbers to be multiplied) vertically. The number written on top is the multiplicand, while the one below is called the multiplier. Align digits according to their place value, with ones on the right and increasing place values toward the left. To multiply $23$ by $56$, first write it as such:

\[\begin{align} 23& \\ \times \underline{\quad 56}& \\ \end{align}\]

We start by multiplying the ones digit ($6$) of the multiplier with every digit of the multiplicand. Write the result directly below the horizontal line, properly aligning the last digit under the ones column. At this point, don’t mind the commas:

\[\begin{align} 23& \\ \times \underline{\quad 56}& \\ 138& \\ \end{align}\]

We then proceed by multiplying the tens digit ($5$) of the multiplier with every digit of the multiplicand. Write the result below the previous result, aligning the last digit with the tens column. You can use a placeholder zero, as shown here, to remind you to align with the proper column each time.

\[\begin{align} 23& \\ \times \underline{\quad 56}& \\ 138& \\ 115\phantom{8}& \\ \end{align}\]

Vertically add the results of the multiplication to get the product of $23$ and $56$.

\[\begin{align} 23& \\ \times \underline{\quad 56}& \\ 138& \\ \underline{115\phantom{8}}& \\ 1288& \\ \end{align}\]

Memorizing Multiplication Facts

Like the memorization of addition facts, knowing the multiplication facts for numbers between $0 \times 0$ and $9 \times 9$ is a must! When you are calculating longer, involved problems, you won’t have time to stop and figure out these simple problems—the answers need to be in your head.

Division

Division is an operation that is the opposite of multiplication. The point of division is to find out how many of one number it will take to equal another number.

Some key words or phrases that tell us to divide are quotient, into, each, per, how many times, or goes into.

Models of Division

Looking back at the rectangle model we used to show that $7 \times 12 = 84$, we can think of that in a different way. How many rows of $12$ squares did it take to give us $84$ squares? Seven, right? In other words, we can say that $84$ divided by $12$ equals $7$.

Or we can ask how many columns of $7$ squares did it take to give us $84$ squares. That is, $84$ divided by $7$ equals $12$.

Simple Division

The most common division symbol is $\div$. Sometimes a fraction bar $/$ is used.

\[32 \div 8 = 4\] \[32/8 = 4 \text{ or } \frac{32}{8} = 4\]

“Long” Division

Division of some numbers may simply require a quick recall from memory, such as $100 \div 4 = 25$ or $36 \div 6 = 6$. This test, however, usually involves multi-step division, with or without a remainder or decimal in the result.

The larger number is called the dividend; the smaller number is the divisor. The divisor is written before the long division symbol, the dividend is written inside, and the result (the quotient) is written on top of the symbol.

Step 1: To calculate $8\text{,}528 \div 41$, write the numbers as:

\[\require{enclose} \begin{array}{r} 41 \enclose{longdiv}{8528} \\[-3pt] \end{array}\]

Step 2: Divide every digit of the dividend by the divisor and write the answer on top of the digit being divided. In this example, we can start by examining the dividend to see whether the first digit is large enough to be divided by the divisor – we find that it’s not ($8$ is smaller than $41$). So we take two digits ($85$) and divide $85$ by $41$ to get $2$. Write $2$ on top of the symbol and align it with $5$:

\[\require{enclose} \begin{array}{r} 2 \; \; \; \, \\[-3pt] 41 \enclose{longdiv}{8528} \\[-3pt] \end{array}\]

Step 3: Multiply $41$ by $2$ and write the product below $85$:

\[\require{enclose} \begin{array}{r} 2 \; \; \; \, \\[-3pt] 41 \enclose{longdiv}{8528} \\[-3pt] \underline{82}\phantom{2} \phantom{8} \\[-3pt] \end{array}\]

Step 4: Subtract $82$ from $85$ to get $3$. Bring down $2$ from the dividend:

\[\require{enclose} \begin{array}{r} 2 \; \; \; \, \\[-3pt] 41 \enclose{longdiv}{8528} \\[-3pt] \underline{82}\phantom{2} \phantom{8} \\[-3pt] 32 \phantom{8} \\[-3pt] \end{array}\]

Step 5: Divide $32$ by $41$ to get $0$. Repeat step $3$ and step $4$:

\[\require{enclose} \begin{array}{r} 20 \; \; \\[-3pt] 41 \enclose{longdiv}{8528} \\[-3pt] \underline{82}\phantom{2} \phantom{8} \\[-3pt] 32 \phantom{8} \\[-3pt] \underline{0} \phantom{3} \\[-3pt] \quad \; 328 \\[-3pt] \end{array}\]

Step 6: Divide $328$ by $41$ to get $8$. Repeat step $3$ and step $4$:

The answer is $208$. The procedure is simply repeated until the last digit.

Remainders

Remainders (when the result of subtraction in the last step is not $0$) can be presented in three ways:

as $r.$ followed by the remainder
as a fraction with the remainder as the numerator, and the divisor as the denominator
as digits after a decimal point when division is continued after the whole number part of the quotient (this involves adding zeros after the last digit of the dividend)

You may be asked to do a division problem that results in a quotient with a remainder. For example, in the division below, we see a quotient of $14$ with a remainder of $2$.

\[\require{enclose} \begin {array}{r} 14 \\[-3pt] 3 \enclose{longdiv}{44} \\[-3pt] \underline{3}\phantom{4} \\[-3pt] 14 \\[-3pt] \underline{12}\\ 2 \\[-3pt] \end{array}\]

We can write this result by using a capital $R$, $\ 14\ R2$, or take the remainder and write it over the divisor, $14 \frac{2}{3}$.

Inverse Operations

Addition and subtraction are opposite or “inverse” operations. One of them undoes what the other one does. For example, in the first calculation below, $6$ is subtracted from $18$ to get a result of $12$. The second calculation adds $6$ to the $12$, getting $18$ back again, and reversing what was done to the $18$.

$18 - 6 = 12$
$12 + 6 = 18$

This idea comes in handy when you want to check your answer to an addition or subtraction problem. Suppose you have done this subtraction: $37 - 14 = 23$. You then check your answer by adding $14$ to the $23$ and see if you get $37$ as an answer. If you do, then you’ve done the problem right.

In a similar way, multiplication and division are inverse operations. If you divide $35$ by $5$ and get $7$, you can then check your answer by multiplying $7$ by $5$ to see if you get $35$ back.

$35 \div 5 = 7$
$7 \times 5 = 35$

Operations with Decimals

Except for locating the decimal point, the basic operations work the same way for decimals as for whole numbers. You should be able to add, subtract, multiply, and divide decimals out to the hundredths place, as shown below.

If you struggle with decimal understanding, it may be helpful to use drawings or models to visualize decimal meaning. For example, the number $1.24$ can be illustrated like this:

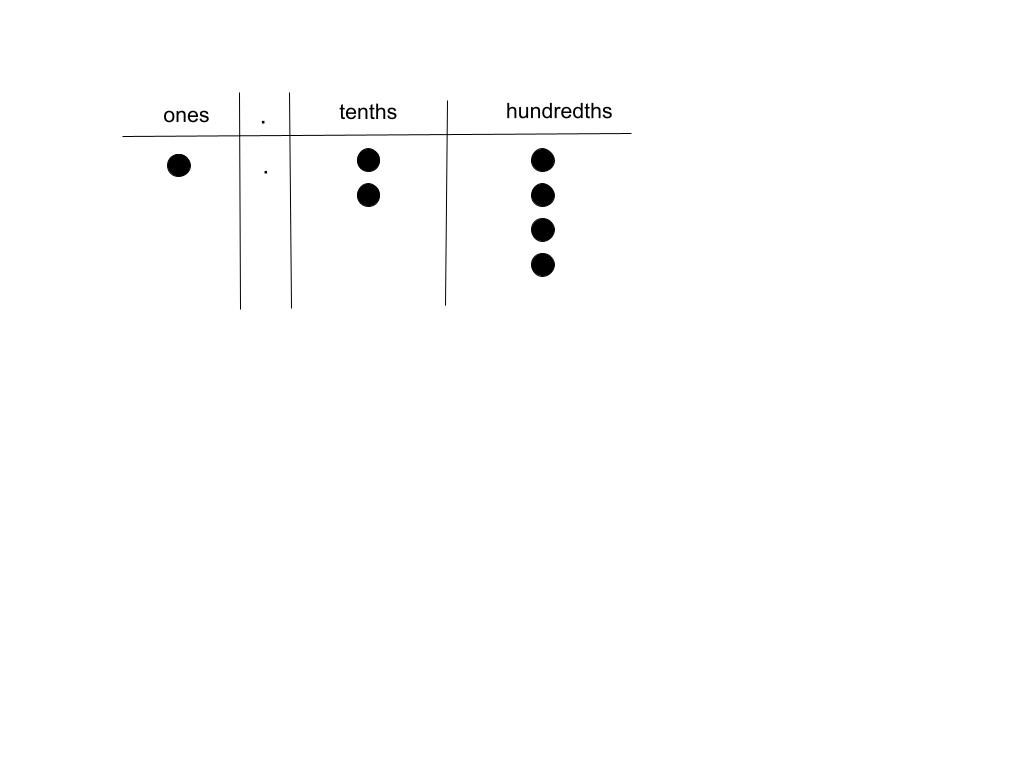
24 Visual for Decimal Number.jpg

Then, if you have to perform addition or subtraction, you can visually do that, also.

Also, be sure you can explain the “why” of decimal operations. This also helps you to be sure you have obtained the correct answer. For example:

“$4.25 \cdot 3.5$ will have three decimal places in the answer because there are a total of three decimal places in the numbers being multiplied.”

Adding and Subtracting Decimals

The numbers to be added or subtracted are written vertically: digits are aligned according to their place value, just like when you add non-decimal numbers. All decimal points are aligned, as well.

Addition follows in much the same manner as the addition of whole numbers shown earlier, except for the decimal point which separates the whole and decimal numbers. Regrouping will be necessary if a column’s sum is over $9$, just like in regular addition.

Subtraction of decimal numbers is similar to subtraction of whole numbers too. Regrouping will also be necessary when a digit is larger than the digit it must be subtracted from.

Multiplying Decimals

Multiplying decimal numbers starts in the same way we multiply whole numbers, and differs only in the last few steps. Simply multiply the numbers, ignoring the decimals for now.

If you multiply $7.65$ by $9.8$, you would work as if you were multiplying $765$ by $98$. The answer to that would be $74\text{,}970$.

Count the total number of decimal places in both the multiplier and the multiplicand: $1 + 2$ decimal places. Move the decimal three places from the right toward the left, and get the final answer of $74.970$. The last zero(s) after the decimal can be dropped and the number will retain its value, giving you $74.97$

Dividing Decimals

Division of decimals is similar to division of whole numbers, except for the presence of the decimal point and a few added steps.

First, move the decimal point in the divisor to the right until it becomes a whole number.
Move the decimal point in the dividend to the right the same number of places that you moved the decimal in the divisor.
Now, put a decimal point in the quotient area, directly above its spot in the dividend. That is where it will be in the answer.

Note: You may add zero and proceed with the division up to the required number of decimal places.

Mental Math

Be able to mentally add or subtract 10 from any two digit number. Luckily, it’s not hard. Just add or subtract 1 from the tens place.

For example, what is 10 more than 58? Just add 1 to the 5 and write 68.
What is 10 less than 32? Just subtract 1 from the 3 and write 22.

It works because by adding or subtracting 1 in the tens place, you are actually adding or subtracting ten to or from the original number.

Sometimes, you just don’t need all the digits given. The population of Michigan in 2021 was 9,992,427. If we think of it at all, we probably ignore most of those digits and think 10 million.

Rounding Numbers

In some cases, we just want a quick approximate answer to a problem. For example, suppose you pick up three items in the grocery store for $4.98, $3.10, and $2.95. You could do some quick rounding and adding to get an estimate of your bill to make sure you have enough money. Your thinking would go something like this: Round the numbers to the nearest dollar (5, 3, 3) and add them. You have 5 + 3 + 3 = $11.

Rounding Whole Numbers

Using knowledge of place value, whole numbers can be rounded to any place value you want, assuming that place exists in the number. The basic idea is this: Look at the digit in the place you need to round to. If there is a 5 or greater to the right of that digit, add 1 to the digit. Change all digits to the right to zeros.

Examples:

Round 136 to the nearest ten.

The digit 3 is in the tens place. Look to its right and you see the 6. That’s greater than 5, so add 1 to the three and write zero in place of the 6, giving you 140. This is called rounding up (136 was rounded up to 140).

Round 672 to the nearest ten.

The digit 7 is in the tens place. Look to its right and you see the 2. That’s less than 5 so you don’t add 1 to the 7, but you still write a zero in place of the 2, giving you 670. This is rounding down (672 was rounded down to 670).

Round 5,470 to the nearest thousand.

The digit 5 is in the thousands place. Look to its right and see the 4. That’s less than 5, so you don’t add 1 to the 5, and you write zeros in place of the 4 and 7. This is also rounding down (5,470 was rounded down to 5,000).

Rounding Decimals

Rounding decimals is exactly like rounding with whole numbers, except after rounding, you don’t add any zeros to the right. Instead, you drop those digits.

Examples:

Round 9.268 to the nearest hundredth.

The digit 6 is in the hundredth place. Look to its right and see the 8. That’s more than 5, so you add one to the 6, and drop the 8, giving you 9.27.

Round 0.3642 to the nearest tenth.

The digit 3 is in the tenths place. Look to its right and see the 6. That’s more than 5, so add 1 to the 3 and drop the 642, giving you 0.4. (Don’t worry about the zero to the left of the decimal point. That’s just there to help keep us from missing the decimal point. It doesn’t affect rounding.)