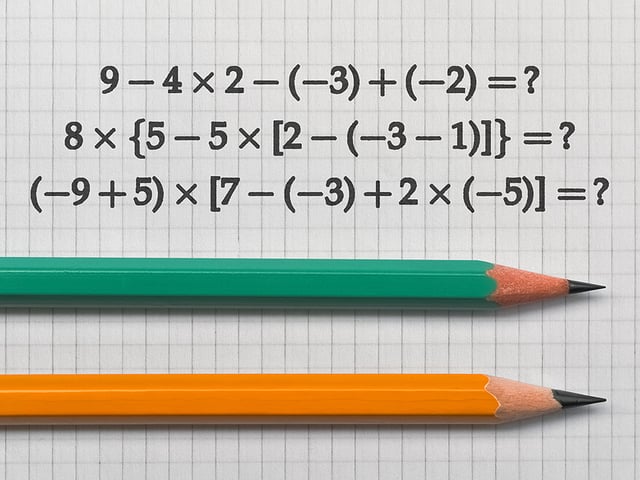
Formula Chart for Numbers and Operations on the SBAC Test

Most people say that Math is hard for them. Does this sound like you? Are you wondering how to ace the SBAC Test? Well,

Math is like music: a set of rules that, when applied correctly, create beauty.

Do you want to succeed on the SBAC Test? You’ll need to know the rules. In the following chart, you’ll find the essential rules you’ll need to apply when solving Numbers and Operations Questions on the SBAC Test. Use the rules and create your own “math music.”

Also, be sure and utilize our four other formula charts as you prepare for this test:

Algebra

Functions

Geometry

Statistics and Probability

Numbers and Operations Formulas for the SBAC

Category	Formula	Symbols	Comment
Properties of Rational Numbers	\(a+b=b+a\) \(a \cdot b = b \cdot a\)	a, b = any constant or variable	Commutative Property
Properties of Rational Numbers	\(a+(b+c)=(a+b)+c\) \(a \cdot (b \cdot c)=(a \cdot b) \cdot c\)	a, b, c = any constant or variable	Associative Property
Properties of Rational Numbers	\(a \cdot (b+c)=a \cdot b + a \cdot c\)	a, b, c = any constant or variable	Distributive Property
Properties of Rational Numbers	\(a+0=a\)	a = any constant or variable	Identity Property of Addition
Properties of Rational Numbers	\(a \cdot 1 = a\)	a = any constant or variable	Identity Property of Multiplication
Properties of Rational Numbers	\(\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{(a \cdot d)+(c \cdot b)}{(b \cdot d)}\)	a, b, c, d = any real number	Remember to simplify the fraction if possible.
Properties of Rational Numbers	\(\dfrac{a}{b} \cdot \dfrac{c}{d}=\dfrac{a \cdot c)}{(b \cdot d)}\)	a, b, c, d = any real number	Remember to simplify the fraction if possible.
Properties of Rational Numbers	\(\dfrac{a}{b} \div \dfrac{c}{d}=\dfrac{a \cdot d)}{(b \cdot c)}\)	a, b, c, d = any real number	Remember to simplify the fraction if possible.
Properties of Rational Numbers	\(a\dfrac{b}{c}=\dfrac{(a \cdot c)+b}{c}\)	a, b, c = any real number	Remember to simplify the fraction if possible.
Properties of Exponents	\(x^a \cdot x^b = x^{a+b}\)	a, b, x = any real number	Remember to simplify the fraction if possible.
Properties of Exponents	\(\frac{x^a}{x^b}=x^{a-b}\)	a, b, x = any real number
Properties of Exponents	\((x^a)^b = x^{a \cdot b}\)	a, b, x = any real number
Properties of Exponents	\((x \cdot y)^a = x^a \cdot y^a\)	a, x, y = any real number
Properties of Exponents	\(x^1 = x\)	x = any real number
Properties of Exponents	\(P=(2 \cdot l)+(2 \cdot w)\)	x = any real number
Properties of Exponents	\(x^{-a} = \frac {1}{x^a}\)	a, x = any real number
Percentages	\(a \cdot b\%=a \cdot \dfrac{b}{100}\)	a = any real number b% = any percent	Remember to simplify if possible.
Percentages	\(\% = \dfrac{\vert b-a \vert}{b} \cdot 100= \dfrac{c}{b} \cdot 100\)	% = % increase or decrease a = new value b = original value c = amount of change
Units	\(Du=Su \cdot \dfrac{Du}{Su}=Su \cdot CF\)	Du = Desired Unit Su = Starting Unit CF = Conversion Factor	Multiple steps may be needed