Formula Chart for Functions on the SBAC Test

Functions are like tiny math machines: You feed them numbers and they give you another number as an output. Fantastic…right? Maybe you’re not as excited as we are, but acing functions questions on the SBAC test will require you to become an expert on working with these machines. And probably the best way to achieve that is getting to know them in advance. The following chart contains the most important functions you need to know for the SBAC Test. You won’t be able to use it during the test, but it will help you learn how to manipulate them before it.

Also, be sure to access our other four formula charts for the SBAC Math Test:

Algebra

Geometry

Number and Operations

Statistics and Probability

Feel free to also check out the FREE sample SBAC Test problems we have for you here at Union Test Prep!

Formulas for Functions on the SBAC

Name	Graph	Equation	Domain	Range
Constant		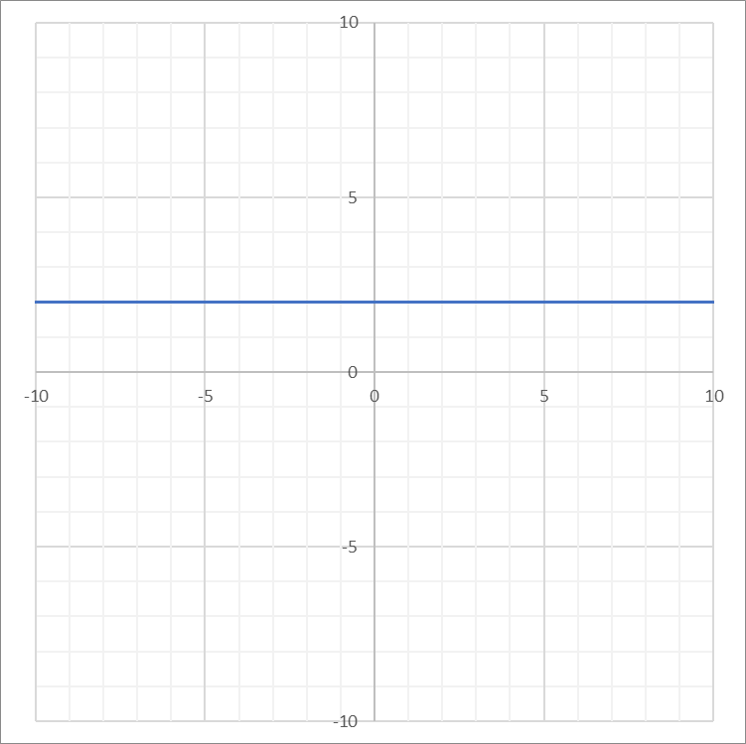\(f(x)=c\)	\((-\infty, \infty)\)	\(\{y:y=c\}\)
Identity or Linear		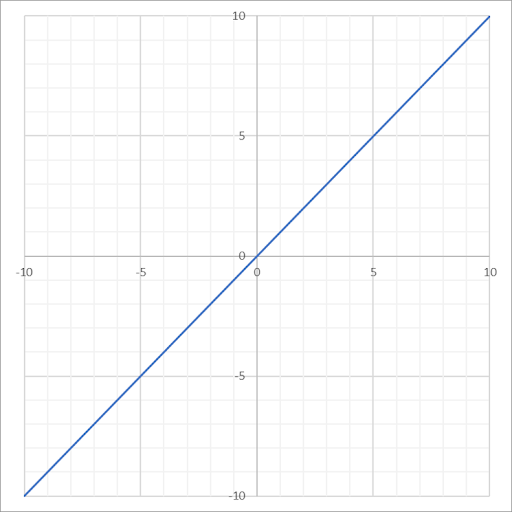\(f(x)=x\)	\((-\infty, \infty)\)	\((-\infty, \infty)\)
Absolute Value		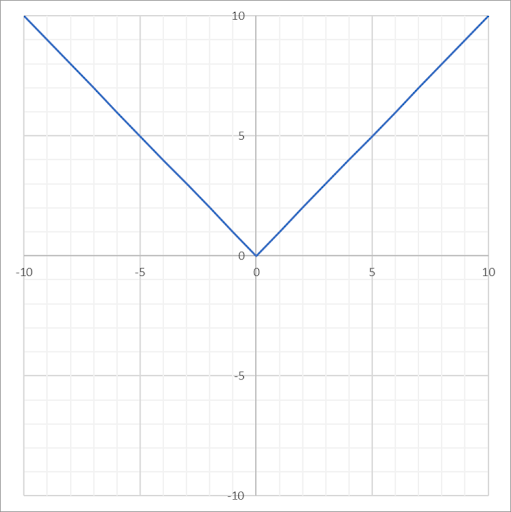\(f(x) = \vert x \vert\)	\((-\infty, \infty)\)	\([0, \infty)\)
Greatest Integer		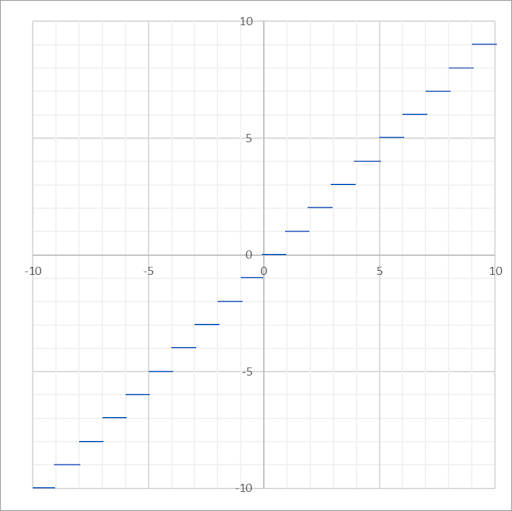\(f(x) = int(x)=[x]=floor(x)\)	\((-\infty, \infty)\)	\(\{ y:y \in Z \}\)
Quadratic or Square		\(f(x) = x^2\)	\((-\infty, \infty)\)	\([0, \infty)\)
Square Root		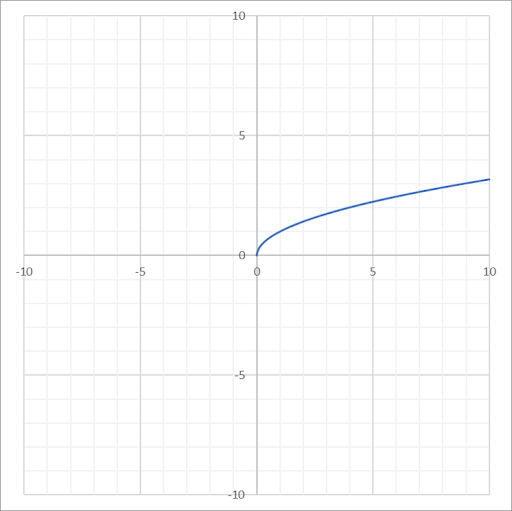\(f(x) = \sqrt{x}\)	\([0, \infty)\)	\([0, \infty)\)
Cubic		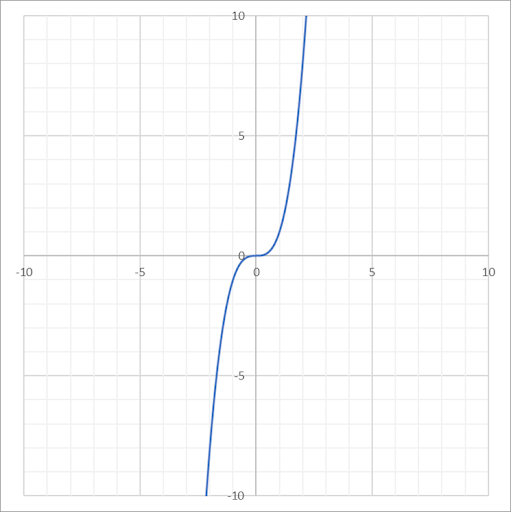\(f(x) = x^3\)	\((-\infty, \infty)\)	\((-\infty, \infty)\)
Cubic Root		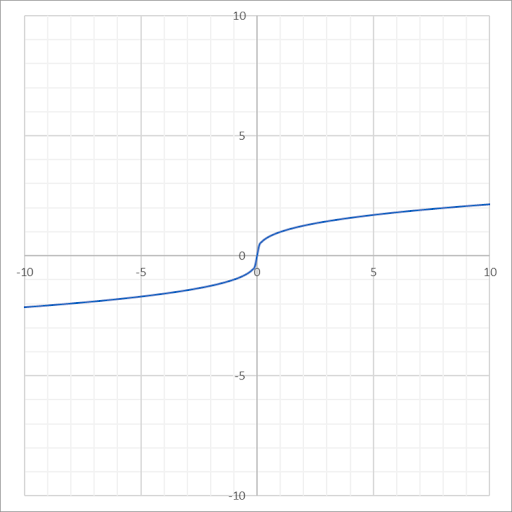\(f(x) = \sqrt[3]{x}\)	\((-\infty, \infty)\)	\((-\infty, \infty)\)
Exponential		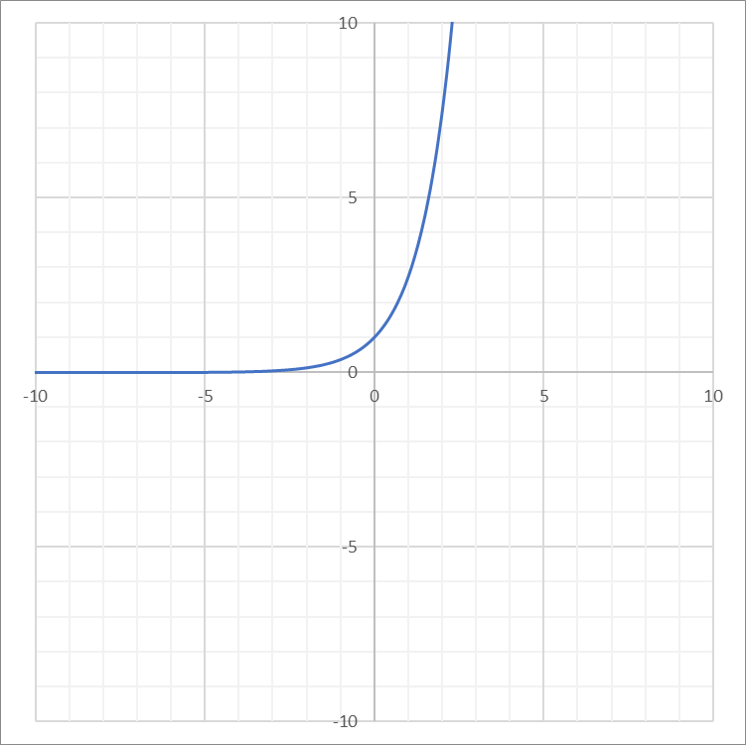\(f(x) = 10^x\) or \(f(x) = e^x\)	\((-\infty, \infty)\)	\((0, \infty)\)
Logarithmic		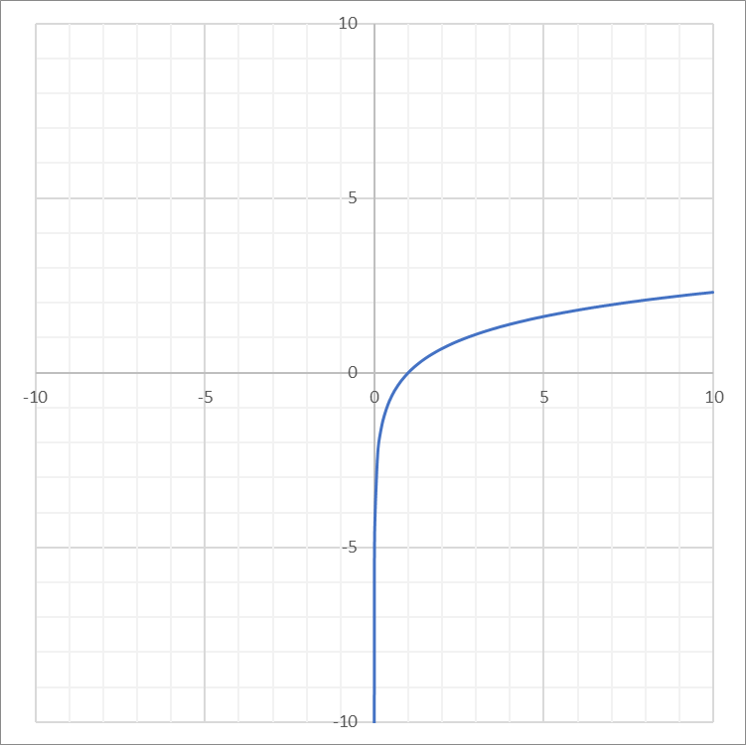\(f(x) = log(x)\) or \(f(x) = ln(x)\)	\((0, \infty)\)	\((-\infty, \infty)\)
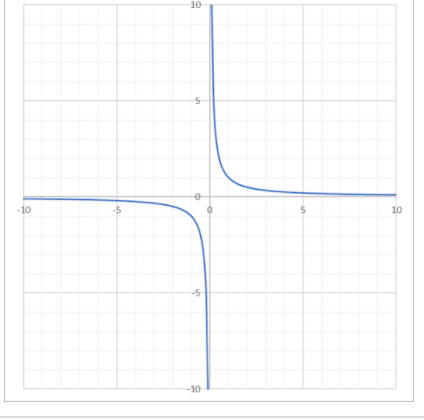
Rational or Reciprocal		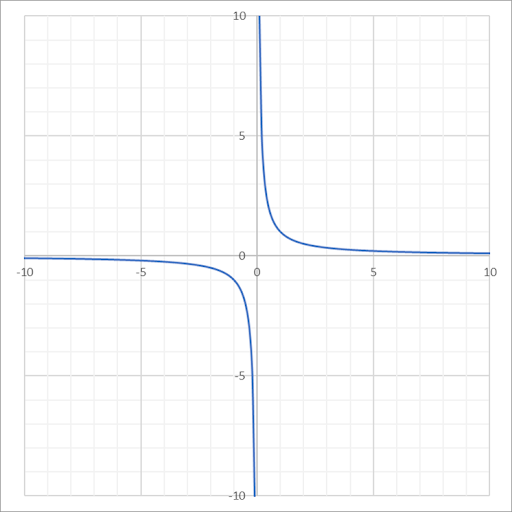\(f(x) = \dfrac{1}{x}\)	\((-\infty,0) \cup (0, \infty)\)	\((-\infty,0) \cup (0, \infty)\)
Sine		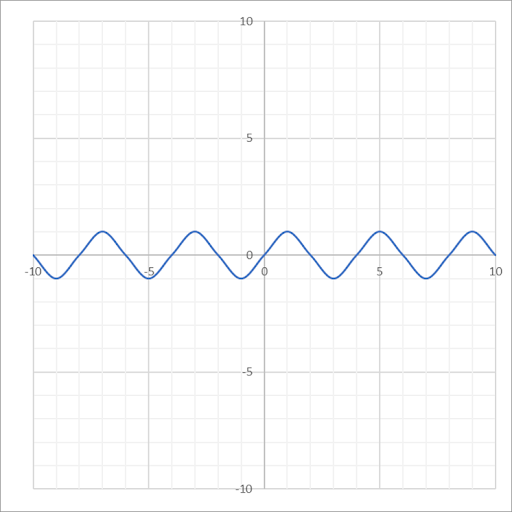\(f(x) = A \cdot sin(Bx-C) +D\) where \(A\) = Amplitude \(\dfrac{2 \pi}{B}\) = Period \(\dfrac{C}{B}\) = Phase Shift \(D\) = Vertical Shift	\((-\infty, \infty)\)	\([-1+D, 1+D]\)
Cosine		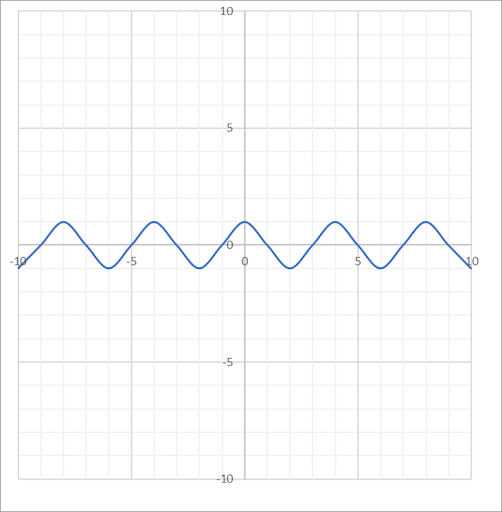\(f(x) = A \cdot cos(Bx-C) +D\) where \(A\) = Amplitude \(\dfrac{2 \pi}{B}\) = Period \(\dfrac{C}{B}\) = Phase Shift \(D\) = Vertical Shift	\((-\infty, \infty)\)	\([-1+D, 1+D]\)
Tangent		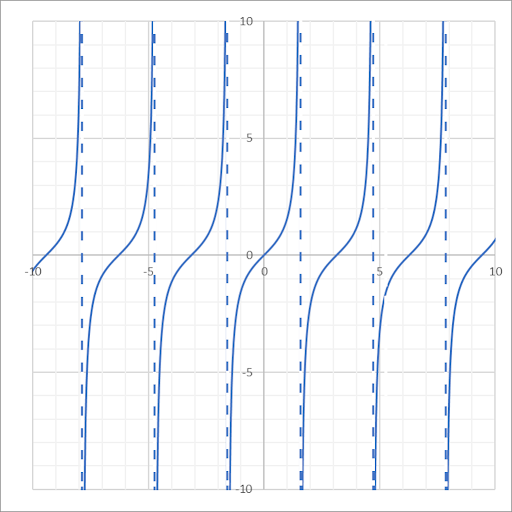\(f(x) = tan(x) = \dfrac{sin (x)}{cos(x)}\)	\((-\infty, \infty)\) except \(x=\frac{\pi}{2} \pm n\pi\)	\((-\infty, \infty)\)