
Formula Chart for Geometry on the SBAC Test
Geometry is literally everywhere! It’s in the shape of the stars and planets, in the food you eat, in your smartphone, and even in the icons for the apps in your smartphone. All the different shapes in the universe can be described by formulas and equations, and for Geometry on the SBAC Test, you need to know how to handle those formulas. The following chart is intended for study purposes only, as you won’t be able to use it during the actual test, but is really helpful to learn how to handle them when solving Geometry problems on the SBAC Test!
You can find free practice for the SBAC at Union Test Prep.
And you can find our other four formula charts for this test here:
Geometry Formulas for the SBAC
| Category | Formula | Symbols | Comment |
|---|---|---|---|
| Transformations | \((x,y)\rightarrow(x, -y)\) | Reflection x-axis | |
| Transformations | \((x,y)\rightarrow(-x, y)\) | Reflection y-axis | |
| Transformations | \((x,y)\rightarrow(-x, -y)\) | Reflection Origin | |
| Transformations | \((x,y)\rightarrow(y, x)\) | Reflection line y = x | |
| Transformations | \((x,y)\rightarrow(-y, -x)\) | Reflection line y = -x | |
| Transformations | \((x,y)\rightarrow(y, -x)\) | Rotation \(90^o\) Counterclockwise | |
| Transformations | \((x,y)\rightarrow(-x, -y)\) | Rotation \(180^o\) Counterclockwise | |
| Transformations | \((x,y)\rightarrow(x+a, y+b)\) | Translation | |
| Transformations | \((x,y)\rightarrow(rx, ry)\) | Dilation (r = scale factor) | |
| Right Triangles | \(a^2+b^2=c^2\) | a, b = legs of a right triangle c = hypotenuse of a right triangle |
Pythagorean Theorem |
| Coordinates | \(y = m \cdot x + b\) | y = dependent variable m = slope x = independent variable b = y-axis intercept |
Slope-Intercept Form of a line: Try to convert any given linear equation to this form. |
| Coordinates | \(m= \frac{(y_2-y_1)}{(x_2-x_1)}\) | \(m\) = slope \(y_n\) = dependent variable at point n \(x_n\) = independent variable at point n |
This is a rearranged version of the point-slope form. |
| Coordinates | \(y-y_1=m(x-x_1)\) | \((x_1, y_1)\) = point on the line y = dependent variable x = independent variable m = slope |
Point-slope form of a line |
| Coordinates | \(d=\sqrt{(y_2-y_1)^2 +(x_2-x_1)^2}\) | d = distance between two points \(y_n\) = y value at point n \(x_n\) = x value at point n |
|
| Coordinates | \((x_m, y_m) = (\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2})\) | \(x_m\) = x value at the midpoint \(y_m\) = y value at the midpoint \(y_n\) = y value at point n \(x_n\) = x value at point n |
|
| Volume | \(V=l \cdot w \cdot h\) | V = volume of rectangular prism l = length w = width h = height |
|
| Volume | \(V = \frac{1}{3} \cdot l \cdot w \cdot h\) | V = volume of pyramid l = length w = width h = height |
|
| Volume | \(V = \pi \cdot r^2 \cdot h\) | V = volume of a cylinder r = radius h = height |
|
| Volume | \(V= \frac{4}{3} \cdot \pi \cdot r^3\) | V = volume of a sphere r = radius |
|
| Circles | \(C = 2 \cdot \pi \cdot r\) \(C = \pi \cdot d\) |
C = circumference (perimeter) r = radius d = diameter \(\pi\) = 3.14 |
|
| Circles | \(s = r \cdot \theta\) | s = arc length r = radius \(\theta\) = central angle (radians |
|
| Circles | \(A = \pi \cdot r^2\) | A = area of a circle r = radius |
|
| Conic Sections | \((x-h)^2 + (y-k)^2 = r^2\) | \((h, k)\) = center of circle r = radius |
Standard form of a circle |
| Conic Sections | \((x-h)^2 = 4p \cdot (y-k)\) | \((h, k)\) = vertex of a parabola p = distance from vertex to directrix |
Parabola that opens up or down |
| Conic Sections | \((y-k)^2 = 4p \cdot (x-h)\) | \((h, k)\) = vertex of a parabola p = distance from vertex to directrix |
Parabola that opens left or right |
| Shapes | \(A=\frac{1}{2} \cdot b \cdot h\) | A = area of a triangle b = base h = height |
|
| Shapes | \(A = s^2\) | A = area of a square s = side length |
|
| Shapes | \(A=l \cdot w\) | A = area of a rectangle l = length w = width |
|
| Shapes | \(A=h \cdot \frac{(b_1+b_2)}{2}\) | A = area of a trapezoid \(b_n\) = base n h = height |
Trigonometry
Keep Reading
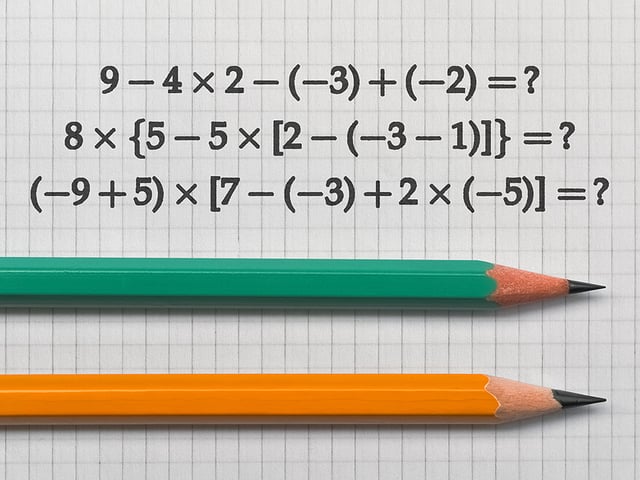
Smarter Balanced Assessment Consortium Blog
Formula Chart for Numbers and Operations on the SBAC Test
Most people say that Math is hard for them. Does this sound like you? A…

Smarter Balanced Assessment Consortium Blog
Formula Chart for Algebra on the SBAC Test
Have you ever painted by number? It’s probably the easiest way to paint…
Smarter Balanced Assessment Consortium Blog
Formula Chart for Functions on the SBAC Test
Functions are like tiny math machines: You feed them numbers and they g…