Mathematics Study Guide for the ParaPro Assessment

Geometry and Measurement

Geometry is the study of shapes. This test will require some knowledge of geometry as well as measurements and their units.

Time

You’ve been reading clocks to determine the time your whole life, so we won’t insult your intelligence. You should already know that $30$ minutes is $\frac{1}{2}$ hour and $15$ minutes is $\frac{1}{4}$ (quarter) hour. The tricky thing to look out for in a test like this will be the usage of “past/after” vs. “til/before”.

Ex: What time is “quarter after $5$”? ($5\text{:}00 + 0\text{:}15 = 5\text{:}15$)

Ex: What time is “$5$ minutes til $7$”? ($7\text{:}00 - 0\text{:}05 = 6\text{:}55$)

Remember: There are $60$ seconds in a minute and $60$ minutes in an hour.

Money

It’s important to remember:

$100$¢ = $\$1$
Pennies are $1$¢ = $\$0.01$
Nickels are $5$¢ = $\$0.05$
Dimes are $10$¢ = $\$0.10$
Quarters are $25$¢ = $\$0.25$

Example:

How much money is $3$ dollars, $2$ quarters, $1$ dime, $3$ nickels, and $4$ pennies?

Solution:

$3$ dollars = $\$3.00$
two quarters are $2 \cdot \$0.25 = \$0.50$
$1$ dime = $\$0.10$
$3$ nickels are $3 \cdot \$0.05 = \$0.15$
$4$ pennies are $4 \cdot \$0.01 = \$0.04$

So:

\[\begin{align} $3.00& \\ $0.50& \\ $0.10& \\ $0.15& \\ \underline{+\quad $0.04 }& \\ $3.79& \\ \end{align}\]

Unit Conversion

In order to correctly convert units, it’s important to know basic prefixes for the metric system.

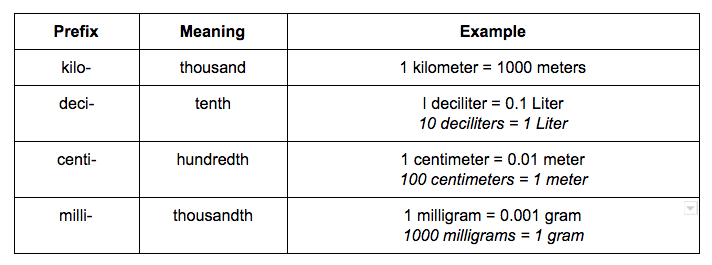
Also, remember the basics of the standard American system.

Distance

$1$ mile = $5280$ feet
$1$ yard = $3$ feet
$1$ foot = $12$ inches

Liquid Volume

$1$ gallon = $4$ quarts = $8$ pints = $16$ cups = $128$ fluid ounces

Weight

$1$ pound = $16$ ounces
$1$ ton = $2000$ pounds

Finally, know how to go between the two. Here are some common conversions:

Distance

$1$ inch = $2.54$ centimeters
$1$ mile = $1.61$ km

Liquid Volume

$1$ gallon = $3.8$ liters
$1$ liter = $4.2$ cups

Weight

$1$ kilogram = $2.2$ pounds

How to Convert

To perform any conversion, create a proportion (two ratios set equal to each other) and solve.

Example:

Convert $8$ cups into liters.

Solution:
We’ll create a proportion $\frac{cups}{liters}= \frac{cups}{liters}$ using the conversion we know: $4.2$ cups = $1$ liter.

It’s also important to define a variable, say $x$, for the unknown quantity of liters.

Proportion: $\frac{8 \;cups}{x\; liters} = \frac{4.2 \;cups}{1 \;liter}$: $\frac{8}{x} = \frac{4.2}{1}$

A way to solve this proportion is to cross multiply and isolate:

\[8 = 4.2x\]

Divide both sides by $4.2$ and you’ll get roughly $1.9 = x$
So, $8$ cups is around $1.9$ liters.

Another example:

How many pounds is $5$ kilograms?

Solution:

Use this proportion: $\frac{pounds}{kg}=\frac{pounds}{kg}$

Keep in mind we know $2.2$ pounds = $1$ kg.

Proportion: $\frac{x \;pounds}{5 \;kg} = \frac{2.2 pounds}{1 \;kg}$ or $\frac{x}{5} = \frac{2.2}{1}$

Using cross multiplication, you should get $x = 11$.
So $5$ kilograms is $11$ pounds.

Basic Shapes

It’ll be important on this test to be familiar with names of basic shapes and terminology about them. First, a few definitions:

Polygon

A polygon is a flat closed figure bounded by straight segments called sides.

Sides intersect at points called vertices (singular: vertex).
The word polygon comes from poly (many) and gon (angles).
In a polygon, the number of sides is the same as the number of vertices.

Here’s a list of common polygons.

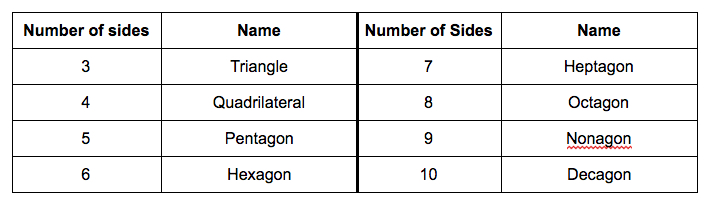
A polygon is regular if all its sides and angles are congruent. A square is a regular quadrilateral, for example.

Triangles

Triangles are the simplest of all polygons. Every polygon can be broken up into triangles. This is why we’ve developed an entire field of mathematics based just on the three-sided polygon: trigonometry. You’ll need to be familiar with the terminology to describe triangles.

All angles of any triangle add up to $180$ degrees.

Right triangles are used often in trigonometry, so there is a bit more terminology associated with them. Reference this image:

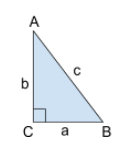
The side opposite the right angle ($c$) is called the hypotenuse. The other two sides ($a$ and $b$) are called legs.

An important theorem to remember is the Pythagorean theorem: In a right triangle, with legs $a$ and $b$, and hypotenuse $c$, $a^2+b^2=c^2$.

Circle

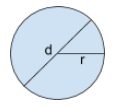
A circle is defined as the set of all points equidistant (the same distance) from a point called the center. The distance from one edge to another edge through the center is called the diameter. The distance from the center to the edge is called the radius. The length of the diameter is equal to twice the length of the radius. The circumference of a circle is its perimeter (the distance around).

3-D Shapes

A polyhedron is a $3$-dimensional closed figure bounded by polygons called faces. Two faces meet at line segments called edges. Three or more faces meet at points called vertices. There are two major types of polyhedron: pyramids and prisms. A pyramid has one face called the base and each side is a triangle sharing a common point. A prism has two congruent (parallel) bases and sides are formed by rectangles. You name pyramids and prisms for the shape of their base. Here are some examples:

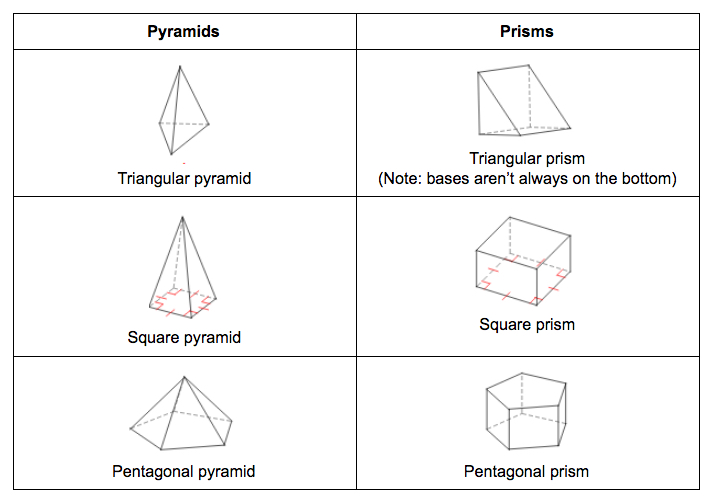
Note: Technically circles aren’t polygons (no straight edges), but one can think of cones as circular pyramids and cylinders as circular prisms. In a cone, the slant height is the distance from the edge of the circular base to the vertex (top).

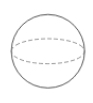
Speaking of circles, there is one more 3-dimensional figure: the sphere. A sphere has a similar definition to the circle: the set of all points (in 3-dimensions) equidistant from a point called the center. Spheres also have a radius and a diameter.

Measuring Shapes

There are two main measurements you’ll need to be able to find concerning $2$-dimensional shapes: perimeter (distance around an object) and area ($2$-dimensional space within the object). The variables used are:

s = side
l = length
w = width
h = height
b = base
r = radius
d = diameter

For three-dimensional objects, you’ll need to know how to find surface area and volume. The surface area of a polyhedron is just the sum of areas of all the faces. The volume is the amount of space enclosed within the polyhedron. For these formulas, this is what the letters mean:

B = area of the base
h = height
r = radius
C = circumference of the base
l = slant height

Graphing on the Coordinate Plane

The story goes that in the early 1600s, a French mathematician and philosopher Rene Descartes was watching a fly on his ceiling. He wanted to devise a plan to tell its location using only two values. If you’ve ever played the game Battleship, you know what he was going after. He invented the Cartesian coordinate plane: a flat space with two number lines intersecting perpendicularly at $0$. The point of intersection is called the origin. The two number lines are called the $x$-axis (horizontal) and the $y$-axis (vertical).

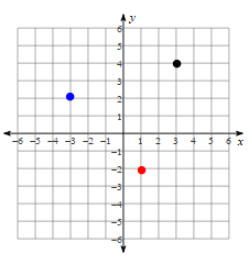
To locate a point on the coordinate plane, first name how far left or right it is from the origin ($x$-coordinate), followed by how far up or down it is from the origin ($y$-coordinate). In this case, the black dot is $3$ to the right and $4$ up. This location can be given as the ordered pair $(3, 4)$. The red dot would be at $(1, -2)$ and the blue dot is at $(-3, 2)$.