Mathematics Study Guide for the ParaPro Assessment

Percentages

The word “percent” can be broken into two parts: per- meaning “divided by”, and cent meaning “100”. (A century is $100$ years and there are $100$ cents in a dollar). So, $35\%$ means $35$ divided by $100$, or $35 \div 100 = \frac{35}{100}$.

Use the above knowledge to change percents into fractions.

To change a percent to a decimal, simply move the decimal point two places to the left (equivalent to dividing by $100$). So, $45\%$ would become $0.45$[.]

To go from decimal form to percent, do the reverse: $1.24 = 124\%$.

If you want to know how to change a fraction to a percent, see if you can write it as an equivalent fraction with $100$ as the denominator.

Example:

$\frac{3}{4} = \frac{75}{100}$, so $\frac{3}{4}$ is $75\%$.

Note: You can also change the fraction to a decimal and then to a percent.

Now, let’s look at the “common sense” problem proposed at the beginning:

“What is $25\%$ of $\$100$?”

Let’s change $25\%$ into a decimal ($0.25$) or a fraction ($\frac{25}{100} = \frac{1}{4}$).
The word of means “multiply” in word problems. So, we have $0.25 \cdot 100$ or $\frac{1}{4} \cdot 100$.
In both cases, the answer is $\$25$. The discount ($\$100 - $25$) would bring the price down to $\$75$.

Exponents

Exponents are numbers that indicate how many times to perform the multiplication of a number by itself.

Here is a list of properties of exponents:

$a^m \cdot a^n = a^{m+n}$
Example: $2^3 \cdot 2^5 = 2^{3+5}= 2^8$

$a^m \div a^n = a^{m-n}$
Example: $5^3 \div 5^2 = 5^{3-2}=5^1= 5$

$(a \cdot b)^m = a^m \cdot b^m$
Example: $(2x)^3 =2^3 \cdot x^3 = 8x^3$

$x^0 = 1$
Example: $123,871^0 = 1$

$a^{-n} = \frac{1}{a^n}$
Example: $2^{-3} = \frac{1}{2^3} = \frac{1}{8}$

Number Sequences

You’ll often be asked to find missing numbers in sequences or to find the pattern and predict the next number. For these problems, just try the operations (addition, subtraction, multiplication, division, and exponents) to determine the pattern.

Example: “Find the missing number in the sequence $1, -2, -5,$ ___, $-11$.”

You’ll notice that to move from the first to the second term, you can subtract $3$.
Do this again and you’ll get $-5$.
One more time and you’ll get $-8$, the answer.
Note: do it again and you’ll get $-11$, confirming you made the right choice.

Example: “Find the next term in the sequence $8, 4, 2, 1,$ ___.”

If you try subtraction, you’ll see $8-4$ is $4$, but $4-4$ is $0$, so it can’t be subtraction.

Maybe division works:
$8 \div 2 = 4, 4 \div 2 = 2, 2 \div 2 = 1$ so $1 \div 2$ gives $\frac{1}{2}$ as the answer.

Mental Math

Mental math is the best way to speed up your test-taking. Use estimation to allow problems to be done mentally. You can quickly check your answer to see if it’s reasonable, or you can eliminate wrong answers ahead of time.

Example: “What is $3.05 \cdot 4.9$?”

Answer choices:

$16.5$
$12.345$
$14.945$
$11.05$

First, estimate that $3.05 \cdot 4.9$ would be pretty close to $3 \cdot 5 = 15$. The answer would be $14.945$, the third answer choice. This is much faster than long multiplication.

Rounding

When rounding a number, remember this: If the next digit is $5$ or higher, round up.

Example: “Round $123.456$ to the nearest hundredth.”

The hundredth digit is $5$, so look at the next one: $6$.
$6$ is $5$ or higher, so round the hundredth digit up: $5$ to $6$.
Thus, $123.456$ rounds to $123.46$[.]

“Round the same number ($123.456$) to the nearest whole number.”

$3$ is in the ones place, so look at the next digit: $4$.
It isn’t $5$ or higher, so don’t round up. Thus, $123.456$ rounds to $123$[.]

Word Problems

Word problems scare a lot of people, but fear not! Here is a list of operations and the words associated with them that you’ll commonly find in a word problem.

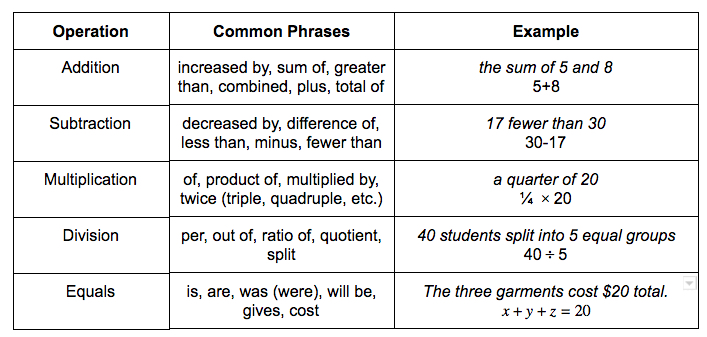
When solving a word problem, it’s very helpful to identify a variable first. The variable is the unknown amount, usually represented by a letter. Let’s look at this word problem:

“One-third of all the students are left-handed. If $20$ students are left-handed, how many total students are there?”

Step 1: Identify the variable. Usually, look at the last part of a word problem to help. In this case, we are looking for total students. Let s = total students.

Step 2: Translate words into math: “One third of all students are left handed” becomes $\frac{1}{3} \cdot s = 20$

Step 3: Solve the equation. For this, reference the next section. In this particular case, the answer is $s = 60$ students*.

Note that a constant is any number that is fixed and not variable, such as $2$ or $10$.

Solving Linear Equations

It’s important to know that an equation is like a scale, so if you do something to one side of the equation, you should do it to the other side, too, in order to keep it balanced. You can add/subtract/multiply/divide whatever you want from/to both sides of any equation and it’ll still be true.

Example, if $x + 5 = 3$ is true, and you add $2$ to both sides, then $x + 7 = 5$ is true as well. In this case, adding $2$ wasn’t really a wise choice if you wanted to solve the equation (find what $x$ equals).

To solve a linear equation, isolate the variable by performing the inverse operation to both sides of the equation. Here are some examples of this process.

Addition

Example: $x + 5 = 12$ (the inverse operation of “+ 5” is “– 5”, so let’s subtract 5 from both sides.)

$x + 5 - 5 = 12 - 5$ and $5-5=0$ so the left side becomes $x + 0$ which is just x. And on the right side, $12 - 5 = 7$, so that is your answer: $x = 7$.

Subtraction

Example: $z - 3 = –4$ (The inverse operation of “$–3$” is “$+ 3$”, so let’s add $3$ to both sides.)

$z-3+3=-4+3$ (Subtracting $3$ from $z$ and then adding it back gets you right back to $z$.)
$z = -1$

Multiplication

Example: $3 \cdot y = 15$ (The inverse operation of $\cdot 3$ is $\div 3$, so divide both sides by $3$.)

$3 \cdot y \div 3 = 15 \div 3$ ($y$ is multiplied by $3$ and then divided by $3$, so it is unchanged.)
$y = 5$

Sometimes, you’ll have a multiplication problem with a fraction, like the example from the word problem: $\frac{1}{3}s = 20$
In these cases, while you can divide both sides by $3$, it’s easiest to multiply both sides of the equation by the reciprocal. (Note: $\frac{1}{3} \cdot \frac{3}{1} = \frac{3}{3} = 1$)

\[\frac{1}{3} \cdot s \cdot \frac{3}{1} = 20 \cdot \frac{3}{1}\] \[s = 60\]

Division

Example: $\frac{y}{8} = 10$ (The inverse operation of $\div 8$ is $\cdot 8$, so let’s multiply both sides by $8$.)

\[(\frac{y}{8}) \cdot 8 = 10 \cdot 8\] \[y=80\]