Formulas You Need to Know for the ACT Math Test

The ACT® (American College Testing) Math Test has 60 questions that cover a wide range of topics covered in high school. If you don’t remember your high school math classes, don’t worry! We’ve compiled the essential formulas you’ll need to know for the ACT Math Test. Even if you are not allowed to use this formula chart during the text, it’s a great tool for studying. Also, remember that in some cases, you’ll be allowed to use a calculator during your test, so you can remember the formulas and just plug in the values in your calculator.

Feel free to practice solving the problems on our sample ACT Math Test, and check out our study guide for the ACT Math section at Union Test Prep if you want more details.

Exponents

Formula	Symbols
\(x^a \cdot x^b = x^{a+b}\)	\(a, b, x =\text{any real number}\)
\(\dfrac{x^a}{x^b}=x^{a-b}\)	\(a, b, x =\text{any real number}\)
\((x^a)^b=x^{a \cdot b}\)	\(a, b, x =\text{any real number}\)
\((x \cdot y)^a=x^a \cdot y^a\)	\(a, x, y =\text{any real number}\)
\(x^1=x\)	\(x= \text{any real number}\)
\(x^0 = 1\)	\(x = \text{any real number}\)
\(x^{-a} = \dfrac{1}{x^a}\)	\(a,x = \text{any real number}\)
\(x^{\frac{a}{b}} = \sqrt[b]{x^a} = (\sqrt[b]{x})^a\)	\(a, b, x = \text{any real number}\)

Statistics

Formula	Symbols
\(p = \dfrac{d}{t}\)	\(p = \text{probability of an event}\) \(d = \text{desired event}\) \(t= \text{total number of possible events}\)
\(\bar{x} = \dfrac{\sum{x_i}}{n}\)	\(\bar{x} = \text{mean}\) \(x_i = \text{value of each measurement}\) \(n = \text{number of measurements}\)
\(s = \sqrt{\mathstrut \dfrac{\sum(x_i - \bar{x})^2}{n-1}}\)	\(s = \text{standard deviation}\) \(\bar{x}=\text{mean}\) \(x_i = \text{value of each measurement}\) \(n = \text{number of measurements}\)
\(V = s^2\)	\(V = \text{variance}\) \(s = \text{standard deviation}\)
\(CV = RSD = 100 \cdot \dfrac{s}{\bar{x}}\)	\(CV = \text{coefficient of variation}\) \(RSD = \text{relative standard deviation}\) \(s = \text{standard deviation}\) \(\bar{x} = \text{mean}\)

Linear Equations

Formula	Symbols	Comments
\(A\cdot x + B\cdot y = C\)	\(A, B, C = \text{any real number}\) \(y= \text{dependent variable}\) \(x = \text{independent variable}\)	Standard Form
\(y=m \cdot x + b\)	\(y = \text{dependent variable}\) \(m= \text{slope}\) \(x = \text{independent variable}\) \(b = y \text{-intercept}\)	Slope-Intercept Form. Try to convert linear equations to this format.
\(m = \dfrac{y_2 - y_1}{x_2 - x_1}\)	\(m = \text{slope}\) \(y_n = \text{dependent variable (point n)}\) \(x_n = \text{independent variable (point n)}\)	This is a rearranged version of the point-slope form.
\(y-y_1 = m(x-x_1)\)	\(y= \text{dependent variable}\) \(x = \text{independent variable}\) \(y_1 = y \text{ value of a point on the line}\) \(x_1 = x \text{ value of a point on the line}\) \(m = \text{slope}\)	Point-Slope form
\(x+a = b \Rightarrow x = b-a\) \(x-a = b \Rightarrow x = b+a\) \(x \cdot a = b \Rightarrow x = b \div a\) \(x \div a = b \Rightarrow x = b \cdot a\) \(x^a = b \Rightarrow x = \sqrt[a]{b}\) \(\sqrt[a]{x} = b \Rightarrow x = b^a\) \(a^x = b \Rightarrow x = \dfrac{\log b}{\log a}\)	\(a, b = \text{constants}\) \(x = \text{variable}\)

Quadratic Equations

Formula	Symbols	Comments
\(x= \frac{-b \pm \sqrt{b^2-4ac}}{2a}\)	\(a,b = \text{constants}\) \(c = \text{constant (y-intercept)}\) \(x = \text{variable}\)	Quadratic Formula for equation in the form \(ax^2+bx+c=0\)
\((a \pm b)^2 = a^2 \pm 2ab + b^2\)	\(a,b = \text{constants or variables}\)	Square of a sum or difference
\(a^2-b^2 = (a+b)\cdot (a-b)\)	\(a,b = \text{constants or variables}\)	Difference of squares

Cubic Equations

Formula	Symbols	Comments
\(a^3-b^3 = (a-b) \cdot (a^2+ab + b^2)\)	\(a,b = \text{constants or variables}\)	Difference of cubes
\(a^3+b^3 = (a+b) \cdot (a^2-ab + b^2)\)	\(a,b = \text{constants or variables}\)	Sum of cubes

Sequences and Patterns

Formula	Symbols	Comment
\(a_n=a_1+(n-1) \cdot d\)	an = value of the nth term a1 = first term n = any number in the series d = difference b/w consecutive terms	This formula is for an arithmetic sequence
\(s_n=\frac{n \cdot (a_1 + a_n)}{2}\)	sn = sum of sequence with n terms an = value of the nth term a1 = first term n = any number in the series	This formula is for an arithmetic sequence
\(r = \frac{a_2}{a_1} = \frac{a_n}{a_{(n-1)}}\)	r = ratio in a geometric sequence a1 = first term a2 = second term an = value of the nth term	This formula is for a geometric sequence
\(a_n=a_1 \cdot r^{n-1}\)	r = ratio in a geometric sequence a1 = first term n = any number in the series an = value of the nth term	This formula is for a geometric sequence
\(s_n = \frac{a_1 \cdot (1-r^n)}{1-r}\)	r = ratio in a geometric sequence a1 = first term n = any number in the series sn = sum of sequence with n terms	This formula is for a geometric sequence

Functions

Formula	Symbols	Comment
\((f+g)(x) = f(x) + g(x)\)	\(f(x) = \text{function } f\) \(g(x) = \text{function } g\)	Addition of Functions
\((f-g)(x) = f(x) - g(x)\)	\(f(x) = \text{function } f\) \(g(x) = \text{function } g\)	Subtraction of Functions
\((f \cdot g)(x) = f(x) \cdot g(x)\)	\(f(x) = \text{function } f\) \(g(x) = \text{function } g\)	Multiplication of Functions
\((\frac{f}{g})(x) = \frac{f(x)}{g(x)}\)	\(f(x) = \text{function } f\) \(g(x) = \text{function } g\)	Division of Functions
\((f \circ g)(x) = f(g(x))\)	\(f(x) = \text{function } f\) \(g(x) = \text{function } g\)	Composition of Functions

Geometry Equations

Formula	Symbols	Comments
\(A = s^2\)	\(A = \text{area of a square}\) \(s = \text{side length}\)
\(A = l \cdot w\)	\(A = \text{area of a rectangle}\) \(l = \text{length}\) \(w = \text{width}\)
\(A = \dfrac{1}{2} b \cdot h\)	\(A = \text{area of a triangle}\) \(b= \text{base}\) \(h = \text{height}\)
\(A = \pi \cdot r^2\)	\(A = \text{area of a circle}\) \(r = \text{radius}\)
\(A = h \cdot \dfrac{b_1+b_2}{2}\)	\(A = \text{area of a trapezoid}\) \(b_n = \text{base }n\) \(h = \text{height}\)
\(C= 2 \pi r = \pi d\)	\(C = \text{perimeter of a circle}\) \(r = \text{radius}\) \(d = \text{diameter}\)
\(V = s^3\)	\(V = \text{volume of a cube}\) \(s = \text{side length}\)
\(V = l \cdot w \cdot h\)	\(V = \text{volume of a rectangular prism}\) \(l = \text{length}\) \(w = \text{width}\) \(h = \text{height}\)
\(V = \dfrac{4}{3} \pi r^3\)	\(V = \text{volume of a sphere}\) \(r = \text{radius}\)
\(V = \pi r^2 h\)	\(V = \text{volume of a cylinder}\) \(r = \text{radius of base}\) \(h = \text{height}\)
\(V = \dfrac{1}{3} \pi r^2 h\)	\(V = \text{volume of a cone}\) \(r = \text{radius}\) \(h = \text{height}\)
\(V = \dfrac{1}{3} l \cdot w \cdot h\)	\(V = \text{volume of a pyramid}\) \(l = \text{length}\) \(w = \text{width}\) \(h = \text{height}\)
\(d= \sqrt{\mathstrut (y_2 - y_1)^2 + (x_2-x_1)^2}\)	\(d = \text{distance between two points}\) \(y_n = y \text{ value at point n}\) \(x_n = x \text{ value at point n}\)
\(a^2 + b^ 2 = c^ 2\)	\(a,b = \text{legs of a right triangle}\) \(c = \text{hypotenuse of a right triangle}\)	Pythagorean theorem
\((x-h)^2 + (y-k)^2 = r^2\)	\((h,k) = \text{center of a circle}\) \(r = \text{radius}\)	Standard form of a circle
\(x^2 + y^2 + Ax + By + C = 0\)	\(x, y = \text{variables}\) \(A,B,C = \text{constants}\)	General form of a circle

Trigonometry Equations

Formula	Symbols	Comments
\(\sin^2 \theta + \cos^2 \theta = 1\)		Pythagorean Identity
\(\sin 2\theta = 2 \sin \theta \cdot \cos \theta\) \(\cos 2\theta = \cos^2 \theta - \sin^2 \theta = 2 \cos^2 \theta -1\) \(\tan 2\theta = \frac{2 \tan \theta}{1-\tan^2 \theta}\)		Double Angle formulas

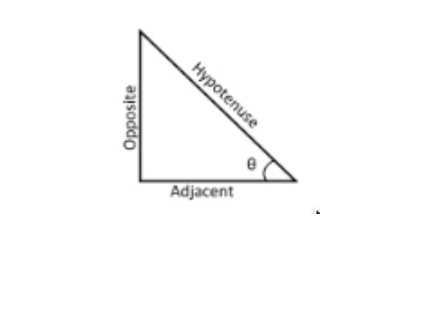
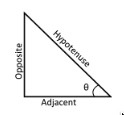
Formulas with Diagrams

\[\sin \theta = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{1}{\csc \theta} \\ \cos \theta = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{1}{\sec \theta} \\ \tan \theta = \frac{\sin \theta}{\cos \theta} =\frac{\text{opposite}}{\text{adjacent}} = \frac{1}{\cot \theta}\]

\[\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} \\ a^2 = b^2 + c^2 -2bc \cos A \\ b^2 = a^2 + c^2 -2ac \cos B \\ c^2 = a^2 + b^2 -2ab \cos C\]