Mathematics Study Guide for the TEAS

Numbers: Part 2

Operations with Rational Numbers

Any number that can be written as a quotient of two integers is a rational number. That includes numbers like $\frac{3}{5}, \frac{7}{11},$ or$\frac{-24}{17}$. Keep in mind that the definition says “can be written” as a quotient, so numbers that are integers, like maybe $8$ or $-11$ are rational because they can be written as $\frac{8}{1}$ or $\frac{-11}{1}$.

Order of Operations

When solving expressions that involve two or more operations, the order in which the operations are performed is guided by a specific sequence known as the order of operations. This sequence is commonly abbreviated using the acronym PEMDAS: Parentheses, Exponents, Multiplication and Division (in order, left to right), and Addition and Subtraction (in order, left to right).

The mnemonic Please Excuse My Dear Aunt Sally is often used as an easy way to remember the acronym.

If the order of operations is not used, the same problem can render two or more completely different answers.

For example, one might naturally assume $2 + 3 \cdot 4 = 20$, given that $2 + 3 = 5$, and $5 \cdot 4 = 20$.

Yet, if two is added to (three multiplied by four), the result is $2 + (3 \cdot 4) = 2 + 12 = 14$, which is the correct answer. This illustrates the importance of the order of operations.

Positive and Negative Numbers

Positive numbers are also known as non-negative numbers. The term positive conveys the idea that their values are greater than zero. Positive whole numbers are essentially counting numbers.

Negative numbers are those numbers whose values are less than zero. They are, therefore, located to the left of zero on the number line. In most cases, they are preceded by a minus sign. However, in certain contexts, such as on spreadsheets and some bank statements, their negative status is designated by the color red, by enclosing them in parentheses, or both.

2 Integer Number Line.png

Adding

Adding a group of all negative numbers is carried out by initially adding them as if they were positive, and then labeling the resulting sum with a minus sign.

To add a combination of negative and positive numbers, first add the two types of numbers separately. Then subtract the smaller sum from the larger sum and label the resulting difference with the sign that matches the larger sum. Hence:

\[–8 + 3 + 7 + (–9) =\; –17 + 10 = \;–7\]

Subtracting

To solve a subtraction problem involving a negative number or negative numbers, reverse the sign of the number that is being subtracted and then add. For example:

\[–8 \,–( +4) = \;–8 + (–4) = \;–12\] \[–9\, – (–3) =\; –9 + 3 =\; –6\] \[5\, – (–6) = 5 + 6 = 11\]

Multiplying

The product of a negative number and another negative number is positive, so:

\[–8 \;\cdot \;–3 = 24\]

The product of a negative number and a positive number is negative, thus:

\[–8 \cdot 3 = \;–24\]

If you are asked to multiply a series of negative and positive numbers, you can shorten the process by first multiplying the numbers and disregarding the signs. Then, add the sign according to the number of negative signs in the original group.

If the number of negative signs is even, the answer will be positive.
If the number of negative signs is odd, the answer will be negative.

So:

\[(-3)(4)(2)(-5) = 120\]

But:

\[(-3)(4)(-2)(-5) = -120\]

Dividing

The quotient of a negative number divided by another negative number is positive, so:

\[–24 \;\div \;–8 = 3\]

However, the quotient of a negative number divided by a positive number (or vise versa) is negative, hence:

\[–24 \div 8 =\; –3\]

Operations with Fractions

Everything you know about operations with integers is still true with fractions, but operations with fractions generally involve more steps. As you may remember, and will see below, adding and subtracting fractions requires that the fractions have the same denominator. This isn’t true for multiplying and dividing. In every operation, it’s always good practice to simplify the result to the lowest terms.

Adding and Subtracting

To add or subtract fractions with like denominators, add or subtract the numerators as usual and leave the denominator as is. Simplify, if necessary.

\[\frac{5}{16} + \frac{7}{16} = \frac{12}{16} = \frac{3}{4}\] \[\frac{9}{12} - \frac{5}{12} = \frac{4}{12} = \frac{1}{3}\]

To add or subtract fractions with different denominators, first, rewrite the problem using equivalent fractions that share the same (least) common denominator. Then proceed as usual.

\[\frac{3}{4} + \frac{1}{6}\] \[\frac{9}{12} + \frac{2}{12} = \frac{11}{12}\]

Multiplication

To multiply fractions, multiply their numerators by one another. The resulting product serves as the numerator in the answer. Then multiply their denominators by one another as well, and use the resulting product as the answer’s denominator. Remember to simplify the answer to lowest terms, if applicable.

\[\frac{1}{7} \cdot \frac{2}{9} = \frac{1 \cdot 2}{7 \cdot 9} = \frac{2}{63}\] \[\frac{2}{6} \cdot \frac{4}{8} = \frac{8}{48} = \frac{8 \div 8}{48 \div 8} = \frac{1}{6}\]

Division

To divide fractions, multiply the dividend by the reciprocal of the divisor by flipping the second fraction upside down and then following the usual steps for multiplying fractions. Again, simplify to lowest terms if appropriate.

\[\frac{6}{8} \div \frac{1}{4} = \frac{6}{8} \cdot \frac{4}{1} =\frac{24}{8} = \frac{3}{1} = 3\]

Operations with Mixed Numbers

To do operations with mixed numbers, it’s almost always necessary to rewrite them as improper fractions, which have been described earlier in this guide. For example, what is $3\frac{5}{8}$ written as an improper fraction?

The method is this: If the mixed number is $a\frac{b}{c}$, the improper fraction is $\frac{ac+b}{c}$. For example:

\[3\frac{5}{8} = \frac{3 \cdot 8 + 5}{8} = \frac{29}{8}\]

Simplifying or Reducing to Lowest Terms

If you are asked to simplify a fraction or write it in lowest terms, you’ll need to find the greatest common factor of the numerator and denominator. This is the largest number by which both the numerator and denominator can be evenly divided. For example, to simplify the fraction $\frac{24}{36}$, do this:

The factors of $24$ are $1, \,2,\, 3, \,4, \,6, \,8, \,12, \,24$.
The factors of $36$ are $1,\, 2, \,3,\, 4,\, 6, \,9,\, 12, \,18,\, 36$.

The greatest factor of both numbers is $12$, so divide the numerator and denominator by $12$ to reduce the fraction:

\[\frac{24 \div 12}{36 \div 12} = \frac{2}{3}\]

Operations with Decimals

You should be able to do the same basic four operations with decimal numbers that you can do with integers or fractions.

Adding and Subtracting

To add or subtract decimals, position their digits one above the other so that all corresponding place values are aligned. If desired, insert zeros so the numbers are all the same length as well. Then add or subtract using column addition or subtraction as normal, making sure to maintain the decimal point in the same position in the resulting sum or difference.

So, $13.1594 + 0.217$ would be written:

\[\begin{array}{r} &13.1594\\ +\!\!\!\!\!\!&0.2170\\ \hline &13.3764 \end{array}\]

Multiplying

To multiply decimals, begin by multiplying the numbers as usual, ignoring all decimal points. Then count the combined number of decimal places in the numbers you multiplied, and insert a decimal point in the product such that the number of decimal places in the answer matches the total number of decimal places you counted. For example:

\[1.2 \times 0.11 = 0.132\]

First, rewrite vertically:

\[\begin{array}{r} &1.2\\ \times\!\!\!\!\!\!&0.11\\ \hline &12 \\ &12\phantom{2}\\ \hline &132 \end{array}\]

There are a total of three decimal points in the two numbers being multiplied, so move the decimal point three spaces to the left, after finding the numerical answer. That gives $0.132$.

Dividing

To divide decimal numbers, if there is a decimal point in the divisor, move it all the way to the right. Then move the decimal point in the dividend to the right that same number of places. Finish by dividing, as usual, remembering to insert the decimal point in the quotient directly above the decimal point in the dividend. This would mean that $81\div 0.9$ can be rewritten vertically, like this:

\[\require{enclose} \begin{array}{r} 0.9 \enclose{longdiv}{81} \\[-3pt] \end{array}\]

Move the decimal point to the right of the $9$, and, correspondingly, one place to the right in the dividend, adding a $0$ to make this possible. Then, solve as regular long division, being sure to place the quotient’s decimal point directly above the decimal point in the dividend.

\[\require{enclose} \begin{array}{r} 90. \\[-3pt] 09. \enclose{longdiv}{810.} \\[-3pt] \underline{81}\phantom{0.} \\[-3pt] \phantom{1} 0 \\[-3pt] \phantom{1} \underline{0} \end{array}\]

Operations with Percentages

To add or subtract percentages, simply combine or subtract them as you would any number, making sure that digits in corresponding places are aligned, so $12\% \,– 5\% = 7\%$.

To add or subtract a given percentage to or from a number, multiply the number by the percent’s decimal equivalent and then add or subtract the result from the original number, as appropriate. That means the cost of a $\$65$ item that is marked $40\%$ off would be $65\, – (65 \cdot 0.40) = 39$, or $\$39.00$.

Comparing and Ordering Rational Numbers

Be able to use the symbols $<, \,>, \,\leq,$ and $\geq$ to compare rational numbers and to order a set of numbers, either ascending or descending. Just as you know that $19$ is larger than $7$ and can write $19>7$, you also need to be able to determine that a rational number such as $\frac{7}{8}$ is larger than $\frac{2}{3}$ and write $\frac{7}{8} > \frac{2}{3}$.

Decimals

To determine the correct arrangement when putting numbers in sequential order, position their digits one below the other so that their corresponding place values are aligned. Then compare their values column by column, moving from left to right.

10.407
10.0407

Evaluating each place, beginning at the left, we can see that the two numbers are equal until we reach the tenths place. Then, it becomes obvious which number is greater: the top one is larger because it has a 4 in the tenths place, while the bottom number contains a 0 in that place.

The largest number is the number whose leftmost digit has the greatest value. The second largest is the one whose leftmost digit has the second greatest value, and so on. If two or more digits have the same value, find the larger number by comparing the digits in the column that immediately follows. This manner of ordering numbers applies both to whole numbers and decimal numbers.

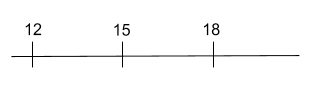
Another method of ordering numbers is to compare their positions on a number line. Here, the values increase as one moves from left to right. To find numbers that are not marked on a number line, approximate their location by evaluating where they are most likely positioned, relative to values that are marked.

For example, you could determine approximately where 16.5 would fall on this number line, even though that value is not specifically marked. It would be halfway between 15 and 18.

3 Number Line Number Comparison.png

Fractions

The order of fractions that have the same denominator can be determined by ignoring their denominators and arranging them in accordance with the values of their numerators.

The fractions $\frac{3}{11}, \frac{1}{11}, \frac{7}{11}$ would be ordered in sequence like this:

\[\frac{1}{11}, \frac{3}{11}, \frac{7}{11}\]

If the denominators are not the same, you will need to create equivalent fractions with the same denominator before comparing them, like this:

\[\frac{3}{4}, \frac{2}{3}, \frac{1}{2}\]

These become:

\[\frac{9}{12}, \frac{8}{12}, \frac{6}{12}\]

Then, they are easily compared by placing the numerators in order of value:

\[\frac{6}{12}, \frac{8}{12}, \frac{9}{12}\]

A quick way to compare two fractions whose denominators are not the same is to cross-multiply. Multiply the numerator of the first fraction by the denominator of the second fraction and write the resulting product next to the first fraction. Then multiply the numerator of the second fraction by the denominator of the first fraction and write the resulting product next to the second fraction. The larger product identifies the fraction with the greater value.

For example:

Compare $\frac{3}{8}$ and $\frac{1}{3}$

$(9) \frac{3}{8}$ and $\frac{1}{3} (8)$

So, $\frac{3}{8} \gt \frac{1}{3}$

Equivalent Fractions

There are an infinite number of ways to express a fraction; for example, $\frac{1}{2}$ is the same as $\frac{2}{4}$, $\frac{3}{6}$, $\frac{4}{8}$, and so on. To find an equivalent fraction, simply multiply or divide the numerator and denominator by the same number. This works accurately because you are multiplying or dividing by $\frac{2}{2}$, $\frac{3}{3}$, $\frac{4}{4}$, etc., and these numbers are all equal to $1$. This knowledge can be very useful when you do operations with fractions or reduce them to lowest terms.

Comparing a Variety of Number Types

The easiest way to compare numbers is to have them in the same form, for example, all in decimals or in fractions. If in fractions, it’s easiest if they have the same denominator. If you have to deal with several different number types, it’s generally easiest if you change them all to decimals.

Estimation and Rounding

Sometimes, all that is called for is an answer that isn’t exact, but is close. We can skip a detailed calculation and estimate the answer. This almost always is going to involve rounding numbers. Instead of using $975$ you might use a simpler number like $1\text{,}000$ that’s close enough for an estimate. See below for more on this.

Estimation

A good habit to adopt whenever you have to carry out a calculation is to form an idea as to what a sensible answer might be. In other words, you should use estimation to gauge whether the answer you found makes sense based on the context of the problem. You can, of course, use rounding to make the numbers easier to work with, but be careful not to use too many estimated or rounded numbers. You won’t end up with a logical answer.

Example:

You’re headed to see a movie where the admission charge is $\$8.75$. You know that a large drink is going to be $\$5.29$ and buttered popcorn is $\$4.79$. To be sure that you have enough cash, you do a quick estimate by rounding each price to the nearest dollar and adding them: $9+5+5=19$. So, to be safe, a twenty-dollar bill should do the job. (We’re ignoring any sales tax.)

Example:

Max found $61$ firecrackers in a drawer and promptly set off $29$ of them. He wants to divide the rest among three friends. What is a quick estimate for how many firecrackers each friend will get? We could round $61$ to $60$ and $29$ to $30$. Subtracting these rounded numbers, Max has $60-30 = 30$ firecrackers left. Dividing that number, Max gives $30 \div 3 = 10$ firecrackers for each friend. (The exact answer would be $10.7$, so our estimate is quite close.)

Rounding

Rounding numbers to a given place value is a way of estimating that is often used to make numbers easier to work with, such as rounding to the nearest 10 or rounding to the hundreds place. It can also be an effective way to check to see if your answer to a problem with confusing numbers is reasonable—but be careful not to round too much. You will want to round to the nearest number so that you can accurately check your work.

Example:

Round $3.14159$ to the nearest thousandth.

The thousandths place is the third place to the right of the decimal. That digit is $1$. Now look at the next digit to the right. Is it $5$ or greater? If yes, then round the $1$ up to $2$.

That gives us 3.142 after we drop the $59$. If the digit to the right had not been $5$ or greater, we would have kept the $1$ digit.

The process goes like this for rounding to the right of the decimal point.

Find the decimal place (your target) that needs to be rounded.
Look to the immediate right of the target.
If the number to the right is $5$ or greater, add $1$ to the target and drop the rest of the digits to the right.

The process goes like this for rounding to the left of the decimal point.

Find the place (your target) that needs to be rounded.
Look to the immediate right of the target.
If the number to the right is $5$ or greater, add $1$ to the target and make every digit to the right of the target a 0.

Example:

Round $409$ to the nearest ten. The tens place (the $0$) is the target and the number to the right of the target is $9$. Since $9$ is greater than $5$, add $1$ to the $0$. Make the $9$ a $0$.

Answer: $410$

Example:

Working with money:

At a rate of $1.21 \%$ for a certain time period, what would the interest be on $\$65$?

Multiply $.0121 \times \$65.00 = \$.7865$. Even though that’s all correct, we can only collect cash to the nearest cent. So how do we round our answer?

Round to the nearest cent (hundredth). The target is $8$. To the right of the $8$ there is a $6$, so we add $1$ to the $8$ and drop the $65$ part.

Answer: $\$ 0.79$.