Formulas for Math on the ParaPro Test: Part 2—Geometry and Measurement

Geometry and measurement are areas of Math where students tend to struggle a lot. If you’re studying for the ParaPro Math Test, then you’re going to be asked about how to determine areas, perimeters, volumes… and how to teach them to your students, so you’ll need to dominate the formulas first.

That’s why we’ve prepared a formula chart with the geometry and measurement formulas you’ll need if you want to ace the ParaPro Test and teach the subject you love! You’ll also need these two formula charts for some questions:

Formulas for ParaPro Number Sense and Algebra Questions

Formulas for ParaPro Data Analysis Questions

Also, check out our mathematics study guide for more in-depth information about each formula. Ready to test your knowledge? Try our mathematics practice questions and flashcards.

Geometry and Measurement Formulas for the ParaPro Test

Category	Formula	Symbols	Comment
Geometry and Measurement	\(Du = Su \cdot \dfrac{Du}{Su} = Su \cdot CF\)	\(Du =\) Desired Unit \(Su =\) Starting Unit \(CF =\) Conversion Factor	Multiple Steps may be needed
Geometry and Measurement	\(P = 4 \cdot s\)	\(P =\) Perimeter of a square \(s=\) side length
Geometry and Measurement	\(P = 2l + 2w\)	\(P =\) Perimeter of a rectangle \(l =\) length \(w =\) width
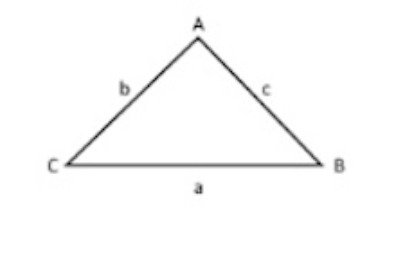
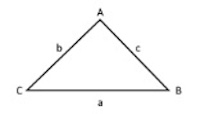
Geometry and Measurement	\(P = s_1 + s_2 + s_3\)	\(P =\) Perimeter of a triangle \(s_n =\) side length
Geometry and Measurement	\(C = 2 \cdot \pi \cdot r = \pi \cdot d\)	\(C =\) Perimeter of a circle \(r =\) radius \(d =\) diameter \(\pi \approx 3.14\)
Geometry and Measurement	\(s = r \cdot \theta\)	\(s =\) arc length \(r =\) radius \(\theta =\) central angle (radians)
Geometry and Measurement	\(A = s^2\)	\(A =\) Area of a square \(s =\) side length
Geometry and Measurement	\(A = l \cdot w\)	\(A =\) Area of a rectangle \(l =\) length \(w =\) width
Geometry and Measurement	\(A = \frac{1}{2}bh\)	\(A =\) Area of a triangle \(b =\) base \(h =\) height
Geometry and Measurement	\(A = \pi \cdot r^2\)	\(A =\) Area of a circle \(r =\) radius
Geometry and Measurement	\(A = h \cdot \dfrac{b_1 +b_2}{2}\)	\(A =\) Area of a trapezoid \(b_n =\) base n \(h =\) height
Geometry and Measurement	\(V = s^3\)	\(V =\) Volume of a cube \(s =\) side length
Geometry and Measurement	\(V = l\cdot w \cdot h\)	\(V =\) Volume of a rectangular prism \(l =\) length \(w =\) width \(h =\) height
Geometry and Measurement	\(V= \frac{4}{3} \cdot \pi \cdot r^3\)	\(V =\) Volume of a sphere \(r =\) radius
Geometry and Measurement	\(V = \pi \cdot r^2 \cdot h\)	\(V =\) Volume of a cylinder \(r =\) radius \(h =\) height
Geometry and Measurement	\(V = \frac{1}{3} \cdot \pi \cdot r^2 \cdot h\)	\(V =\) Volume of a cone \(r =\) radius \(h =\) height
Geometry and Measurement	\(V = \frac{1}{3} lwh\)	\(V =\) Volume of a pyramid \(l =\) length \(w =\) width \(h =\) height
Geometry and Measurement	\(SA = \Sigma A_{fi}\)	\(SA =\) Surface Area of a Prism \(A_{fi} =\) Area of face i
Geometry and Measurement	\(SA = \Sigma A_{fi}\)	\(SA =\) Surface Area of a Pyramid \(A_{fi} =\) Area of face i
Geometry and Measurement	\(SA = 2B + C\cdot h\)	\(SA =\) Surface Area of a Cylinder \(B =\) Area of the Base \(C =\) Circumference of the Base \(h =\) height
Geometry and Measurement	\(SA = B + \frac{1}{2} \cdot C \cdot l\)	\(SA =\) Surface Area of a Cone \(B =\) Area of the Base \(C =\) Circumference of the Base \(l =\) slant height
Geometry and Measurement	\(SA = 4 \pi r^2\)	\(SA =\) Surface Area of a Sphere \(r =\) radius of the sphere
Geometry and Measurement	\(d = \sqrt{(y_2 - y_1)^2 + (x_2 - x_1)^2}\)	\(d =\) distance between two points \(y_n =\) y score at point n \(x_n =\) x score at point n
Geometry and Measurement	\(a^2 + b^2 = c^2\)	\(a,b =\) legs of a right triangle \(c =\) hypotenuse of a right triangle
Geometry and Measurement	\((x-h)^2 + (y - k)^2 = r^2\)	\((h,k) =\) center of a circle \(r =\) radius	Standard form of a circle
Geometry and Measurement	\(x^2 + y^2 + Ax + By + C = 0\)	\(x,y =\) variables \(A, B, C =\) constants	General form of a circle
Geometry and Measurement	\(\cos ^2 \theta + \sin ^2 \theta = 1\)
Geometry and Measurement	\(\sin 2\theta = 2 \cdot \sin \theta \cdot \cos \theta\)
Geometry and Measurement	\(\cos 2 \theta = \cos ^2 \theta - \sin ^2 \theta = 2 \cos ^2 \theta - 1\)
Geometry and Measurement	\(\tan (2\theta) = \dfrac{ 2 \tan \theta}{1-\tan ^2 \theta}\)

Formulas Requiring Graphics

\[\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}\] \[a^2= b^2 +c^2 - 2bc \cos A\] \[b^2 = a^2 + c^2 - 2ac \cos B\] \[c^2 = a^2 + b^2 - 2ab \cos C\]