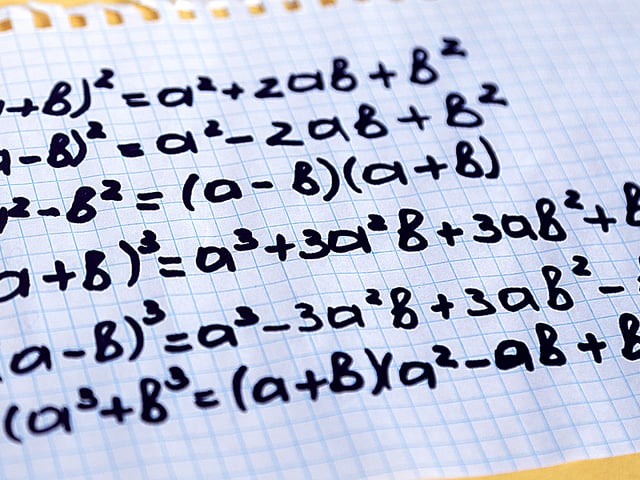
Algebra Formulas You Need to Know for the HiSET® Math Test

You will be given some formulas during the HiSET® Math Test, but those formulas are not going to be all the formulas you’ll need. But don’t worry—we have you covered. The following chart shows the algebra formulas you need to know, but won’t be given, during the test—compiled for you by the Union Test Prep team.

We also have two other charts of formulas that are not given to you during the test and a preview of the chart of formulas you will be given during the HiSET Math Test session.

Geometry Formulas You Need to Know for the HiSET® Math Test

Formulas You Will Be Given for the HiSET® Math Test

Statistics and Probability Formulas You Need to Know for the HiSET® Math Test

Algebra Formulas for the HiSET® Math Test

Category	Formula	Symbols	Comment
General Algebra	\(x+a=b \Rightarrow x=b-a\) \(x-a=b \Rightarrow x=b+a\) \(x \cdot a=b \Rightarrow x=b \div a\) \(x \div a=b \Rightarrow x=b \cdot a\) \(x^a=b \Rightarrow x = \sqrt[a]{b}\) \(\sqrt[a]{x}= b \Rightarrow x= b^a\) \(a^x=b \Rightarrow x=\frac{log\ b}{log\ a}\)	a, b = constants x = variable
General Algebra	\(x^a \cdot x^b = x^{a+b}\)	a, b, x = any real number
General Algebra	\(\frac{x^a}{x^b}=x^{a-b}\)	a, b, x = any real number
General Algebra	\((x^a)^b = x^{a \cdot b}\)	a, b, x = any real number
General Algebra	\((x \cdot y)^a = x^a \cdot y^a\)	a, b, x = any real number
General Algebra	\(x^1 = x\)	x = any real number
General Algebra	\(x^0 = 1\)	x = any real number
General Algebra	\(x^{-a} = \frac {1}{x^a}\)	a, x = any real number
General Algebra	\(x^{\frac {a}{b}} = \sqrt[b]{x^a} = (\sqrt[b]{x})^a\)	a, b, x = any real number
Linear Equations	\(A \cdot x + B \cdot y = C\)	A, B, C = any real number y = dependent variable x = independent variable	Standard form
Linear Equations	\(y = m \cdot x + b\)	y = dependent variable m = slope x = independent variable b = y axis intercept	Slope-intercept form Try to convert any linear equation to this form.
Linear Equations	\(m = \frac{(y_2 - y_1)}{(x_2 - x_1)}\)	m = slope \(y_n\) = independent variable (point n) \(x_n\) = dependent variable (point n)	This is a rearrangement of the point-slope form.
Linear Equations	\(y-y_1 = m(x-x_1)\)	\((x_1,y_1)\) = point on the line m = slope y = independent variable x = dependent variable	Point-slope form
Quadratic Equations	\(x= \frac{-b \pm \sqrt{b^2-4 \cdot a \cdot c}}{2 \cdot a}\)	a, b, c = constants c = y axis intercept x = variable	Standard form
Quadratic Equations	\((a \pm b)^2 = a^2 \pm 2 \cdot a \cdot b + b^2\)	a, b = constants or variables	Square of a sum or difference
Quadratic Equations	\(a^2 - b^2 = (a-b) \cdot (a+b)\)	a, b = constants or variables	Difference of two squares
Cubic Equations	\(a^3 - b^3 = (a-b) \cdot (a^2+ab+b^2)\)	a, b = constants or variables	Difference of two cubes
Cubic Equations	\(a^3 + b^3 = (a+b) \cdot (a^2-ab+b^2)\)	a, b = constants or variables	Sum of two cubes
Sequences	\(a_n = a_{n-1} + d\)	\(a_n = n^{th}\) term of arithmetic sequence \(a_{n-1} = (n-1)^{th}\) term of arithmetic sequence \(d\) = common difference
Sequences	\(a_n = a_{n-1} \cdot r\)	\(a_n = n^{th}\) term of geometric sequence \(a_{n-1} = (n-1)^{th}\) term of geometric sequence \(r\) = common ratio