Mathematics Knowledge Study Guide for the ASVAB

Geometry: Part 3

Solid Geometry

In considering three dimensional objects, we encounter the concepts of volume and surface area. We will take a look at rectangular right prisms (box-shaped) and cylinders.

Formulas for Volume and Surface Area

Volume units will most likely be cubic units, such as \(cm^3\) or \(ft^3\). Surface area units will be square units, such as \(m^2\) or \(in^2\).

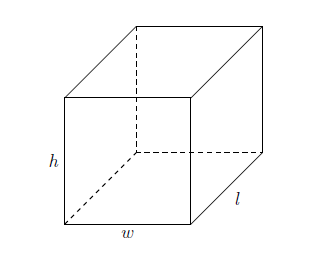
Rectangular Solid

In a rectangular right prism with dimensions length = \(l\), width = \(w\), and height = \(h\), the volume can be calculated using \(V = l \times w \times h\).

Cylinder

If you have a cylinder with radius = \(r\) and height = \(h\), the volume can be calculated using \(V=\pi \cdot r^2 \cdot h\).

Measuring Surface Area

Because of the number of sides that many solid figures have, calculating surface areas can be a bit more complicated than calculating volumes. Sometimes it helps to visualize the sides by drawing a representation called a net. Imagine taking a cube and cutting three edges of each base and then unfolding the rest to lie flat. Below you can see a couple of ways this could be done. The bases are marked with a B. It’s clear that the cube is made out of six identical squares, which leads to this formula for surface area: \(SA = 6s^2\), where \(s\) is the length of each square’s side.

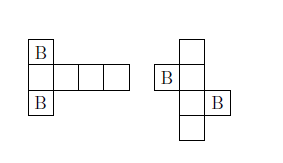
Rectangular Solid

Looking at the figure below carefully, you can perhaps see that there are three different sizes of sides, and there are two sides of each size.

We have the top and bottom with measures \(l \times w\). We have the front and back sides with measures \(h \times w\). We have the left and right sides with measures \(l \times h\). Putting these together, we have the formula for the surface area of a rectangular solid.

\[SA = 2 lw +2 hw +2 lh\]

Cylinder

In a cylinder the top and the bottom are both circles whose areas are each \(\pi r^2\). Picture the side as a rectangle wrapped around the circles. One side of the rectangle has a length \(h\) and the other side will be the circumference of the circles (\(2 \pi r\)).

Putting these together, we have the formula for the surface area of a cylinder.

\[SA = 2\pi r h + 2 \pi r^2 \text{, or, factored, } SA=2\pi r(h+r)\]

Coordinate Geometry

Coordinate geometry provides a way to link algebra and geometry. Through coordinate geometry you can interpret algebraic equations in terms of lines and curves. The next few sections describe the coordinate geometry of straight lines.

The Coordinate Grid

The coordinate grid is a way of using two numbers to describe the location of any point in a plane. It starts with two lines that intersect at a right angle. One line is horizontal, labeled the \(x\)-axis, and the other line is vertical, and is labeled the \(y\)-axis. The point where they intersect is labeled \((0,0)\). All other points in the plane are measured from this point.

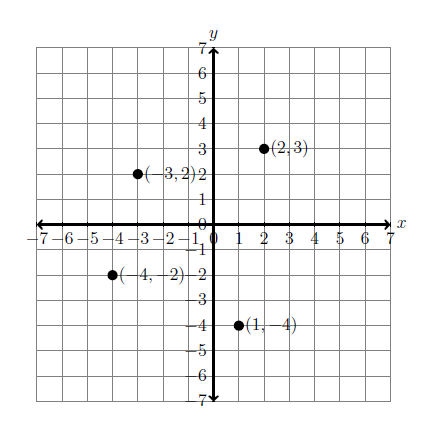
Coordinates

A set of coordinates is a pair of numbers in the form \((x, y)\) that describes the location of a point. The \(x\) tells you how far the point is horizontally from \((0, 0)\), and the \(y\) tells you how far vertically the point is from \((0, 0)\). For example, in the grid above, you can see a point labeled \(2, 3)\). It is located \(2\) places to the right of \((0, 0)\), and \(3\) places up. You can see on the grid that to the left of \((0, 0)\) the \(x\) values are negative, and below \((0, 0)\) the \(y\) values are negative. Check out the other three points to make sure you know how the system works.

\(x-\) and \(y-*\) Intercepts

When a graph intersects the \(x\)-axis or the \(y\)-axis, the points of intersection with the axes are called the \(x\)-intercept and the \(y\)-intercept, respectively. In the figure below, the \(x\)-intercept is \((2, 0)\) and the \(y\)-intercept is \((0, -2)\).

Slope

The slope of a line graph is what it sounds like: a measure of the steepness of the line. The steeper the line, the higher the slope. (Slopes can be negative, so technically, we should say the higher the absolute value of the slope, the steeper it is.)

A horizontal line has a slope of zero, and a vertical line’s slope is undefined. A line that rises from left to right has a positive slope, whereas a line that goes downhill from left to right has a negative slope.

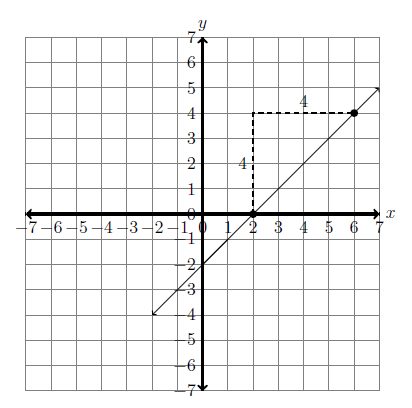
Finding Slope

To calculate the slope of a line, pick any two points on the line and use the formula below. Think of one point as \((x_1, y_1)\) and the second point as \((x_2, y_2)\). The letter \(m\) represents the slope.

\[m = \dfrac{y_2-y_1}{x_2-x_1}\]

Using the figure above, we will pick two points on the graph. \((2, 0)\) and \((6, 4)\). It doesn’t matter which point you think of as \((x_1, y_1)\), but just to help you be consistent, it may help to always think of the first point mentioned as \((x_1, y_1)\).

Calculating slope:

\[m = \dfrac{4-0}{6-2}\] \[m = \dfrac{4}{4} = 1\]

To help remember which number goes on top in the slope formula, a tried and true method is to remember that slope equals rise over run. The rise will be negative if the line goes downhill from left to right. The run is always positive.

Slope-Intercept Form

Equations for straight lines can be in different forms. One that is commonly used is called the slope-intercept form. It looks like this: \(y=mx+b\).

The slope of the line is \(m\) and the \(y\)-intercept is the point \((0,b)\).

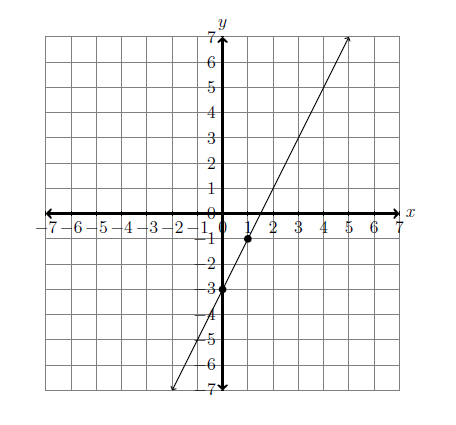
This form makes it fairly easy to quickly sketch a linear graph. For example, consider \(y=2x-3\). The graph will have a slope of \(2\) and will pass through the point \((0, -3)\).

To sketch the graph, place one point at \((0, -3)\). From there, place the second point up \(2\) places and to the right \(1\) place. The second point will be \((1, -1)\). Draw a line through the two points. It should look like the figure below.

Finding Distance

Just as with the slope formula, we will use \((x_1, y_1)\) and \((x_2, y_2)\) to represent two points.

The Distance Formula

To find the distance between two points, we can use the distance formula:

\[d=\sqrt{(x_2-x_1)^2 +(y_2-y_1)^2}\]

As an example, let’s find the distance between the points \((-6, 2)\) and \((6,-3)\).

\[d=\sqrt{(6-(-6))^2 +(-3-2)^2}\] \[d=\sqrt{(12)^2 +(-5)^2}\] \[d=\sqrt{144+25}\] \[d = 13\]

The Midpoint Formula

If there is a segment joining the points \((x_1, y_1)\) and \((x_2, y_2)\), we can use this formula to calculate the midpoint of that segment:

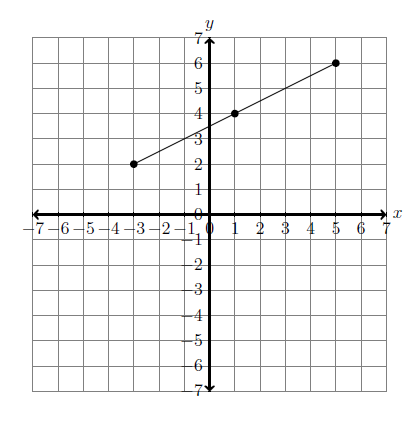
\[m.p. = \left(\dfrac{(x_1+x_2)}{2} , \dfrac{(y_1+y_2)}{2}\right)\]

As an example, we can calculate the midpoint of the segment from \((-3, 2)\) to \((5, 6)\):

\[m.p. = \left(\dfrac{(-3+5)}{2} , \dfrac{(2+6)}{2}\right)\] \[m.p. = \left(\dfrac{2}{2} , \dfrac{8}{2}\right)\] \[m.p. = (1, 4)\]

This figure shows the three points.