Mathematics Knowledge Study Guide for the ASVAB

Geometry: Part 2

Polygons

A polygon is a closed geometric shape bounded by line segments. Common polygons are listed below.

\[\begin{array}{cc} \text{Number of Sides} & \text{Name}\\ \hline 3 & \text{Triangle}\\ 4 & \text{Quadrilateral}\\ 5 & \text{Pentagon}\\ 6 & \text{Hexagon}\\ 7 & \text{Heptagon}\\ 8 & \text{Octagon}\\ 9 & \text{Nonagon}\\ 10 & \text{Decagon}\\ \end{array}\]

Regular Polygons

Regular polygons have all sides congruent and all angles congruent. Another way to say this is to say that regular polygons are equilateral and equiangular.

Exterior and Interior Angles

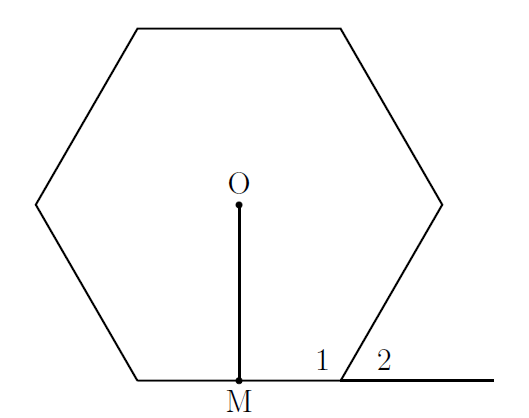
An interior angle of a polygon is the angle formed by the intersection of two sides. In the hexagon below, \(\angle 1\) is an interior angle. An exterior angle is formed by extending one side past a vertex. \(\angle 2\) is an exterior angle.

Finding the Sum of Interior Angles

The sum of interior angles in a polygon is found by using\(S = (n-2) \cdot 180^\circ\), where \(n\) is the number of sides in the polygon. For example, the sum of interior angles in a hexagon is \((6-2) \cdot 180^\circ = 720^\circ\).

Finding the Measure of a Single Angle

If the polygon is regular, you can find the measure of an interior angle by dividing the sum of angles by the number of sides. For example, in a hexagon, we can divide the sum \(720^\circ\) by \(6\) and get \(120^\circ\) for each interior angle.

Apothem

An apothem is a segment drawn from the center of a regular polygon to the midpoint of one of the sides. \(\overline{OM}\) is an apothem.

Triangles

A triangle is a closed figure bounded by three line segments.

Important Parts of Triangles

All of these, with the probable exception of centroid and orthocenter, are commonly used terms and are worth knowing.

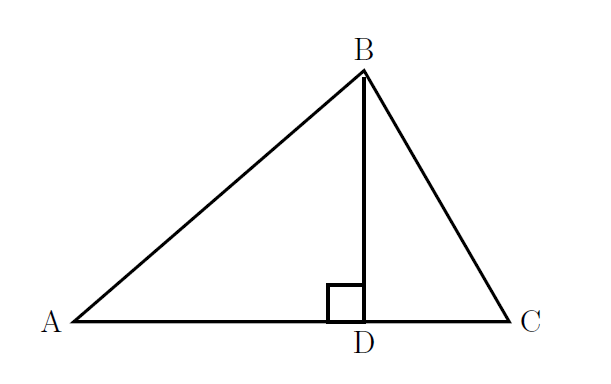
Altitude—The altitude (also known as the height) of a triangle is a segment drawn from a vertex and perpendicular to the opposite side. \(\overline{BD}\) is an altitude.

Base—The base is generally thought of as the bottom side of a triangle, though the triangle can be rotated to make any of the three sides the base. In the following triangle, \(\overline{CB}\) would be most likely thought of as the base.

Base Angles—The angles on either end of the base are known as base angles. In the triangle above, \(\angle C\) and \(\angle B\) would be base angles.

Vertex—A vertex is a point where the sides of a triangle intersect. The plural of vertex is vertices and triangles have three of them.

Angle bisector—As mentioned and shown previously, an angle bisector divides an angle into two congruent angles.

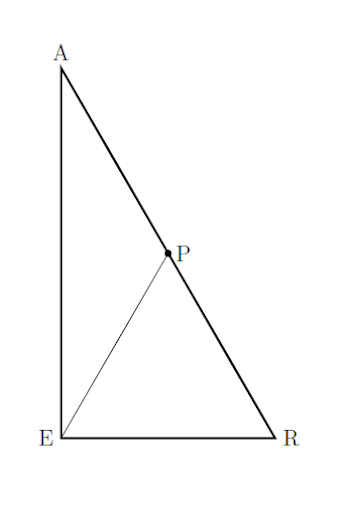
Median—A segment drawn from a vertex to the midpoint of the opposite side is a median. In this figure, P is the midpoint of \(\overline{AR}\) and \(\overline{EP}\) is a median.

Centroid—If you draw all three medians in a triangle, they will intersect at one point. That point is called the centroid. Point D is the centroid in the triangle below.

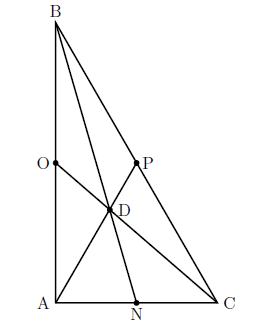
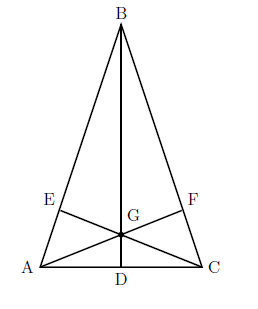
Orthocenter—If you draw three altitudes in a triangle, they will intersect in one point. That point is called the orthocenter. G is the orthocenter in the triangle below.

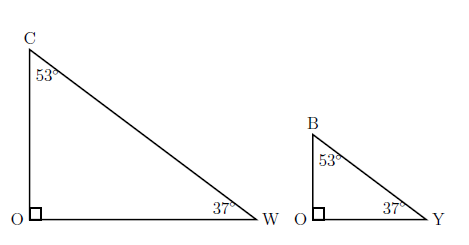
Similar Triangles

Similar triangles have the same shape, but not necessarily the same size. A more mathematical way to say it is in similar triangles, corresponding sides all have the same ratio. \(\triangle{COW}\) is similar to \(\triangle{BOY}\). Symbolically, \(\triangle{COW} \sim \triangle{BOY}\).

Types of Triangles

Triangles are classified in terms of their side lengths and their angles.

Isosceles—If a triangle has two congruent sides, it is an isosceles triangle. In this triangle, \(\overline{CO} \cong \overline{OB}\), so \(\triangle{COB}\) is isosceles.

Equilateral—If a triangle has all three sides congruent, it is an equilateral triangle. \(\triangle EAR\) is an equilateral triangle.

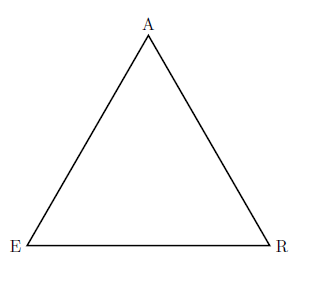
Scalene—Scalene triangles have no two sides congruent.

Acute—Acute triangles have three acute angles. The equilateral triangle shown earlier is one.

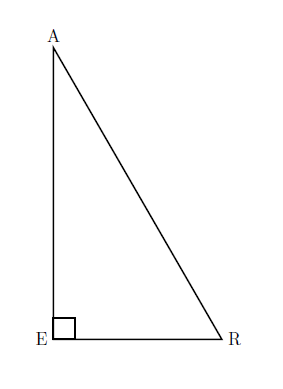
Right— A triangle that contains a right angle is a right triangle. \(\triangle ARE\) is a right triangle. (It’s also a scalene triangle.)

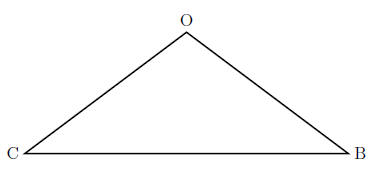
Obtuse—Obtuse triangles have one obtuse triangle, like \(\triangle COB\) below. (It’s also an isosceles triangle, as we saw before.)

The Triangle Inequality Theorem

The sum of any two sides in a triangle must be greater than the third side. For example, if two sides of a triangle are \(4\) and \(6\), the third side must be less than \(10\).

The Third Side Rule

If you choose any two sides of a triangle, the third side must be between their sum and their difference. For example, if a triangle has \(6\) and \(2\) for sides, the third side must be between \(6-2\) and \(6+2\) (i.e., the third side must be between \(4\) and \(8\)).

The Pythagorean Theorem

This is one of the most well-known theorems in geometry. In any right triangle, the sum of the squares of the legs is equal to the square of the hypotenuse. In terms of the drawing below, that means \(a^2 + b^2 = c^2\).

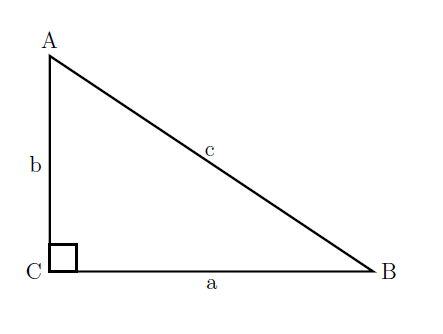
For example, if \(a=6\) and \(b=4\), how long is \(c\)?

\[6^2+4^2=c^2\] \[36+16=c^2\] \[52=c^2\] \[c= \sqrt{52}\] \[c = \sqrt{4 \cdot 13}\] \[c=2\sqrt{13}\]

Assessing and Measuring Combined Figures

Sometimes on a geometry test, you will be called on to calculate some aspects of a figure in which two or more geometric shapes have been combined. Here is an easy example. Given that \(LUCH\) is a square with \(\overline{LU} = 10\), and \(\triangle UNC\) is equilateral, what is the perimeter of figure LUNCH?

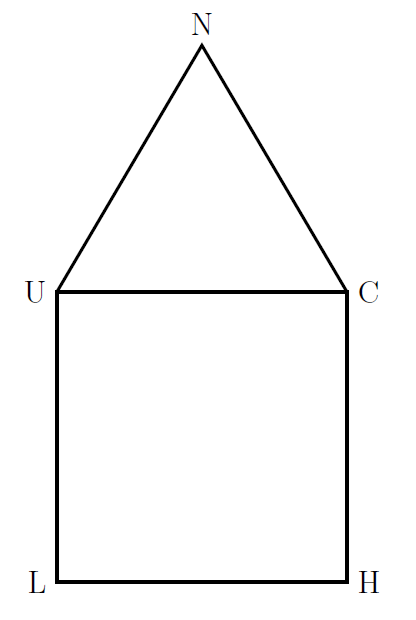
Given that figure LUCH is a square with sides of \(10\), and \(\triangle UNC\) is equilateral, we can deduce that all sides of the figure have lengths of \(10\). The figure LUNCH has five sides, which makes the perimeter \(50\).

Quadrilaterals

A figure with four sides is a quadrilateral. Special ones worth knowing are listed below.

Parallelogram—A parallelogram is a quadrilateral with both pairs of opposite sides parallel.

Rectangle—A rectangle is a parallelogram with a right angle. (Rectangles will actually have four right angles, but it’s sufficient to say one right angle in the definition.)

Rhombus—A rhombus is a parallelogram with four congruent sides.

Square—A square is a rectangle that is also a rhombus.

Trapezoid—A trapezoid is a quadrilateral with only one pair of parallel sides.

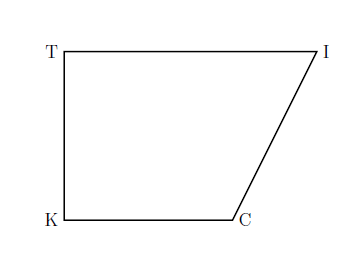
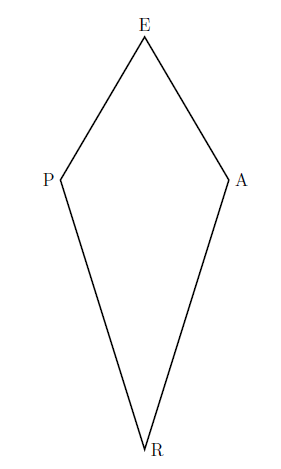
Kite—A kite is a quadrilateral with two distinct pairs of congruent adjacent sides.

Circles

A circle is a set of points a given distance from a given point.

Parts of a Circle

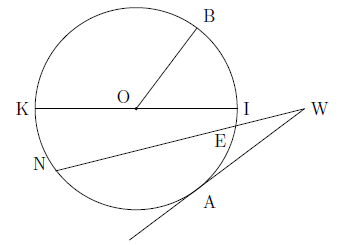
Center—A circle is a set of points a given distance from a given point. The given point is the center of the circle, point O in the figure above, and is equidistant from all points on the circle.

Radius—A circle is a set of points a given distance from a given point, or the center of the circle. The given distance is the radius of the circle, \(\overline{OB}\) in the figure.

Diameter—The diameter is a line segment through the center of a circle whose endpoints lie on the circle, \(\overline{KI}\) in the figure.

Chord—A chord is a line segment whose endpoints lie on the circle. Both \(\overline{KI}\) and \(\overline{NE}\) in the figure are chords.

Secant—A secant is a line that intersects a circle in two points, \(\overline{NW}\) in the figure.

Tangent—A tangent is a line that intersects a circle in only one point, \(\overline{WA}\) in the figure.

Measuring a Circle

Like any other geometric shape, circles have an area and a perimeter. Sometimes just a portion of the circumference is needed. That would be an arc.

Circumference—The circumference is the distance around a circle. Think of it as the perimeter of the circle. You can calculate it by using \(C=\pi \cdot d\).

Area—The area of a circle is the space contained within it. The area of a circle can be calculated using the formula \(A = \pi \cdot r^2\).

Angles in a Circle

It’s possible to draw lines or segments that intersect with the circle in different ways. The angles that are formed are described below.

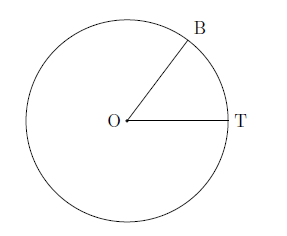
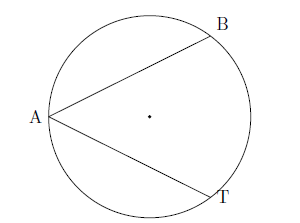
Central angle—An angle that has its vertex on the center of the circle and endpoints on the circle is a central angle. The sides of the angle intercept an arc. \(\angle BOT\) is a central angle. The measure of \(\newcommand{arc}[1]{\stackrel{\Large\frown}{#1}}\arc{BT}\) is the same as the measure of the angle.

Inscribed angle—An inscribed angle has its vertex on the circle and its sides intersect the circle. \(\angle BAT\) is an inscribed angle. The measure of \(\angle BAT\) is half the intercepted arc \(\newcommand{arc}[1]{\stackrel{\Large\frown}{#1}}\arc{BT}\).

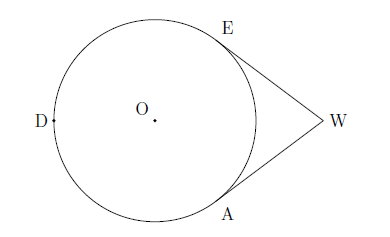
Circumscribed angle— A circumscribed angle is one formed by two tangents to a circle. If \(\overline{WE}\) and \(\overline{WA}\) are tangents to circle \(O\), then \(\angle{AWE}\) is a circumscribed angle. The measure of \(\angle{AWE}\) is half the difference between the arcs \(\overset{\mmlToken{mo}{⏜}}{ADE\,}\) and \(\newcommand{arc}[1]{\stackrel{\Large\frown}{#1}}\arc{EA}\).

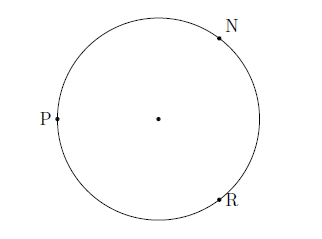
Arc—An arc is a portion of a circle. If it is less than \(180^\circ\), it is a minor arc. A major arc is greater than \(180^\circ\). In this circle, the arc \(\newcommand{arc}[1]{\stackrel{\Large\frown}{#1}}\arc{NR}\) on the right is a minor arc. On the left, \(\overset{\mmlToken{mo}{⏜}}{NPR\,}\) is a major arc.

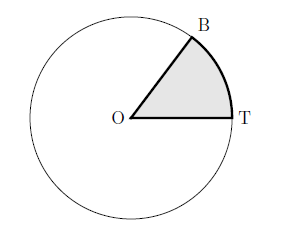
Sector—A sector is a pie-shaped piece of a circle. In this figure, the shaded area bounded by \(\overline{OT}\), \(\overline{OB}\), and the arc \(\newcommand{arc}[1]{\stackrel{\Large\frown}{#1}}\arc{BT}\) is a sector.