Mathematics Study Guide for the ACT

Algebra: Part 2

Inequalities

Inequalities are mathematical expressions that compare two values or expressions and indicate which value is greater than, less than, or equal to the other. These are the inequality symbols:

Linear inequalities are inequalities in which the highest power of the variable is one, while compound inequalities are inequalities that contain more than one inequality symbol.

Solving Inequalities

Solving inequalities is quite similar to solving equations, with one major difference. When we multiply or divide both sides of an inequality by a negative number, we need to reverse the inequality symbol.

Let’s solve the linear inequality \(-3x + 10 \geq 7\).

First, we subtract \(10\) from both sides to isolate the term with \(x\):

\[-3x + 10 - 10 \geq 7 - 10\] \[-3x \geq -3\]

To solve for \(x\), we divide both sides by \(-3\) and remember to reverse the inequality sign:

\[\frac{-3x}{-3} \leq \frac{-3}{-3}\] \[x \leq 1\]

Here is an example of a compound inequality:

\[2x + 2 < x < 3x - 2\]

The way to solve this is to separate the compound inequality into two parts:

\[2x + 2 < x \,\text{ and }\, x < 3x - 2\]

Then we solve each part and write both solution sets together.

This is what the complete solution looks like:

\[\begin{array}{r} & 2x+2 < x & \quad \quad x<3x -2 \\ & 2x < x -2 & \quad \quad x - 3x < -2 \\ & x < -1 & \quad \quad -2x < -2 \\ & & \quad \quad 2x > 2 \\ & & \quad \quad x > 1 \\ \end{array}\]

Result: \(x<-1 \text{ or } x > 1\)

Matching Inequalities to Graphs on Number Line

Once we solve an inequality, either linear or compound, we can graph it on a number line. For linear inequalities, we can have the following types of solutions:

\[x < a \,\text{ or }\, x > a\]

For compound inequalities, we can have the following types of solutions:

\[a < x < b\,\text{ or }\, x < b\,\text{ and }\,x >a\]

Using the figure below, you can match the different types of inequalities on a number line:

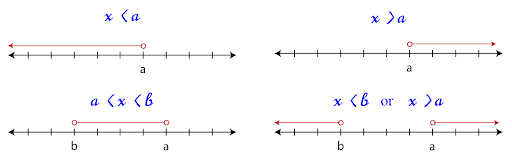
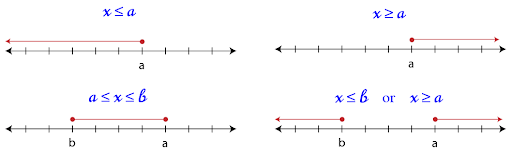
Note that at \(a\), the circle is an open circle because the inequality symbol is either \(<\) or \(>\). If it were \(\leq\) or \(\geq\), the circle would be a closed circle, as shown below:

Quadratic Equations

A quadratic equation is a second-degree equation with one variable. The highest power of the variable is \(\boldsymbol{2}\). The general form of a quadratic equation is \(ax^2 + bx + c = 0\), where \(a\), \(b\), and \(c\) are constants and \(x\) is the variable. Note that both \(b\) and \(c\) can be \(0\), but \(a\) cannot be equal to \(0\).

Solving

Solving quadratic equations means finding the roots (solutions). There can be zero, one, or two real roots for quadratics. There are four main methods for solving a quadratic: factoring, completing the square, the quadratic formula, and graphing.

Factoring

When we solve a quadratic equation by factoring, we express it as two factors being multiplied to give the quadratic equation. To factor a quadratic of the form \(ax^2 + bx + c = 0\), you need to find two numbers, say \(j\) and \(k\), whose product is equal to \(a \times c\) and whose sum is equal to \(b\). Once you find \(j\) and \(k\), you can write the quadratic equation in the form \((x+j)(x+k)\). Then, you can solve for the values of \(x\) by setting each factor equal to \(0\) and solving for \(x\).

Completing the Square

The completing the square method involves converting the quadratic equation into a perfect square trinomial, \(ax^2 + bx + c\), which can easily be factored. To complete the square for the equation \(ax^2 + bx + c = 0\), follow these steps:

1. Subtract \(c\) from both sides.

2. Calculate \(\left(\frac{b}{2a}\right)^{2}\) and add it to both sides. The left side will now be a perfect square.

3. Take the square root of both sides and solve the equation.

The Quadratic Formula

Using the quadratic formula, you can solve any quadratic equation in the form \(ax^2 +bx + c = 0\). The quadratic formula is:

\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]

where \(a\) is the coefficient of \(x^2\), \(b\) is the coefficient of \(x\), and \(c\) is the constant term.

This method for solving a quadratic equation works for all quadratic equations, regardless of whether they can be factored or not. You can find complex solutions as well.

Graphing

To solve a quadratic equation by graphing, we graph the parabola (this is the shape of a quadratic equation) and find its \(x\)-intercepts (\(x\)-axis cutting point) by either estimating from the graph or finding the exact value. The \(x\)-intercepts are the solutions of the quadratic equation. Graphing is not the most efficient method for finding the solutions of a quadratic equation, but it can be useful for visualizing the problem and understanding its properties. It is also a good method for checking the accuracy of the solutions obtained by other methods.

Matching Quadratic Equations with Their Graphs

To match quadratic equations with their graphs, we need to review several key points:

• Look at the coefficient of \(x^2\). If it is positive, the parabola opens upward and the vertex is at the lowest point. If it is negative, the parabola opens downward and the vertex is at the highest point.

• Find the vertex coordinates using the formula \(\left(-\frac{b}{2a}, \frac{4ac-b^2}{4a}\right)\).

• Identify the axis of symmetry. This is the vertical line going through the vertex.

• Find the \(x\)-intercepts by solving the quadratic equation. Set \(y=0\) and solve for the values of \(x\).

• Draw the parabola.

By following these guidelines, we can visually understand the behavior of quadratic equations and accurately match them with their graphs.

Exponential Equations

In exponential equations, one or more variables appear as exponents (powers). Compound interest, population growth models, and radioactive decay equations are all modeled by the general exponential equation:

\[y = ab^{x}\]

where \(a\) and \(b\) are constants, \(x\) is the variable exponent, and \(y\) is the output.

To solve exponential equations, we use logarithms (or natural logarithms) to isolate the variable exponent. We use logarithm laws to simplify the expression and solve for the unknown. Logarithms allow us to convert an exponential equation into a linear equation.

Radical Equations

An equation that contains one or more roots is called a radical equation. The roots are usually square and cube roots. For example, \(\sqrt{x+2} = 9\) is a radical equation. They are usually harder to solve than linear or quadratic equations. To solve radical equations, we use the radical isolation process. It involves isolating the radical expression to one side of the equation and then squaring both sides to eliminate the radical. The resulting equation is then solved using algebraic techniques.

Systems of Equations

A system of equations is a set of two or more equations with two or more variables. The solution to the system is the set of values for the variables that satisfy all of the equations. For example, below we show a system of two equations with two variables (\(x\) and \(y\)):

\[\begin{cases} 2x + 3y = 10 \\ x - y = 5 \end{cases}\]

There are three main methods for solving a system: substitution, elimination, and graphing.

The substitution method involves solving one equation for one of the variables and then substituting that expression into the other equation. This way, we have an equation with one variable that can be solved. Lastly, we use the value of one of the variables and substitute it back into any of the original equations and solve for the other variable.

The elimination method involves adding or subtracting the equation in a system to eliminate one of the variables. If required, before adding/subtracting, you have to multiply one or both equations in the system to make it such that one of the variables is eliminated. Now, you can solve for the value of one variable. Then, we solve for the remaining variable by substituting this value back into either one of the original equations.

The graphing method involves graphing each linear equation on the coordinate plane and observing the intersection point. The point of intersection represents the solution to the system of equations.

Absolute Value Equations

Absolute value equations involve the absolute value of a variable. Recall that the absolute value of a number is the distance between that number and zero on a number line. Usually, absolute value equations have two solutions since the distance between a number and zero is the same as the distance between the opposite of the number and zero.

Below, we show two absolute value equations:

\[\vert 3x - 3 \vert = 9\] \[\vert 2x \vert -4 = 12\]

Here are the steps to solve an absolute value equation:

1. Isolate the term with the absolute value to one side.

2. Write two separate equations. One of them should be using the positive value of the absolute value term, and the other using the negative value of the absolute value term.

3. Solve each equation from step \(\#2\) separately.

4. Check both solutions by plugging them back into the original equation.