Mathematics Study Guide for the ACT

Number and Quantity: Part 2

Factoring and Multiples

A factor is a number that divides a given number exactly without leaving any remainder. For example, the factors of \(6\) are \(1, \, 2, \, 3,\) and \(6\).

Multiples are numbers that can be obtained by multiplying a given number by any integer. To find the multiples of \(4\), we multiply \(4\) by the integers \(1, \, 2, \, 3, \, 4,\) etc. So, the first four multiples of \(4\) are \(4, \, 8, \, 12,\) and \(16\). There are infinite multiples of any given number.

Prime Numbers

A prime number is a number that can only be expressed as a product of \(1\) and itself, meaning it does not have any factors other than \(\boldsymbol{1}\) and the number itself. The only even prime number is \(\boldsymbol{2}\). It is also the first prime number.

All numbers that are not prime are known as composite numbers. They are numbers that have more than two factors.

Greatest Common Factor (GCF)

The GCF of two numbers is the largest of all factors that two numbers share. For example, the GCF of \(4\) and \(6\) is \(2\) because that is the largest factor that goes into both numbers.

Least Common Multiple (LCM)

The LCM of two numbers is the lowest of the multiples the two numbers have in common. For example, the LCM of \(4\) and \(6\) is \(12\).

Fractions

Fractions are parts of a whole. The top number is called the numerator, and the bottom number is called the denominator. There are three types of fractions: proper fractions, improper fractions, and mixed fractions.

Proper fractions are fractions in which the numerator is less than the denominator. For example, \(\frac{2}{3}\) and \(\frac{1}{4}\) are proper fractions.

Improper fractions are fractions in which the numerator is greater than the denominator. For example, \(\frac{11}{3}\) and \(\frac{7}{5}\) are improper fractions.

Mixed fractions, also known as mixed numbers, are a combination of a whole number and a proper fraction. For example, \(3 \frac{1}{4}\) is a mixed fraction where \(3\) is the whole part and \(\frac{1}{4}\) is the fractional part.

Reducing Fractions to Lowest Terms

Reducing fractions to their lowest terms means reducing the fraction so that both the numerator and the denominator have no common factors other than \(1\). This is achieved by dividing both the top and bottom of a fraction by their GCF. This process ensures that the fraction cannot be simplified any further.

Equivalent Fractions

When two fractions have different numerators and denominators but have the same value, they are equivalent fractions. For instance, \(\frac{1}{2}\) and \(\frac{2}{4}\) are equivalent.

Ordering Fractions

Ordering fractions means arranging them in ascending or descending order based on their values. To order fractions, you can either convert them to decimals and compare them or find a common denominator and compare their numerators.

Adding, Subtracting, Multiplying and Dividing Fractions

To add or subtract fractions, you need to have a common denominator. Then you can add or subtract the numerators and simplify the fraction if necessary.

To multiply fractions, you multiply the numerators together and multiply the denominators together, and then you can simplify the resulting fraction if necessary.

In division, we divide one number by another to get a result. The number being divided is called the dividend, the number doing the dividing is called the divisor, and the result is the quotient. To divide fractions, you need to invert the second fraction (divisor) and then multiply the two fractions. This process is sometimes called “inverting and multiplying.”

Using the Number Line

The number line shows the location of numbers on a straight line that extends infinitely in both directions and is marked with regularly spaced tick marks. It is a pictorial representation of numbers and their relationship to each other. The tick marks on the number line represent numbers, and the distance between them is usually uniform. A typical number line is shown below:

Absolute Value

Absolute value is the mathematical function that tells us the distance of a number from \(\boldsymbol{0}\). Since absolute value is a distance, it is always positive, even if the number is negative. To find the absolute value of a negative number, we simply remove the negative sign. So, the absolute value of both \(3\) and \(-3\) is \(3\).

Exponents

Exponents are shorthand notations of repeated multiplication. They are used to express large or small numbers in compact form. There is a base number and a small number written to the top-right of the base number, which is the exponent:

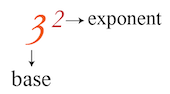
The above figure shows \(3\) as the base number and \(2\) as the exponent. It tells us to multiply two \(3\)s by each other. So, \(3^{2} = 3 \times 3 = 9\).

Squares and Cubes

Squares and cubes are exponents that involve raising a number to the second or third power, respectively. Squaring a number means to multiply two of that number together and cubing means to multiply three of that number together. For example, the square of \(5\) is \(25\):

\[5^{2} = 5 \times 5 = 25\]

The cube of \(5\) is \(125\):

\[5^{3} = 5 \times 5 \times 5 = 125\]

Square and Cube Roots

Square roots and cube roots are the inverse operations of squaring and cubing a number. They are used to find the number that, when squared or cubed, equals a given number. For example, the square root of \(25\) is \(5\) since \(5^{2} = 25\):

\[\sqrt{25} = 5 \,\text{ and }\, 5^2 = 25\]

Also, the cube root of \(27\) is \(3\) since \(3^{3} = 27\):

\(\sqrt[3]{27} = 3 \,\text{ and }\,\)3^{3} = 27 $$

Powers of Ten

The term powers of ten refers to the exponents of the number \(10\). They are used to represent very large or very small numbers in a convenient way. For example, the number \(10\text{,}000\) can be written with a power of ten:

\[10^4 = 10\text{,}000\]

The number \(0.0001\) can be written as:

\[10^{-4} = 0.0001\]

Properties of Rational Exponents

Rational exponents are powers that are expressed as fractions. They are written in the form \(a^{\frac{m}{n}}\), where \(a\) is the base and \(\frac{m}{n}\) is the fractional power. The laws of exponents hold true for rational exponents as well. If \(x\) and \(y\) are fractions, then the rules of rational exponents are:

\[a^{x} \times a^{y} = a^{x+y}\] \[a^{x} \div a^{y} = a^{x-y}\] \[(a^x)^{y} = a^{xy}\] \[a^{-x} = \frac{1}{a^x}\]

Scientific Notation

Using scientific notation, we can write very large and small numbers in a compact way. It’s done by writing a number as a product of a coefficient and a power of ten. It uses this form:

\[a \times 10^{b}\]

The coefficient, \(a\), is a number between \(1\) and \(10\), and the power of ten, \(b\), tells you how many places to move the decimal point. To convert a number written in scientific notation, you can follow the steps below:

1. Count the places as you move the decimal point to get a coefficient number between \(1\) and \(10\).

2. The number of places you moved the decimal point is the power of ten. If you moved the decimal point to the right, the power of ten is negative. If you moved the decimal point to the left, the power of ten is positive.

3. Write the number as the coefficient times \(10\) raised to the power you found in step \(\#2\).

We’ll look at an example.

The distance to the sun is \(93\text{,}000\text{,}000\) miles. Write this in scientific notation.

Starting at the extreme right end, move the decimal point leftward until only the nine is to its left, giving us \(9.3\). Notice that the decimal point moved seven places. Seven will be the exponent: \(10^7\). Put the two numbers together, and you will have \(9.3 \times 10^7\) miles.

Matrices

A matrix is a rectangular array representation of numbers, variables, or both. It has rows and columns. The order of a matrix is the size of the matrix. If a matrix has \(m\) rows and \(n\) columns, the order of the matrix is \(m \times n\). It is read as an “m by n” matrix. Each individual entry of the matrix is known as an element. We can name a matrix using capital letters, such as A, B, C, etc. Below, we show two sample matrices, matrix \(A\) and matrix \(B\):

Matrix \(A\) is a \(2 \times 2\) matrix and matrix \(B\) is a \(2 \times 3\) matrix.

On the ACT you may be asked to do three operations with matrices: addition, subtraction, and scalar multiplication.

Vectors

Vectors are quantities that have both a magnitude and direction. They are used to represent physical quantities such as force, velocity, displacement, etc. There are several ways to denote vectors. The simplest is to write the vector as Cartesian coordinates.

For example, let’s say we have the vector \(B = (2,5)\). In column vector format, we can write it as \(B = \begin{pmatrix} 2 \\ 5 \end{pmatrix}\). Using unit vector notation, you can write it as \(B = 2i + 5j\), where \(i\) and \(j\) are unit vectors (vectors with length \(1\)) in the \(x\) and \(y\) directions, respectively.

Vectors can be represented graphically with arrows. Consider the vector \(A\) shown below:

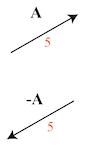
It has a magnitude (length) of \(5\) units and the way the arrow is pointing is its direction. If you keep the length the same but flip it to the opposite direction, you have the vector \(-A\).

Complex Numbers

A complex number is a number that can be expressed in the form \(a+bi\), where \(a\) and \(b\) are real numbers and \(i\) is the imaginary number equal to \(\sqrt{-1}\). In mathematics, physics, and engineering, there are some problems that cannot be solved using the real number system. The following figure shows the number system:

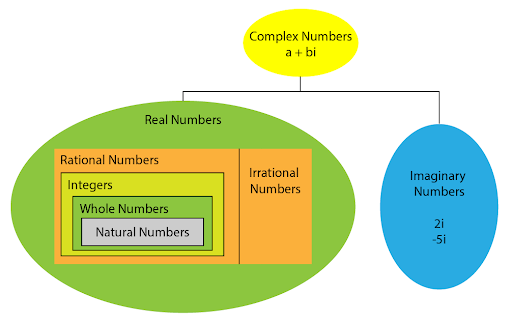
The a is the real part, and the bi is the imaginary part. Complex numbers extend the set of real numbers by including the square root of negative numbers, which is not possible with real numbers alone. When the real part is absent, we call the number an imaginary number. Imaginary numbers form a subset of complex numbers.

Irrational Numbers

Irrational numbers are real numbers that cannot be expressed as a ratio of two integers. The decimal expansion of an irrational number is non-repeating and infinite. Some common irrational numbers are \(\pi\), \(\sqrt{2}\), \(\sqrt{3}\), and \(e\).

The number \(\pi\) is the ratio of a circle’s circumference to its diameter (it is expressed as \(3.14159…\), with an infinite number of numbers after the decimal). The square roots of all prime numbers are also irrational. For the ACT exam, you should have a basic understanding of irrational numbers and their properties. You might be asked to identify the irrational numbers from a set of numbers.

Roots of Real Numbers

A root is the opposite of a power, where a power is a number raised to a certain exponent. A root is the number that, when raised to that exponent, equals the original number. If you raise a number to the \(n^{\text{th}}\) power, taking the \(n^{\text{th}}\) root of that will give you the original number, and vice versa. For example, the square root of \(16\) is \(4\) since \(4^2 = 16\).

On the ACT exam, you will mostly see square roots and cube roots. A number’s square root is the value that we can multiply by itself to obtain that number. To obtain a given number, the cube root is the value that, if taken three times and multiplied, will give us that number.

Note: The square root of a negative number cannot be a real number. This is because no real number can be multiplied by itself to get a negative number.

Sums of Radicals

The key to adding or subtracting radicals is to find the number under the root symbol. If this number is the same, then we can treat radicals as variables and add/subtract just like in algebra. For example, we can add \(\sqrt{2}\) and \(\sqrt{2}\) but we cannot add \(\sqrt{2}\) and \(\sqrt{3}\).