Next Generation Advanced Algebra and Functions Study Guide for the ACCUPLACER Test
Page 6
Radical and Rational Equations
A radical equation is any equation that includes an \(n^{th}\) root: \(\sqrt{x + 2} = 5\), for example.
A rational equation is any equation that includes a polynomial expression in the numerator and/or the denominator: \(\frac{x + 2}{3} + \frac{x - 1}{x + 3} = \frac{x^2}{x - 2}\), for example.
The algebraic techniques necessary to solve either type of equation will be explored below.
Consider the radical equation: \(\sqrt{x - 4} = 3\).
Solving the equation entails isolating \(x\). This is first accomplished by squaring both sides to eliminate the radical:
\((\sqrt{x - 4})^2 = 3^2\), which becomes
\(x - 4 = 9\), and \(x = 13\)
This solution can be verified by substituting the value back into the original equation and simplifying:
\(\sqrt{13 - 4} = \sqrt{9} = 3\).
Even radicals, like the square root function or the fourth root function, do not have real solutions when the value beneath the radical is negative. Odd radicals, like the third and fifth root functions, do have real solutions when the value beneath the radical is negative. Understanding this concept enables the domain and range to be found for functions including radicals.
Consider the rational equation: \(\frac{4}{x + 2} + \frac{3}{x - 2} = 10\)
A useful technique for solving rational equations entails multiplying the entire equation by the expressions in the denominators, doing so yields an equation with terms only in the numerator. In this case, multiply the equation by \((x + 2)(x - 2)\), to give:
\(4x - 8 + 3x + 6 = 10(x^2 - 4)\), which becomes
\(0 = 10x^2 - 7x - 42\).
You can factor the equation as you see fit to solve for \(x\). It is useful to notice that even if you find that \(x = 2\), or \(x = -2\) is a solution to the quadratic, it is not a solution to the original rational equation. If \(x = \pm 2\), substitution of the value into the rational expression produces an undefined expression:
\(\frac{4}{-2 + 2} = \frac{4}{0} =\) undefined.
This is always something to keep in mind when solving rational equations.
Creating
Situations involving a variable raised to a power can occasionally be solved through evaluating the \(n^{th}\) root of the variable. As a result, situations that can be modeled with exponents can be solved by evaluating their roots.
Consider the following example:
The periodic motion of a pendulum is described by an equation that relates the period of the motion, \(T\), to the product of twice pi with the square root of the ratio of the pendulum’s length to the acceleration due to gravity. If the acceleration due to gravity is \(9.8 \frac{m}{s^2}\), and the length of the pendulum is \(5\) meters, what is the period?
To solve, it is first necessary to translate the word problem into its algebraic analog:
\(T = 2\pi \cdot \sqrt{\frac{L}{g}}\). The known values must then be substituted:
\(T = 2\pi \cdot \sqrt{\frac{5}{9.8}}\), and the period can be found:
\(T = 4.49\) seconds
Rational equations involve any case where a variable ends up in the denominator of an expression. Consider this example:
The Lorentz factor, \(\gamma\), is described as the ratio of unity to the square root of the difference between unity and the ratio of velocity, \(v\), squared, to the speed of light, \(c\), squared. Represent the Lorentz factor algebraically, and solve for velocity, \(v\):
\(\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}\) is the Lorentz factor written algebraically.
You can solve for \(v\) and the result should be \(v = c\sqrt{1 - (\frac{1}{\gamma}})^2\)
Finding Domain and Range
The domain of a function is the collection of input, usually \(x\), values for which the function is defined. The range of a function is the collection of possible output, usually \(y\), values for a particular function.
When dealing with radical and rational functions, there are particular cases for which either function is undefined or does not include real values. Consider the following rational function:
\[f(x) = \frac{x + 2}{4x + 5}\]Factor where possible to simplify the process of finding the \(x\) values for which the denominators are undefined. In this case, the denominator is already fully factored:
Set the denominator equal to 0 and solve for \(x\). The values for which the function is undefined can be found:
\(4x + 5 = 0\), which results in \(x = -\frac{5}{4}\).
For the given function, there is a vertical asymptote at \(x = -\frac{5}{4}\). An asymptote is an imaginary line that a function will continuously approach but never touch.
To determine the range, solve the given function for \(x\) and find the values for which \(y\) is undefined. The original function:
\(y = \frac{x + 2}{4x + 5}\). Solving for \(x\):
\(y(4x + 5) = x + 2\), distribute the \(y\):
\(4xy + 5y = x + 2\), rearrange:
\(4xy - x = -5y + 2\), factor out an \(x\) from the left hand side and divide both sides:
\(x = \frac{-5y + 2}{4y - 1}\), set the denominator equal to 0 and solve for \(y\):
\(4y - 1 = 0\) so \(y = \frac{1}{4}\).
The function is not defined at \(y = \frac{1}{4}\), so the range includes all values except for \(y = \frac{1}{4}\), which represents a horizontal asymptote.
The graph of the function is provided here:

Notice that the function gradually curves closer and closer to both the horizontal and vertical asymptote, but touches neither.
A similar method is employed for finding the domain and range of a radical function. Consider the following example:
\[y = \frac{1}{\sqrt{x + 4}}\]With rational equations, we learned that a function is undefined in the case where the denominator is equal to \(0\). With radical equations, a function is also undefined when the value inside the radical is negative (when the function is even, but not odd).
In this case, because there is both a fraction and a radical, set the denominator equal to \(0\) to find the vertical asymptote, and also set the expression inside of the square root greater than \(0\) to find the real values for which the function is defined:
\(\sqrt{x + 4} = 0\), so \(x = -4\) is a vertical asymptote. Also:
\(x + 4 > 0\), so \(x > -4\) shows the real values for which the function is defined.
Using the domain and the parent function of \(y = \frac{1}{\sqrt{x + 4}}\), let’s develop some intuition about the function’s range.
The parent function is \(y = \frac{1}{\sqrt{x}}\), which graphs as:
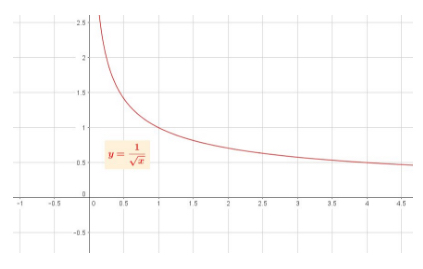
Notice that the parent function can never contain negative values for \(x\) or \(y\). The function exhibits a vertical asymptote at \(x = 0\), and a horizontal asymptote at \(y = 0\).
A comparison between the parent function and the function in question, \(y = \frac{1}{\sqrt{x + 4}}\), shows that our function is only shifted horizontally. This means that only the domain, and not the range, of the parent function is impacted.
Consequently, the range of our function is all values for \(y\) that are greater than \(0\). The graph of the function is provided here:

Graphing
As can be seen from the previous sections, developing familiarity with the general forms of equations, as well as an understanding and intuition of concepts like roots, intercepts, asymptotes, domain, and range greatly facilitates the translation of an algebraic expression to its graphical equivalent.
Recall that any equation can be graphed in a straightforward manner by creating a table of input values and their corresponding output values; however, the process is tedious, and a more efficient method of graphing is desirable.
Rather than taking the tedious table creation approach, it is optimal to utilize familiarity with general function form, and critical points like \(x\) and \(y\) intercepts, as well as presence (or absence) of asymptotes, domain, and range, and end behavior to make easier the translation of an algebraic expression to its corresponding graph.
Let’s graph the following rational equation: \(y = \frac{x^2 - 4}{x^2 + x - 2} - 1\)
The first consideration is always, “Can the equation/expression be simplified via factoring?” In this case, it can:
\[y = \frac{(x + 2)(x - 2)}{(x + 2)(x - 1)} - 1\]Prior to canceling terms that show up in numerator and denominator, it is wise to first establish the domain of the function. Recall that the function is undefined any time there is division by \(0\), so set the fraction portion of the expression equal to \(0\) and solve for \(x\):
\((x + 2)(x - 1) = 0\), so \(x = -2\) and \(x = 1\) are undefined.
Now, because the \(x + 2\) expression can be eliminated (because it is in both numerator and denominator), it exhibits different graphical behavior than \(x - 1\), which acts as a vertical asymptote. Rather than \(x + 2\) acting as an asymptote, it shows up in the graph as an empty circle indicating that the function is not defined at that input value.
The range is a bit more tricky to determine than the domain. In general, when dealing with rational equations, one aspect of the range can be found by comparing the degree of the numerator’s exponent with the degree of the denominator’s exponent to find any horizontal asymptotes. A quick rundown of the different cases:
- If the numerator’s exponent is less than the denominator’s exponent, the horizontal asymptote is \(0\), for example:
- If the numerator’s exponent is equal to the denominator’s exponent, the horizontal asymptote is the ratio of the coefficients, for example:
- An oblique, rather than horizontal asymptote arises when the numerator’s exponent is one degree larger than the denominator’s exponent. In this case, polynomial long division must be used to find the equation of the line of the oblique asymptote. (The remainder is ignored).
- If the numerator’s exponent is more than one degree larger than the denominator’s exponent, there is no horizontal or oblique asymptote:
Returning to our specific example:
\(y = \frac{x^2 - 4}{x^2 + x - 2} - 1\), which can be rewritten as:
\(y = \frac{-x - 2}{x^2 + x - 2}\), and the numerator’s degree is less than the denominator’s degree, so the horizontal asymptote is \(y = 0\).
An additional aspect to consider is the range’s relationship to the domain. In the case where there is a discontinuity, as when a factor containing a variable in the numerator is canceled with itself in the denominator (like \(\frac{x+2}{x+2}\), which gives a discontinuity at \(x = -2\)), the range may also be undefined at the corresponding output value. Substituting this value into the simplified form of the original equation:
\(f(-2) = y = \frac{-2 - 2}{-2 - 1} - 1 = \frac{-4}{-3} - 1 = \frac{1}{3}\), so the range is also undefined at \(y = \frac{1}{3}\).
To find the \(y\)-intercept, evaluate the function at \(x = 0\):
\(y = \frac{0 - 4}{0 + 0 - 2} - 1 = \frac{-4}{-2} - 1 = 2 - 1 = 1\), so the \(y*\)-intercept is \((0, 1)\).
Summarizing the information we have collected thus far:
- vertical asymptote: \(x = 1\)
- a discontinuity at \((-2, \frac{1}{3})\)
- horizontal asymptote: \(y = 0\)
- \(y\)-intercept: \((0, 1)\)
And visualized:
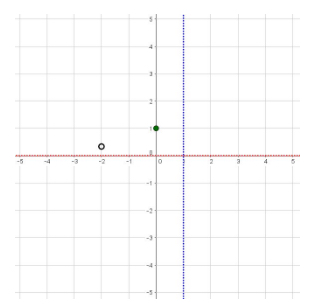
At this point, it is worth inspecting the graph to decide what the likely shape of the function will be. Based on the locations of the y-intercept and the discontinuity, which lie to the left of the vertical asymptote, and above the horizontal asymptote, as well as their relative locations (the discontinuity is below and to the left of the point, it can be deduced that the function will exhibit a general structure of:
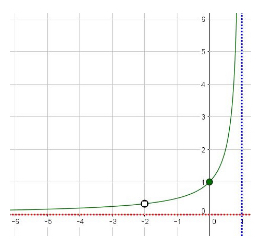
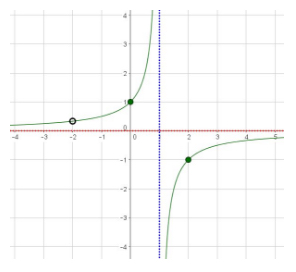
The next step is to determine the behavior of the function to the right of the vertical asymptote. Because we do not have any points guiding us, we must evaluate a value (or values) for \(x\) so that we can determine if the \(y\) values will be above or below the horizontal asymptote. The easiest point to choose is \(2\), as it is the smallest integer value larger than the vertical asymptote value:
\(f(2) = y = \frac{4 - 4}{4 + 2 - 2} - 1 = 0 - 1 = -1\), so the point \((0, -1)\) exists on the curve. Because the \(y\) value is negative, and the horizontal and vertical asymptotes guide the curve’s structure, the right hand side of the function can be graphed:
Now we will practice graphing a radical equation: \(y = \sqrt{x - 2} - 1\)
Recall that radical expressions are undefined when the value beneath the radical is negative (in the case of even valued radicals). So, to determine the values for which the function is undefined, set up an inequality using the expression beneath the radical:
\(x - 2 \ge 0\), which gives \(x \ge 2\), indicating that the function’s real-valued domain includes all \(x\) values greater than or equal to \(2\). Substitute \(x = 2\) into the equation to find the “first” point for which the function is defined:
\(f(2) = y = \sqrt{2 - 2} - 1 = -1\), so the point \((2, -1)\) will serve as the first point on our graph.
Because the radical is presented without a \(\pm\) before it, only the positive values of the function will be graphed. The next step is finding the \(x\)-intercept(s) of the function. This is done by setting \(y = 0\) and solving for \(x\):
\(0 = \sqrt{x - 2} - 1\), which gives
\(x = 3\), so the point \((3, 0)\) is also on the graph. From these two points, and a familiarity with the general form of the radical function, the graph can be produced:
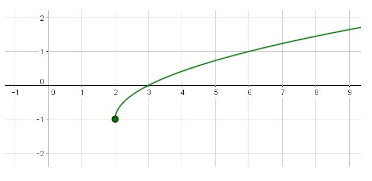
Simplifying
The rules governing exponents are equally applicable to expressions and equations involving radicals. This is because radicals are equivalent to fractional exponents: \(\sqrt{x} = x^\left(\frac{1}{2}\right)\), for example. Consequently, expressions and equations involving the multiplication and division of radicals, as well as the addition and subtraction of radicals of the same type can be simplified.
Consider the following expression:
\[\frac{x^\left(\frac{3}{2}\right)\cdot x^\left(\frac{3}{7}\right)}{x^\left(\frac{2}{3}\right)} + x^\left(\frac{1}{2}\right) - 5x^\left(\frac{1}{2}\right)\]Recall the rules of exponents:
\(x^a \cdot x^b = x^\left(a + b\right)\) and \(\frac{x^a}{x^b} = x^\left(a - b\right)\)
Applying these to the expression given, and combining the numerator terms first:
\[x^\left(\frac{3}{2}\right) \cdot x^\left(\frac{3}{7}\right) = x^\left(\frac{21}{14} + \frac{6}{14}\right) = x^\left(\frac{27}{14}\right)\]And, combining numerator and denominator:
\[x^\left(\frac{27}{14}\right) \div x^\left(\frac{2}{3}\right) = x^\left(\frac{27}{14} - \frac{2}{3}\right) = x^\left(\frac{71}{42} - \frac{28}{42}\right) = x^\left(\frac{43}{42}\right)\]which is what the fraction simplifies to. So now we have:
\[x^\left(\frac{43}{42}\right) + x^\left(\frac{1}{2}\right) - 5x^\left(\frac{1}{2}\right)\]Only the last two terms can be combined through subtraction because they share the same exponent value. So, the simplified form of the original expression becomes:
\[x^\left(\frac{43}{42}\right) - 4x^\left(\frac{1}{2}\right)\]All Study Guides for the ACCUPLACER Test are now available as downloadable PDFs