Next Generation Quantitative Reasoning, Algebra, and Statistics Study Guide for the ACCUPLACER Test
Page 1
General Information
This test is generally given to entering college students who are either majoring in non-STEM-related fields or who have not yet declared a major. All questions are multiple-choice and are fairly evenly divided among these skill areas. Areas listed here in italics may be slightly more emphasized than the others.
- Rational numbers: how to compute with them
- Ratio and proportion reasoning/relationships
- Exponents
- Algebraic expressions
- Linear equations: how to create and apply
- Linear equations: how to graph
- Probability and sets
- Descriptive statistics
- Geometry concepts for Pre-Algebra
In spite of the fact that the questions on this test may require more than one step and some mathematical reasoning, your fluency with math operations is also tested, so be sure accuracy is not a problem. You can check out the study materials we offer for the Accuplacer Next Generation Arithmetic Test for practice in accuracy and fluency.
Note: It would be best to check with your testing center for confirmation, but our information indicates that no handheld calculators are allowed during any Accuplacer tests. Apparently, there are some questions that allow calculator use and, for those questions only, an onscreen calculator will appear.
Rational Numbers
It is important that you understand how to perform all operations with rational numbers in any of their various forms (e.g. decimals, fractions, or whole numbers).
Definition
A rational number is any number that can be written as a fraction in which the denominator is not \(0\). These, for example:
\[5 = \frac{5}{1}\] \[-0.2 = -\frac{1}{5}\] \[13.3 = 13\frac{3}{10}\]Irrational numbers are those with a never-ending sequence of digits to the right of the decimal point; any number that cannot be classified as rational is an irrational number. Two examples of an irrational number are:
\[\sqrt{2}\] \[\pi\]Absolute Value
Absolute value is designated by two vertical bars surrounding an expression, like so:
\[\vert4x + 2\vert\]The absolute value represents the distance between a number or expression and \(0\). Absolute values are always positive (unless it is the absolute value of \(0\), which is neither positive nor negative).
For example:
\[\vert-3\vert = 3\] \[\vert4 - 9\vert = \vert-5\vert = 5\]Ratio and Proportion
Ratios relate parts to parts and parts to wholes. Proportions relate ratios to other ratios.
Definitions and Use
A ratio is a relationship between two values expressed as a fraction. Expressions like for every car there are three trucks and miles per hour both indicate a ratio between two things; the first expression can be written in fractional form as:
\[\frac{1\;\text{car}}{3\;\text{trucks}}\]and the second expression can be written as:
\[\frac{\text{miles}}{\text{hour}}\]The constant rate of change represented by a line shows a practical application of ratios. The slope of a line can be described by the ratio of the change in output variable (commonly \(y\)), to the change in input variable (commonly \(x\)). The slope (commonly \(m\)) is expressed algebraically as:
\(m = \frac{y_2 - y_1}{x_2 - x_1}\), where \((x_1, y_1)\) and \((x_2, y_2)\) represent points along the line.
Proportions can be used in cases where two or more ratios are known to be equivalent. Consider this example:
A bush that is \(4\) feet tall casts a shadow of \(9\) feet. What is the shadow length cast by a tree that is \(35\) feet tall?
Set up a proportion to represent the problem:
\[\frac{4\;\text{ft}}{9\;\text{ft}} = \frac{35\;\text{ft}}{\text{x ft}}\]It is important to notice that the ratios in any proportion must match in arrangement. In the proportion above, the height of each object is placed in the numerator, and the length of each shadow is placed in the denominator. The problem can still be solved if each shadow length is in the numerator and each object height is in the denominator, but the problem cannot be solved if one ratio shows the object’s height in the numerator and the other ratio shows the object’s height in the denominator.
Cross multiplication yields a shadow length of \(78.75\;\text{ft}\).
Proportions are useful for finding the unknown side lengths of similar objects, particularly triangles.
Consider the following example involving similar triangles. Solve for \(x\):
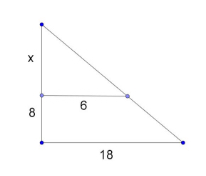
A proportion can be established between the two triangles (as they share two sides):
\[\frac{x}{6} = \frac{x + 8}{18}\]which becomes
\(18x = 6x + 48\), so \(x = 4\)
Determining Rate
A rate expresses the relationship between two quantities of different units. Miles per hour, dollars per minute, and degrees per second are all examples of rates.
Unit rates express a rate in which the denominator is reduced to one. For example, if Sally drives \(200\) miles in \(3.5\) hours, the unit rate describes how many miles she drives in \(1\) hour; stated algebraically, and utilizing a proportion:
\[\frac{200\;\text{miles}}{3.5\;\text{hours}} = \frac{x\;\text{miles}}{1\;\text{hour}}\]which gives:
\[\frac{57.14\;\text{miles}}{1\;\text{hour}}\]Two rates that reduce to the same unit rate are called equivalent rates. Equivalent rates can also be formed by multiplying or dividing both the numerator and denominator of a rate by the same value. A unit rate is always equivalent to the rate from which it was reduced.
Rates can be used to find the total number of one of the units if the other unit of the rate is known. For example, given Sally’s rate of \(\frac{57.14\;\text{miles}}{1\;\text{hour}}\), it can be determined how long it would take her to drive \(450\) miles:
\[450\;\text{miles} \div \frac{57.14\;\text{miles}}{1\;\text{hour}} = 450\;\text{miles} \cdot \frac{1\;\text{hour}}{57.14\;\text{miles}} = 7.88\;\text{hours}\]It can also be determined how many miles she could drive in \(10\) hours:
\[\frac{57.14\;\text{miles}}{1\;\text{hour}} \cdot 10\;\text{hours} = 571.4\;\text{miles}\]Note that when we say, for example, “Sally was driving \(57.14\) miles per hour,” what we are really doing is using a unit rate to talk about her speed. Unit rates make it easy to compare things like speed when distances and the lengths of time traveled differ.
Converting Units
Converting between different units is absolutely crucial for success in the STEM fields. Fortunately, the method of dimensional analysis enables easy assessment of conversion accuracy given that each step of the process eliminates an intermediate unit. An example will prove instructive:
Consider the conversion of \(1.6\) hours to microseconds. Dimensional analysis entails a series of multiplications by conversion factors.
In this case, hours can be converted to minutes (\(1\) hour = \(60\) minutes), and minutes can be converted to seconds (\(1\) minute = \(60\) seconds), and seconds can be converted to microseconds (\(1\) second = \(10^6\) microseconds).
Expressing this conversion algebraically:
\(1.6\;\text{hours} \cdot \frac{60\;\text{minutes}}{1\;\text{hour}} \cdot \frac{60\;\text{seconds}}{1\;\text{minute}} \cdot \frac{10^6\;\text{microseconds}}{1\;\text{second}} = 5.76 \cdot 10^9\) microseconds
Notice that each conversion factor eliminates the previous unit measurement and the final conversion factor yields the desired units. Always ensure that dimensional analysis yields the appropriate units.
All Study Guides for the ACCUPLACER Test are now available as downloadable PDFs