High School Algebra I Study Guide for the STAAR test

Writing and Solving Linear Functions, Equations, and Inequalities

In this section, we will continue to use and build upon what we have reviewed in the last section, Describing and Graphing linear functions. You will find that 14 of the 54 questions on the test will involve these skills.

Writing

Reference will be made to the last section as well as the section on functions when determining how to write linear functions, equations, and inequalities in, or to expedite, the process.

Domain and Range

It is well known that if you exercise more, you will burn more calories. If there is a linear relationship between calories burned and exercise, what are the independent and dependent variables if you were to write a function for this situation?

Since the calories burned are dependent on the amount of exercise you perform, not the other way around, the independent variable is the time you exercise, and the dependent variable is the number of calories you burn.

Next, state the domain and range for the graph of the piece-wise function shown below in interval notation.

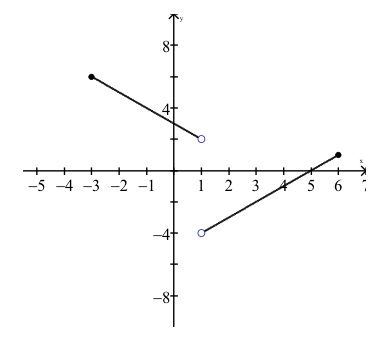
Domain: (-3, 1) and (1, 6) Range: (-4, 1) and (2,6)

Another term you’ll need to know is discrete data. You roll a 6-sided die (a single dice) 12 times to determine how many times you can roll a 3. This is an example of discrete data.

Using Points and Slope

Consider this problem:

Write, in standard form, the equation of a line, if the slope is $-\frac{4}{3}$ and the line contains the point $(2,7)$.

Using the point-slope form we get, $y-7=-\frac{4}{3}(x-2)$. Putting this in standard form, we have:

\[y-7=-\frac{4}{3}(x-2)\] \[y-7=-\frac{4}{3}x+\frac{8}{3}\] \[\frac{4}{3}x+y-7=\frac{8}{3}\] \[\frac{4}{3}x+y=\frac{8}{3}+7\] \[\frac{4}{3}x+y=\frac{29}{3}\]

Multiply both sides by $3$, since $A$, $B$, and $C$ must be integer values in standard form:

\[4x+3y=8\]

Note: If you are only given two points for a line, find the slope first using $m=\frac{y_1-y_2}{x_1-x_2}$, then proceed as with the example above, using one of the given points and the slope to write the equation for the line.

Using Values, Graphs, and Verbal Descriptions

You will also need to be able to write the equation of a line given a table of values, a graph, or a verbal description.

For example:

Suppose the initial cost of producing a product is $\$75$ and it costs $\$3.50$ to make each unit. Write an equation for the total cost, $C$, if you make $x$ units.

The increase of $\$3.50$ represents the rate of change in the total cost for making $x$ number of units, so $3.50$ is the slope. The initial cost of $\$75$ represents the $y$-intercept for the equation of the line since initially implies the $x$ equals zero units produced. Using the slope-intercept form for a line means our total cost equation is:

\[C(x)=3.50x+75\]

Direct Variation

When two variables directly vary with each other, one variable, the dependent variable, is a multiple of the other one, the independent variable. If $y$ is some multiple of $x$, we can write $y$ as $y = kx$, where the constant $k$ is called the constant of variation.

Suppose $y$ varies directly with $x$. If $y$ is $7$ when $x$ is $2$, what is $y$ when $x$ is $6$?

To find the constant of variation, substitute $y$ and $x$ into $y = kx$ to get:

\[7=k \cdot 2\] \[k=\frac{7}{2}\]

Now we have $y=\frac{7}{2}x$. When $x$ is 6, we can find $y$ by:

\[y=\frac{7}{2}\cdot 6\] \[y=21\]

Using a Parallel Line

You can find the equation of one line that is parallel to another line only knowing one point on that line. Remember, two parallel lines have the same slope.

Example:

What is the equation of a line in slope-intercept form that contains the point $(-3, 5)$ and is parallel to $y=\frac{7}{2}x+1$?

Since the lines are parallel, the slope of the line containing $(-3, 5)$ is also $\frac{7}{2}$. Now, using the point-slope form, the equation of our line is:

\[y-5=\frac{7}{2}(x+3)\] \[y-5=\frac{7}{2}x+\frac{21}{2}\] \[y=\frac{7}{2}x+\frac{31}{2}\]

Using a Perpendicular Line

You can also find the equation of one line that is perpendicular to another line when you only know one point on that line. Remember, two lines that are perpendicular have slopes that are negative reciprocals to each other. In other words, if the slope of one line is $-\frac{7}{4}$, the slope of a perpendicular line will be $\frac{4}{7}$.

For example:

What is the equation of a line in slope-intercept form that contains the point $(2, 4)$ and is perpendicular to $3x+y=-5$?

Putting $3x+y=-5$ in slope-intercept form, we have a line that has a slope of $-3$. Since the lines are perpendicular, the slope of the line containing $(2,4)$ is $\frac{1}{3}$. Now, using the point-slope form, we have the equation:

\[y-4=\frac{1}{3}(x-2)\] \[y-4=\frac{1}{3}x-\frac{2}{3}\] \[y=\frac{1}{3}x+\frac{10}{3}\]

Using the Axes

Remember that vertical lines have no slope (that is, the slope does not exist), and horizontal lines have zero for their slopes.

Vertical lines passing through the point $(x_1, y_1)$ are parallel to the $y$-axis and the equation will be $y= y_1$.

Horizontal lines containing the point are parallel to the $x$-axis, and the equation will be $x= x_1$.

Example:

Find the equation of a line in slope-intercept form that passes through the point $(-3, -7)$ and is parallel to the $x$-axis.

The slope of the line thru $(-3, -7)$ is zero. Since it is parallel to the $x$-axis, we have $y=-7$.

Writing Linear Inequalities of Two Variables

If a graph, table of values, or a verbal description is given for a linear inequality, you should be able to write the equation of the linear inequality.

Example:

Write, in slope-intercept form, the linear inequality for this graph.

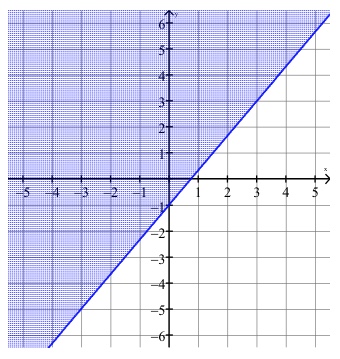
The graph has a $y$-intercept of $-1$ and the slope is $\frac{4}{3}$, since the rise over the run from the point $(0, -1)$ to the point $(3, 3)$ is $4$ over $3$. Now our line is represented by the equation, $y=\frac{4}{3}x-1$.

Since the graph of the inequality is shaded above the line, and the line is solid, our inequality now becomes:

\[y\ge\frac{4}{3}x-1\]

Writing Systems of Linear Equations

Lastly, if a graph, a table of values, or a verbal description is given for a system of two linear equations, you should be able to write equations for the system. Remember to put your equations in standard form.

For example:

A local high school sells tickets for a carnival to raise money for graduation. A total of $1575$ tickets are sold. The cost for a student ticket is $\$1.75$ and an adult is $\$3.25$. Funds raised from selling the tickets totaled $\$3575.50$. Write a system of equations, where $x$ is student tickets sold, and $y$ is adult tickets sold.

The sum of student tickets and adult tickets sold was $1575$, so we have $x+y=1575$. Also, the revenues raised by the student and adult tickets sold were $1.75x$ and $3.25y$, respectively. So, the total revenue raised is the sum of the revenues raised by the student and adult tickets sold, and we have $1.75x+3.25y=3575.50$. Our system is:

\[x+y=1575\] \[1.75x+3.25y=3575.50\]

We will solve this system in the next portion of this guide.

Solving and Evaluating

Once a linear equation or inequality is written, you will also need to know how to solve it.

Linear Equations in One Variable

Solve for $x$ using the order of operations as a guide if $6(x-2)+x-5=4-2(7-x)$.

Using PEMDAS to simplify both sides of the equation before isolating $x$, we get:

\[6(x-2)+x-5=4-2(7-x)\] \[6x-12+x-5=4-14+2x\] \[7x-17=-10+2x\] \[5x=7\] \[x=\frac{7}{5}\]

Linear Inequalities in One Variable

Remember to change the sign of the inequality when multiplying or dividing the inequality by a negative number.

For example:

Let $-5(2x-1)+x-4\le\,-3(7-x)+3$. Solve for $x$. Put your answer in interval notation.

\[-5(2x-1)+x-4\le\,-3(7-x)+3\] \[-10x+5+x-4\le\,-21+3x+3\] \[-9x+1\le3x-18\] \[-12x\le-19\] \[x\ge\frac{19}{12}\]

Systems of Linear Equations

You can solve a system of equations by substitution, where one equation is substituted into the other equation, or by elimination, where the two equations are combined in order to eliminate one variable in order to find the value of the other one.

Again, the problem:

A local high school sells tickets for a carnival to raise money for graduation. A total of $1575$ tickets were sold. The cost for a student ticket was $\$1.75$ and for an adult was $\$3.25$. The total amount raised by selling the tickets was $\$3575.50$. How many student and adult tickets were sold?

As we saw in the writing systems of linear equations lesson, we determined the system to have the equations:

\[x+y=1575\] \[1.75x+3.25y=3575.50\]

where $x=$ the number of student tickets and $y=$ the number of adult tickets sold.

Solving the system by the elimination process we have,

\[-1.75(x+y=1575)\] \[1.75x+3.25y=3575.50\]

then

\[-1.75x-1.75y=2756.25\] \[1.75x+3.25y=3575.50\]

so, by adding the two equations vertically, we have

\[0x+5y = 819.25\]

\[5y=819.25\] \[y=163.85\]

or approximately $164$ adult tickets were sold

Now, substituting back into one of the original equations, $x+164=1575$.

$x=1411$ student tickets were sold