Math Study Guide for the PERT

Working with Fractions

You need to know the terms numerator and denominator. In a fraction, the numerator is the top number, or the number that represents the part. The bottom number is the denominator, and it represents the whole.

Simplify/Lowest Terms

Simplifying fractions means reducing them to their lowest terms, and it makes it easier to work with them. Here is how we simplify $\frac {54}{81}$:

\[\frac {54}{81} =\require{cancel} \frac {2 \cdot \cancel{3} \cdot \cancel{9}}{3 \cdot \cancel{3} \cdot \cancel{9}} = \frac {2}{3}\]

As you can see, we’re left with a much smaller and more manageable fraction. This will make it easier to do various operations, including adding and subtracting.

Adding and Subtracting

To add fractions with the same denominators, add the numerators and copy the denominator. For example:

\[\frac {2}{5} + \frac {1}{5} = \frac {3}{5}\]

To add fractions with different denominators, first you have to find the least common denominator (also called the lowest common denominator). Once you have expressed the fractions as equivalent fractions with the least common denominator, you can proceed to addition.

To find the least common denominator, first list both denominators with a few of their multiples. Let’s say you want to add $\frac {3}{7}$ and $\frac {1}{3}$. You will need to find multiples of $7$ and $3$:

$7: \,\,\,7, \,14,\, 21,\, 28,\, 35$
$3: \,\,\,3, \,6, \,9,\, 12,\, 15,\, 18,\, 21$

Pick the number that is common to both lists; in this case, $21$. That is the common denominator. Now we can add the fractions:

\[\frac {3}{7} + \frac {1}{3} = \frac {9}{21} + \frac {7}{21} = \frac {16}{21}\]

Subtraction of fractions follows the same procedure as the addition of fractions.

Multiplying

The easiest operation with fractions is multiplication because you don’t need to worry about finding common denominators. Simply multiply the numerators by each other, then multiply the denominators by each other. If needed, reduce to the lowest terms:

\[\frac{3}{8} \cdot \frac{2}{5} = \frac{3 \cdot 2}{8 \cdot 5} = \frac{6}{40} = \frac{3}{20}\]

Dividing

To perform division involving two fractions, rewrite the second fraction in its reciprocal form and then follow the rules for multiplication:

\[\frac {5}{9} \div \frac{4}{3} = \frac {5}{9} \cdot \frac{3}{4} = \frac {15}{36} = \frac {5}{12}\]

Equivalent Fractions

Math questions involving fractions often entail reducing answers to their simplest form or lowest terms. The fraction $\frac {15}{45}$ can be reduced to $\frac {1}{3}$, which is in the simplest form (it can’t be reduced any further).

This can also be seen with the fractions $\frac{4}{12}$, $\frac{6}{18}$, and $\frac{2}{6}$. They are equivalent fractions because they all reduce to the same fraction ($\frac{1}{3}$). Equivalent fractions can be found by dividing the numerator and denominator by a common factor or by multiplying the numerator and denominator by a fraction equal to $1$, such as $\frac{3}{3}$.

Percent and Ratios

A percent indicates a number out of $100$; so, $5\%$ means $5$ out of $100$, or $\frac{5}{100}$. You can think of percent as per $100$. It can also be understood as a part of a whole. So to find out what percent of $60$ is $20$, write it first as $\frac{20}{60}$. Divide to find the ratio, and then multiply by $100$ to calculate the percentage. So, $20$ is $33.3\%$ of $60$.

Examples of percent problems:

\[\text{Percent Increase or Decrease}\]

In 24 hours, gasoline went from $\$3.44$ per gallon to $\$3.68$. By what approximate percent did the price change?

Percent change = $\frac{\text{difference}} {\text{original amount}} \times 100$.

Percent change = $\frac{3.68 - 3.44}{3.44} \times 100$

Percent change = $\frac{0.24}{3.44} = 0.0698 \times 100 \approx 7 \%$

A ratio is a different use for a fraction. Ratios are usually used to compare two quantities. For example, if a motorcycle engine is $65$ horsepower, and a scooter engine is $5$ horsepower, we can compare them by saying the ratio of their horsepower is $65$ to $5$. This can be written in a couple of different ways, $65:5$ or $\frac{65}{5}$. Just as with a fraction, we can simplify. Divide both numbers by $5$ to get $\frac{13}{1}$ or $13:1$.

If a $12\,\text{oz}$ box of Sugar-Buddies costs $\$ 5.30$, while at another store a $16\,\text{oz}$ box costs $\$6.40$, which is the better deal?

To answer, you’ll need to find the ratios of dollars to ounces for each box. You want the box with the lowest ratio:

$\frac{\$5.30}{12} = \$0.44$ cents per ounce

$\frac{\$6.40}{16} = \$0.40$ cents per ounce.

The $16\,\text{oz}$ box is the better deal.

A proportion is a statement of equality between two fractions, very often with one of the four terms being a variable, such as the one below:

\[\frac{3}{4} = \frac{5}{x}\]

These are solved by cross-multiplying, or multiplying in this pattern:

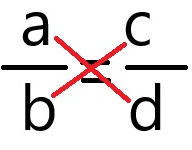
1 Cross-Multiplying fixed.png

This gives us $ad=bc$.

Using our example from above, we get:

\[3 \cdot x = 5 \cdot 4\] \[3x = 20\]

Divide both sides by $3$ to get $x$ alone, and you have:

\[x = \frac{20}{3} = 6 \frac{2}{3}\]

Comparing Rational Numbers

Recall that rational numbers include all integers and fractions, including decimal fractions. Comparing integers and decimals is not difficult for most of us because we understand place values. Comparing fractions is often not as easy. If two fractions have the same denominator, we can tell at a glance which is larger.

Which is larger, $\frac{5}{8}$ or $\frac{3}{8}$? It’s $\frac{5}{8}$ of course.

If the denominators are different, however, we have a choice. We can convert them to a common denominator as we do when we add or subtract fractions, or we can change each fraction into decimal form. Unless the fractions look fairly easy, it’s probably best to change them to decimals.

Which is larger, $\frac{3}{5}$ or $\frac{2}{3}$?

Changing both to decimals gives us $\frac{3}{5} =0.60$ and $\frac{2}{3}= 0.67$.

It’s now clear that $0.67$ is the larger decimal, so $\frac{2}{3}$ is the larger fraction.