Formulas You’ll Need to Know for Mathematics Questions on the HESI Test

Why Do Pre-Nursing Students Need to Know Math?

Mathematics is foundational in many professional fields, and nursing is no exception. Although you may not be administering medications or setting IV drip rates just yet, foundational math skills are essential for nursing school and your eventual nursing career. The HESI Mathematics test ensures you have the skills needed for success. Let’s dive into each of these areas and provide some practical examples.

Essential HESI Math Formulas

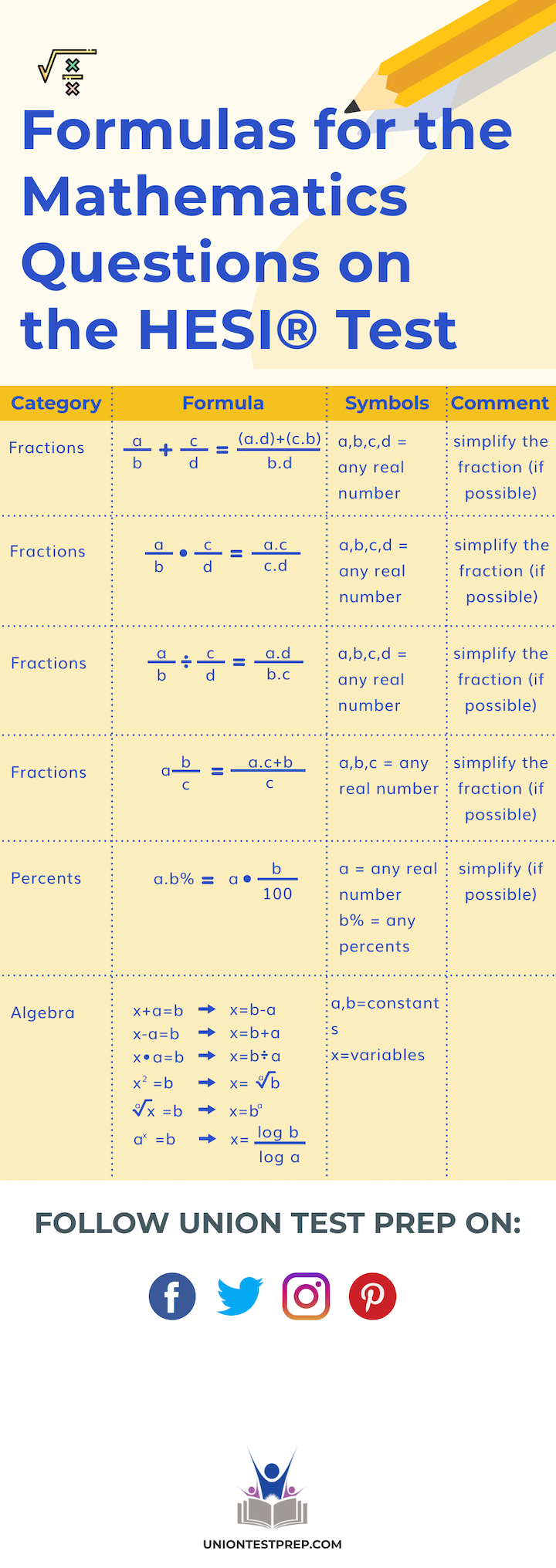
Before diving into detailed explanations of various math concepts, it’s crucial to arm yourself with some indispensable formulas. The table below encapsulates essential formulas, categorized by mathematical operations, that you’ll need to know for the HESI Mathematics section. Familiarizing yourself with these will not only streamline your problem-solving process but also bolster your confidence in handling a variety of questions.

\[\begin{array}{|c|c|c|c|} \hline \textbf{Category} & \textbf{Formula} & \textbf{Symbols} & \textbf{Comment} \\ \hline \text{Fractions} & \dfrac{a}{b} +\dfrac{c}{d} = \dfrac{(a\cdot d) + (c\cdot b)}{b\cdot d} & a,b,c,d = \text{any real number} & \text{simplify the fraction }\\ & & &\text{(if possible) } \\ \hline \text{Fractions} & \dfrac{a}{b} \cdot \dfrac{c}{d} = \dfrac{a\cdot c}{b\cdot d} & a,b,c,d = \text{any real number} & \text{simplify the fraction }\\ & & &\text{(if possible) } \\ \hline \text{Fractions} & \dfrac{a}{b} \div \dfrac{c}{d} = \dfrac{a\cdot d}{b\cdot c} & a,b,c,d = \text{any real number} & \text{simplify the fraction }\\ & & &\text{(if possible) } \\ \hline \text{Fractions} & a\frac{b}{c} = \dfrac{a\cdot c + b}{c} & a,b,c = \text{any real number} & \text{simplify the fraction }\\ & & &\text{(if possible) } \\ \hline \text{Percents} & a \cdot b \% = a \cdot \frac{b}{100} & a = \text{any real number} & \text{simplify} \\ & & b \% = \text{any percent} & \text{(if possible)} \\ \hline & x + a = b \rightarrow x = b-a & & \\ & x - a = b \rightarrow x = b+a & & \\ & x \cdot a = b \rightarrow x = b \div a & a, b = \text{constants} & \\ \text{Algebra} & x \div a = b \rightarrow x = b \cdot a & x = \text{variable} & \\ & x^a = b \rightarrow x = \sqrt[a]{b} & & \\ & \sqrt[a]{x} = b \rightarrow x = b^a & & \\ & a^x = b \rightarrow x = \dfrac{\log b}{\log a} & & \\ \hline \end{array}\]

Essential Math Concepts to Understand on the HESI

Fractions

A fraction is a number representing part of a whole. The top number, or numerator, represents the portion being considered, while the bottom number, or denominator, indicates the total number of equal parts that make up that whole.

Examples:

1. Adding Fractions: To add fractions with different denominators, you need to find a common denominator.

\[\frac{1}{3} + \frac{2}{5} = \frac{(1\cdot5) + (2\cdot3)}{3\cdot5} = \frac{5 + 6}{15} = \frac{11}{15}\]

1. Multiplying Fractions: When multiplying fractions, simply multiply the numerators together and the denominators together.

\[\frac{2}{3} \cdot \frac{4}{5} = \frac{2\cdot4}{3\cdot5} = \frac{8}{15}\]

1. Dividing Fractions: To divide one fraction by another, multiply the first fraction by the reciprocal (flipped version) of the second.

\[\frac{3}{4} \div \frac{5}{6} = \frac{3}{4} \cdot \frac{6}{5} = \frac{3\cdot6}{4\cdot5} = \frac{18}{20} = \frac{9}{10}\]

Percents

Percents are a way to express a fraction out of 100. Converting between fractions, decimals, and percents is a common task in math.

Examples:

1. Finding the Percent of a Number: To find, say, 25% of 80, you multiply 80 by \(\frac{25}{100}\).

   \[80 \times 25\% = 80 \times \frac{25}{100} = 20\]

2. Converting a Fraction to Percent: Convert \(\frac{3}{4}\) to a percent.

\[\frac{3}{4} = 3 \div 4 = 0.75 = 75\%\]

Basic Algebra

Algebra is about finding unknowns. Variables, usually represented by letters, stand in for unknown values. The goal is to determine their value.

Examples:

1. Solving for x in Addition:

\[x + 4 = 9 \implies x = 9 - 4 \implies x = 5\]

1. Solving for x in Multiplication:

   \[3x = 12 \implies x = \frac{12}{3} \implies x = 4\]

2. Using Exponents and Roots:

   \[x^2 = 49 \implies x = \sqrt{49} \implies x = 7\]

Remember, the HESI exam is testing your basic understanding of these concepts, so practicing them is essential. Use the formulas above and apply them to various problems to reinforce your understanding.

Tips and Techniques for Mastering HESI Mathematics

Now that you’re familiar with the key concepts tested in the HESI Mathematics section, it’s crucial to equip yourself with strategies to solve these problems efficiently and accurately. Here’s a guide to mastering the mathematical challenges you’ll encounter:

Tackling Fractions

Common Denominator is Key: Before adding or subtracting fractions, always ensure they have a common denominator. The least common multiple (LCM) of the two denominators can serve as the common denominator.

Reduce Whenever Possible: After performing operations with fractions, always look to reduce or simplify them to their lowest terms. This makes it easier to compare or further manipulate the fraction.

Visualize with Pie Charts: Sometimes, it helps to draw a quick pie chart to visualize fractions, especially if you’re unsure about your answer.

Playing with Percents

Shift Between Decimals and Percents: Get comfortable converting between decimals and percents. Remember: To convert a percent to a decimal, divide by 100. To convert a decimal to a percent, multiply by 100.

Use the 1% Technique: If you’re trying to find a tricky percentage of a number, find 1% of that number first, then scale up. For example, to find 7% of a number, first find 1% and then multiply it by 7.

Real-world Context: Always relate percentages back to real-world scenarios. This can make seemingly abstract problems more tangible.

Algebraic Acumen

Isolate the Variable: Your primary goal with algebraic equations is to isolate the variable. Whether you’re adding, subtracting, multiplying, or dividing, keep this endgame in mind.

Balance the Equation: Whatever operation you perform on one side of the equation, you must perform on the other. This maintains the equation’s balance.

Double-Check with Substitution: Once you think you’ve solved for the variable, plug it back into the original equation to ensure both sides are equal.

General HESI Math Strategies

Practice with Purpose

Consistency is the hallmark of successful test preparation. Tackling the free practice questions and using the provided flashcards can reinforce your understanding and highlight areas that need further revision. Remember, the goal is not just repetition but understanding.

Time is of the Essence

On the HESI, you’re typically allotted 50 minutes to complete the Mathematics section, which contains around 55 questions. This gives you just under a minute per question. Therefore, while deep understanding is essential, so is pacing. Developing a rhythm ensures you don’t get bogged down by challenging questions, allowing you adequate time for review. It’s a good idea to do a couple of timed HESI practice tests to get a feel for this rhythm.

Maintaining the Right Mindset

Mathematics, especially under timed conditions, can feel overwhelming. But remember: you’ve prepared, practiced, and you have the tools you need to succeed. Confidence in your skills and a calm demeanor can make the difference between recognizing a solution and overlooking it. During the exam, if a particular question seems too challenging, don’t hesitate to move on and come back to it later. Your subconscious might just work on it in the background.

Approaching HESI Mathematics Effectively

The HESI Mathematics section gauges your foundational understanding of key math principles. The challenges in this section, while demanding, become manageable with thorough preparation and a strategic mindset. Tackling each question methodically not only gears you for the exam but also lays a solid foundation for further studies in nursing. As you delve deeper into your HESI preparation, remember that a focused approach will serve you well, both now and in the future.