Mathematics Knowledge Study Guide for the ASVAB
Page 2
Algebra: Part 2
Equations and Inequalities
The activity most associated with algebra is probably solving for an unknown, and that unknown will be part of an equation. The other possibility is solving for an unknown in an inequality. Both are covered in the following sections.
Creating Equations for Word Problems
Word problems are no doubt the biggest source of frustration for math students. While no method can work every time, the steps below are a good way to deal with a word problem.
Read the problem at least twice. The more familiar you are with the problem, the more likely it is that sooner or later you will have an AHA! moment, where you suddenly see how to do it.
Circle or list what is given. For example: List price, \(p=12.95\); Discount rate \(r= 10\%\).
Look for key words that will tell you what to do, such as total, sum, difference, fewer, etc.
Know what you’re looking for and write it down. For example, Interest, \(i=\text{ ?}\).
Sometimes a picture helps, especially if the problem deals with physical things like area, volume, speed, depth, or distance.
Look back at recent formulas you may have used. Your problem probably uses one of those.
Basic Procedures for Solving
The ASVAB requires you to have a rudimentary knowledge of algebra and algebraic equations.
Steps to Follow
These steps will serve you well for equations that have only one variable, and the simplest quadratic equations. For example: \(2x^2=50\).
Consider the equation \(12+8t=10-2t+8\).
1. Isolate the variable: Get all the variable terms on one side of the equation (let’s say the left side) by using any of the properties of equality, and, in the same way, get all constant terms on the right side.
\[12-8t=10-2t+8\]Subtract \(12\) from both sides.
\[12-12-8t = 10 -2t +8 -12\] \[-8t=-2t+10+8-12\]Add \(2t\) to both sides.
\[-8t+2t=10+8-12\]Combine all the variable terms into a single variable term, and do the same thing with the constants.
\[-6t=6\]Get rid of any coefficient or divisor by either dividing both sides by the coefficient or multiplying by any divisor.
\[\dfrac{-6t}{-6} = \dfrac{6}{-6}\] \[t=-1\]2. Do the same thing to both sides: It’s important to always do any operations to both sides. It’s kind of a golden rule of mathematics: “Do to one side what you did to the other.”
3. Confirm the answer: Once you have an answer, always substitute it back into the original equation to make sure it works.
PEMDAS
Don’t forget PEMDAS either. When performing a series of mathematical operations, follow this order: Parentheses, Exponents (or powers and roots), Multiplication and Division (left to right), Addition and Subtraction (left to right).
\[7 + (8 \cdot 6^2 + 7)\] \[7 + (8 \cdot 36 + 7)\] \[7 + (288 + 7)\] \[7 + 295 = 302\]An easy way to remember PEMDAS is to memorize the phrase: Please Excuse My Dear Aunt Sally.
An Example:
Students may be required to solve for x (or other variable) in an equation, such as:
\[x + 8 = 35\]You always want to isolate the variable (x here) on one side of the equation so that your answer will be on the other side. To do this, you need to perform the opposite operation (attached to the number that needs removing) to both sides of the equation. This is how that would look for this problem:
\[x + 8 - 8 = 35 - 8\] \[x = 27\]Another example:
\[\frac{x}{4} = 8\]Here, the opposite operation of the division shown in \(\frac{x}{4}\) is multiplication. So:
\[4 \cdot \frac{x}{4} = 8 \cdot 4\] \[x = 32\]Square Roots and Reciprocals
You may also be asked to find the square root of a number or the reciprocal of a number. Study and practice completing basic algebraic equations to prepare yourself for this part of the Mathematics Knowledge test.
Equations with Two Variables
Given an expression with two variables, be able to evaluate the expression. Given an equation with two variables, be able to solve it in two different ways.
Evaluate an Expression When Given the Variable Values
To evaluate an expression means to substitute given values for the variables and then simplify the expression using PEMDAS.
If \(x=3\) and \(y=5\), evaluate \(x-5(y-2x)+9y\).
Substituting, we get:
\[3-5(5-6)+45\] \[3-5(-1)+45\] \[3+5+45\] \[53\]Solve for One Variable In Terms of Another
Any time you have an equation with two variables, one of those variables can be isolated, solving the equation for that variable.
Solve for \(r\) in terms of \(s\).
\[s(12-r) = 10\] \[12s-rs=10\] \[-rs=10-12s\] \[\dfrac{-rs}{-s}=\dfrac{10-12s}{-s}\] \[r=\dfrac{10-12s}{-s} \text{ or } -\dfrac{10-12s}{s}\]Systems of Equations
A system of equations is one in which there are two or more equations with the same solutions. The type you are likely to see will have two equations in two variables. They will look like this:
\(2x-y=-1\)
\(4x+2y=18\)
Substitution
One way to solve a system of equations is by substitution. Here’s how it works.
Given these two equations, solve for \(x\).
\(3x+2y=-1\)
\(2x+y=1\)
Step 1: Use one of the equations to solve for one of the variables in terms of the other. Let’s choose the second equation and solve for \(y\), because it looks easy.
\[2x+y=1\] \[y=1-2x\]Step 2: Now we take the value we just got for \(y\), substitute it into the first equation. \(3x+2y=-1\), and solve for \(x\):
\[3x+2(1-2x)=-1\] \[3x +2-4x=-1\] \[3x-4x=-1-2\] \[-x=-3\] \[x=3\]Solving with Elimination (Also Called Combination)
In this method we add the two equations to each other, or subtract one from the other in order to get one variable to drop out. Then we solve the resulting one-variable equation. This example is pretty easy, but it will show the method.
\(3a+3b=9\)
\(a-3b=11\)
Do you see that if you add the two equations together, the \(b\) terms will drop out? See below.
\[\begin{array}{rrrr} 3a & +3b&=&9\\ + a& -3b & =&11\\ \hline 4a&&=&20\\ &a&=5 \end{array}\]Here is an example with a little twist.
\(3a+2b=11\)
\(2a+b=8\)
Adding or subtracting here won’t make either variable drop out. But, we have a trick. We will multiply the second equation by \(-2\) and then add them together.
\[\begin{array}{rrrr} 3a & +2b&=&11\\ + (-4a)& -2b & =&-16\\ \hline -a&&=&-5\\ &a&=&5 \end{array}\]Backsolving
Backsolving is what you do after you have solved for one variable, and want to solve for the other one. All you do is take the value you solved for and substitute it back into either of the original equations and then solve that. See below.
\(3a+2b=11\)
\(2a+b=8\)
Take the two equations we just solved. We got \(a=5\). Substitute \(5\) in for \(a\) in the first equation and solve for \(b\).
\[3(5)+2b=11\] \[15+2b=11\] \[2b=-4\] \[b=-2\]Now we have a complete solution to the system of equations: \(a=5\) and \(b=-2\).
Consistent and Inconsistent Systems
If a system of equations has one solution, the system is called consistent, and the graphs of the two equations intersect. If the system has no solution, it is called inconsistent and the graphs will be parallel.
Quadratic Equations with Variables
Graphs of quadratic equations are parabolas. Terms and methods of dealing with quadratics and their graphs are listed below.
Standard and Vertex Forms
The standard form of a quadratic equation is \(y=ax^2+bx+c\), where \(a, b,\) and \(c\) are constants and \(a \neq 0\). This can be used to plot points and develop the associated graph. Parabolas of this form can open upward or downward. If \(a \gt 0\), the parabola opens upward. If \(a \lt 0\), it opens downward.
A good term to know is the vertex of the parabola. For an upward opening parabola, it is the lowest point of the parabola. For a downward opening parabola, the vertex is the highest point.
There is another form that can be useful for visualizing the graph called the vertex form. If you have a quadratic in the form \(y-k=a(x-h)^2\), the vertex will be the point \((h, k)\).
For example, if you have the equation \(y-3=2(x-5)\), the vertex of its parabola will be the point \((5, 3)\). Many times the equation may not be in that form, so you need to use your algebra skills to put it in that form.
Keep a close eye on the signs. If the equation was \(y+3=2(x+5)\), the vertex would be \((-5, -3)\).
Axis of Symmetry
For the graph of \(y=ax^2+bx+c\), there is a line that perfectly divides the parabola in half. It’s called the axis of symmetry. See the example below. The axis is the vertical line that passes through \((0,-2)\). Notice that the axis of symmetry goes right through the vertex.
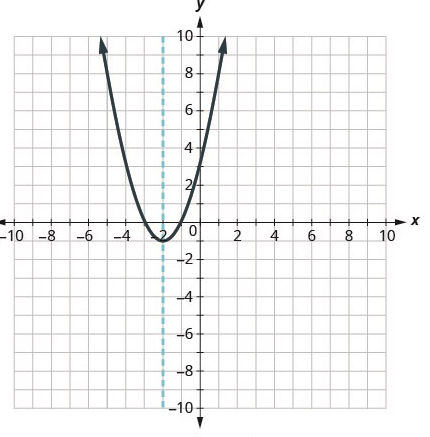
Retrieved from: https://openstax.org/books/intermediate-algebra-2e/pages/9-6-graph-quadratic-functions-using-properties
This is a graph of \(y=x^2+4x+3\). A good thing to know is that the equation for the axis of symmetry is:
\[x=\frac{-b}{2a}\]For this equation, that would give us \(x=\frac{-4}{2 \cdot 1}\) which is \(x=-2\).
Solving by Factoring
We saw how to factor quadratic expressions earlier in this guide. We actually did it earlier in the polynomial section. Here is another quick look at the process.
Consider the equation \(x^2-x-12=0\).
We can factor it and get \((x-4)(x+3)=0\). If you have two factors that give you zero when they’re multiplied, at least one of them must be zero.
If the first factor is zero, we can write:
\(x-4=0\) and therefore \(x=4\)
If the second factor is zero, we can write:
\(x+3=0\) and therefore \(x=-3\)
In this way, we see that if \(x\) is \(4\) or \(-3\), then the given expression will equal zero, so the solutions to the given equation are \(4\) and \(-3\).
Completing the Square
Suppose you need to solve the quadratic \(x^2-6x-3=0\). Factoring isn’t going to work here, so we need a different trick. That trick is called completing the square. The aim is to try to get a quadratic that is a perfect square on the left and then take the square root of both sides.
\[x^2-6x-3=0\]First step—Add \(3\) to both sides to move the \(-3\) out of the left side:
\[x^2-6x =3\]*Second step—Take half of \(-6\), square it, add it to both sides and factor the left side:
\[x^2 -6x +9 = 3+9\] \[(x-3)^2 = 12\]Third step—Take the square root of both sides:
\[\sqrt{(x-3)^2} = \sqrt{12}\] \[x-3=2\sqrt{3}\] \[x=3+2\sqrt{3}\]Roots and Zeros
Roots and zeros are very closely related and are easily confused.
For an equation that is set equal to zero, the root(s) of that equation are the values for the variable that make the equation true.
For the equation \(x^2-6x+5=0\), both \(x=5\) and \(x=1\) make the equation true, so they are the roots of the equation.
For a polynomial, the zeros of the polynomial are the values that, if you set it equal to zero and solved it, would make it true.
For the polynomial \(x^2-6x+5\), the zeros would be \(x=5\) and \(1\).
To summarize, the zeros of \(ax^2+bx+c\) are the roots of \(ax^2+bx+c = 0\).
Discriminants: How Many Solutions?
Quadratic equations often have two roots, but sometimes they have only one, or none at all. If you want to know how many roots a certain quadratic equation has, there is a formula you can use. It’s called the discriminant. Using the standard form of a quadratic equation, \(ax^2+bx +c=0\), the discriminant is \(\sqrt{b^2-4ac}\).
The discriminant has three possible outcomes:
If it is positive, there are two roots.
If it is zero, there is one root.
If it is negative, there are no real roots.
Let’s try it on this equation: \(x^2+4x+4=0\), where \(a=1, b=4, c=4\).
\[\sqrt{4^2-4 \cdot 1 \cdot 4}\] \[\sqrt{16-4 \cdot 1 \cdot 4}\] \[\sqrt{16-16} =0\]So the given equation has only one solution.
The Quadratic Formula
Although factoring and completing the square can help solve quadratics, many quadratics won’t be easily factorable and completing the square cannot always be easily done. Luckily, we can always use the quadratic formula. It is based on the standard form \(ax^2+bx+c=0\).
This is it:
\[x=\dfrac{-b \pm\sqrt{b^2-4ac}}{2a}\]Given any quadratic equation, we can substitute the values of \(a, b, \text{ and } c\) into the quadratic formula. We will use it on the equation below:
\[5x^2+3x-2=0\]We see that \(a=5, b=3, \text{ and } c=-2\), so we will substitute those into the quadratic formula:
\[x=\dfrac{-3 \pm\sqrt{3^2-4 \cdot 5 \cdot (-2)}}{2 \cdot 5}\]And simplify:
\[x=\dfrac{-3 \pm\sqrt{9+40}}{10}\] \[x=\dfrac{-3 \pm\sqrt{49}}{10}\] \[x=\dfrac{-3 \pm7}{10}\] \[x=\dfrac{-3 +7}{10} \text{ or } x=\dfrac{-3 -7}{10}\] \[x=\dfrac{4}{10} \text{ or } x=\dfrac{-10}{10}\] \[x=\dfrac{2}{5} \text{ or } x = -1\]Inequalities
After working with equations, inequalities probably seemed a little odd to you the first time you saw them. These reminders should bring you back up to speed on them.
Inequality Signs
There are four inequality signs that you should know:
\[\begin{array}{l} \lt \quad \text{ less than}\\ \gt \quad \text{ greater than}\\ \leq \quad \text{ less than or equal to}\\ \geq \quad \text{ greater than or equal to}\\ \end{array}\]Showing Inequalities on the Number Line
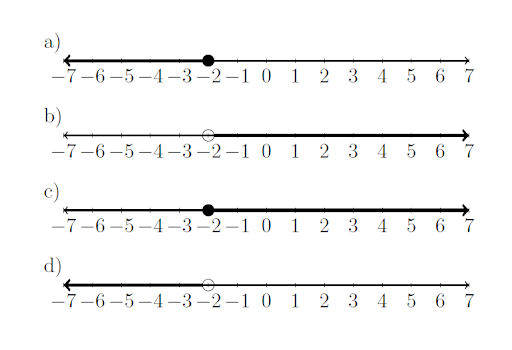
When graphing inequalities on a number line, remember the arrow goes to the left for a “less than” statement and to the right for a “greater than” statement. Also, a solid dot means that point is included in the graph (used with “or equal to” statements). A hollow dot means that point is not included in the graph.
The “a” graph below shows the graph of \(x \leq-2\).
The “b” graph shows the graph of \(x \gt -2\).
The “c” graph shows the graph of \(x \geq -2\).
The “d” graph shows the graph of \(x \lt -2\).
Solving Inequalities
Inequalities can be solved just like equations. The big difference is that inequalities give you a whole range of solutions, like \(x \gt 7\), instead of just one or two solutions. We’ll do two examples.
Example 1:
Solve \(4x+7 \leq3x-3\).
Just as with equations, you can add to, subtract from, multiply, or divide both sides of the inequality by any number. See the second example for one big exception to this rule.
In this example you can see that we subtracted \(3x\) and \(7\) from both sides.
\[\begin{array}{rrcrr} 4x&+7& \leq&3x&-3\\ -3x&-7& &-3x&-7\\ \hline & x & \leq& -10&\\ \end{array}\]Example 2:
In this example, the last step is to divide both sides by \(-3\). Notice that we flipped the inequality sign from < to >. This is what you do if you multiply or divide both sides by a negative number.
\[\begin{array}{rrcrr} 2x&+3& \lt&5x&-18\\ -5x&-3& &-5x&-3\\ \hline &-3x & \lt& -21&\\ -3x &\div -3 &\gt& -21 &\div -3&\\ &x &\gt &7&\\ \end{array}\]Compound Inequalities
A compound inequality is one that states two different conditions for the inequality. For example, we could state that we want the set of numbers that are greater than or equal to \(-2\) and less than \(5\). It could be written like this: \(-2 \leq x \lt 5\). The graph of that is below. Remember, a solid dot means that point is included because the inequality stated \(-2\) is less than or equal to \(x\).
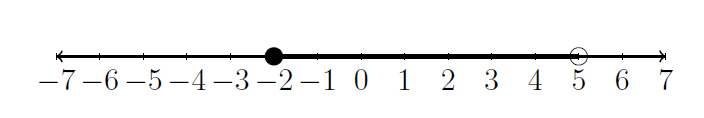
A different compound inequality is the set of numbers that are less than or equal to \(-2\) or greater than \(5\). The graph of this is below:
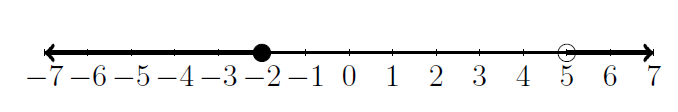
All Study Guides for the ASVAB are now available as downloadable PDFs