Free Study Guides for the
TSIA2
The TSIA2 is mandated for students entering college in the state of Texas, and the results will guide your course enrollment process. Find out what you need to know to do well on this test by using our FREE study guides for the TSIA2. This way, you’ll know what you’re facing ahead of time and can hone your skills, saving you both money and time in college.
Start here
Select a Study Guide to begin
These Study Guides are also available for download.
Sign up
Table of Contents
Sections of the TSIA2
ELAR: Reading
Being able to read with good comprehension is a vital skill if you want to perform well in college-level classes. The reading questions on the TSIA2 ELAR test assess all sorts of skills that contribute to the successful reading you will need to do as you pursue further education. Review all the information in this study guide to refresh your memory of reading skills you learned and/or need to practice before the test.
ELAR: Writing
Equally tested in the TSIA2 ELAR tests is the area of writing. Writing occupies half of the ELAR questions on both the CRC and Diagnostic TSIA2 tests, with reading being tested by the other half. Be sure to consult this study guide to see what kinds of things you’ll need to know about the best practices in writing.
Mathematics: Algebraic Reasoning
An important part of math involves skills you learned in Algebra classes. We know there were many procedures and methods covered and you’ll need to review what you learned. This study guide outlines the concepts and skills tested that require algebraic reasoning. Also be sure to access our practice questions and flashcards as you prepare.
Mathematics: Geometric and Spatial Reasoning
General Information
You will find questions about the following areas of math on both the TSIA2 CRC and the Diagnostic Test:
Both tests cover the same skills and you’ll need to take the Diagnostic Test if you make a certain score range on the CRC. You won’t know this until after the CRC is complete, so you’ll need to prepare as if you are going to take both tests.
There will be three questions about geometric and spatial reasoning on the CRC, and the Diagnostic Test will have 12 questions about this area of math. In this study guide is an outline with explanations of all the geometric and spatial reasoning skills tested. Our other three study guides for the TSIA2 Mathematics Test cover the remaining math areas on this test. Be sure to check out our practice questions and flashcards for complete preparation and seek additional help in any areas in which you still struggle.
You will only see multiple-choice questions on these math tests.
Basic Geometry Concepts
Geometry is the study of two-dimensional and three-dimensional space and the properties of the lines, angles, and shapes in that space. Here are some concepts you’ll need to know about:
Lines and angles form the basis of many shapes in geometry.
Point— A point is a one-dimensional location on the plane. It has no length or width. Points are usually labeled with letter names.
Line— A line is a set of points that connect and pass through a designated pair of points. For any two given points, there is only one line that passes through them. A line extends indefinitely in both directions. Lines, rays, and segments are labeled with two points.
Ray— A ray is part of a line starting at a given point and extending in one direction only.
Line segment— A line segment connects two points but does not extend beyond them. It has a finite length.
Parallel— Parallel lines never intersect no matter how far out along the lines you look. They always remain at the same distance apart from each other.
Perpendicular— Perpendicular lines form 90 degree angles. If lines AB and CD are perpendicular, it is written as:
\[\overleftrightarrow{\text{AB}} \perp \overleftrightarrow{\text{CD}}\]Measurement Systems
You will likely encounter two different systems of measurement on this test: the U.S. Customary System, with pounds, feet, and inches, and the International System of Units, commonly known as the SI or metric system, with meters and kilograms.
Measuring Length
Although there are many sophisticated ways to measure length, it is commonly measured by closely comparing an object to a standard physical device like a ruler, tape measure, yard stick, or meter stick.
U.S. Standard Measurement
As mentioned above, in the U.S. we are used to using U.S. Customary units for measuring. Length can be measured in inches (in), feet (ft), yards (yd), or miles (mi). Here are some basic conversions:
1 foot = 12 inches
1 yard = 36 inches or 3 feet
1 mile = 5,280 feet or 1,760 yards
Metric Units
Most of the world uses the SI system units for measuring. Length can be measured in millimeters (mm), centimeters (cm), meters (m), or kilometers (km), to mention the basic units.
1 m = 100 cm
1 m = 1000 mm
1 km = 1000 m
Measuring Area
Areas of different figures are calculated in different ways, but always involve multiplying two length units, giving square units for the result.
U.S. Standard Measurement
Areas can be measured in squared length units, such as square inches (\(\text{in}^2\)) or square feet (\(\text{ft}^2\)).
\[\begin{array}{c} 1 \text{ ft}^2 = 12 \text{ in} \times 12 \text{ in} = 144 \text{ in}^2 \\ 1 \text{ yd}^2 = 3 \text{ ft} \times 3 \text{ ft} = 9 \text{ ft}^2\\ \end{array}\]Metric Units
Areas can also be measured in squared metric length units, such as square centimeters (\(\text{cm}^2\)) or square meters (\(\text{m}^2\)).
\[\begin{array}{c} 1 \text{ m}^2 = 100 \text{ cm} \times 100 \text{ cm} = 10,000 \text{ cm}^2 \\ 1 \text{ cm}^2 = 10 \text{ mm} \times 10 \text{ mm} = 100 \text{ mm}^2\\ \end{array}\]Measuring Volume
Volumes of different three-dimensional figures are calculated in different ways, but always involve multiplying three length units, giving cubic units for the result.
Standard Measurement
Volume can be measured in cubed length units, such as cubic inches (\(\text{in}^3\)) or cubic feet (\(\text{ft}^3\)), as well as in cups, quarts, gallons, and others.
\(1 \text{ ft}^3 = 12 \text{ in} \times 12 \text{ in} \times 12 \text{ in} = 144 \text{ in}^3\) \end{array}
Metric Units
Volume can be measured in cubed length units, such as cubic centimeters (\(\text{cm}^3\) or \(\text{cc}\) in medical usage) or cubic meters (\(\text{m}^3\)), as well as in liters (L) or milliliters (mL).
\[1 \text{ m}^3 = 100 \text{ cm} \times 100 \text{ cm} \times 100 \text{ cm} = 1,000,000 \text{ cm}^3\] \[1 \text{ cm}^3 = 10\text{ mm} \times 10 \text{ mm} \times 10\text{ mm} = 1,000 \text{ mm}^3\]Measuring Weight
U.S. Standard Measurement
We use pounds (lb), ounces (oz), and tons (tn) for weight. The word ton is sometimes written out, rather than using the only slightly shorter tn.
\[\begin{array}{c} 1 \text{ lb} = 16 \text{ oz} \\ 1 \text{ ton} = 2000 \text{ lb}\\ \end{array}\]Metric Units
Weight (mass, to be perfectly correct) can be measured in milligrams (mg), grams (g) or kilograms (kg).
\[\begin{array}{c} 1 \text{ kg} = 1000 \text{ g} \\ 1 \text{ g} = 1000 \text{ mg}\\ \end{array}\]Measuring Time
It’s probably safe to say that everyone knows that time is measured with a clock and that the basic units of time are seconds (s or sec), minutes (m or min), and hours (h or hr).
Standard Time Measurement
The base unit of time is the second in both the U.S. Customary System and the metric system. It follows that hours and days are also the same in both systems. Time notation that is commonly used is in the format hh:mm:ss in which hh is the number of hours, mm is the number of minutes, and ss is the number of seconds.
Military Time
Military time uses a four-digit 24-hour notation for the time of day. The format is hhmm in which hh is the number of hours that have elapsed since midnight and mm is the number of minutes that have elapsed since the start of the hour.
\[\begin{array}{c|c} \text{Military Time} & \text{Civilian Time}\\ \hline 0000 & \text{Midnight}\\ 0600 & 6:00 \text{AM}\\ 1200 & \text{Noon}\\ 1800 & 6:00 \text{PM}\\ 1430 & 2:30 \text{PM}\\ \end{array}\]Measuring Temperature
Most of the world uses the Celsius temperature scale, but common practice in the U.S. is to use the Fahrenheit scale. The Kelvin scale is often used in science, but isn’t common elsewhere. The figure below shows how the scales compare.
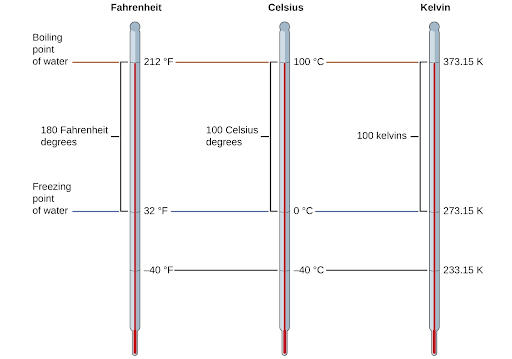
Retrieved from: openstax.org/books/chemistry-2e/pages/1-6
Unit Conversions within a Measurement System
One way to handle unit conversions is to write a proportion. You will know three of the terms and can write the proportion using those and solve for the fourth term. For example, let’s convert \(60\) inches to yards.
We know that \(1\) yd is \(36\) inches. Those two quantities will make a ratio that goes on one side of the proportion. On the other side will go our given quantity and a variable to represent the quantity to be solved for.
\[\dfrac{60 \text{ in}}{x \text { yd}} = \dfrac{36 \text{ in}}{1 \text{ yd}}\]Notice that the same unit appears on top in both ratios. That is one way to make sure that you’ve written the proportion correctly.
The next step is to cross multiply and then solve for \(x\). We’ll temporarily leave the units out for clarity.
\[36 x = 60\] \[x = \dfrac{60}{36} = \dfrac{5}{3} \text{ yd}\]For a second example, suppose we have a rectangle that is \(150\) cm by \(200\) cm. What is its area in square meters?
We can either convert each dimension into meters and then multiply them or we can multiply them and then convert \(\text{cm}^2\) to \(\text{m}^2\). Let’s use the second way because it has only one conversion.
\[150 \text{ cm} \times 200 \text{ cm} = 30,000 \text{ cm}^2\] \[\dfrac{30,000 \text{ cm}^2} {x} = \dfrac{10,000 \text{cm}^2}{1 \text{ m}^2}\]Cross multiply the numbers.
\[10,000 x = 30,000\] \[x= 3 \text{ m}^2\]Mathematics: Probabilistic and Statistical Reasoning
With advances in technology, knowledge of statistical skills is becoming increasingly necessary and useful. This study guide will help you review concepts that will be tested on the TSIA2 Mathematics tests. That way, you’ll know what you still need to study and can show what you really know on the tests.
Mathematics: Quantitative Reasoning
Questions in this area of math involve thinking and solving problems concerning amounts of things, using various operations and procedures. On the TSIA CRC test, you will see six questions of this type, and on the Diagnostic test, there will be 12. This is just one of the four math areas covered by both tests and we have study materials for all of them, so be sure to prepare completely. We’ve also provided enough practice questions for you to simulate test day, even if you need to take both the CRC and Diagnostic tests.

Hopefully, our study guides helped you narrow down what you needed to study before taking the TSIA2 and you are prepared to show your finest work on test day. Please let us know about your whole preparation and testing experience by finding us on Twitter, Facebook, Pinterest, Instagram, or YouTube. We can also be reached at info@uniontestprep.com if email is your thing.