Upper Level: Quantitative Reasoning Study Guide for the ISEE
Page 2
More Numbers and Operations
Types of Numbers
Numbers can be classified as real or imaginary. Real numbers include whole, rational (numbers that can be written as fractions or ratios), or irrational (such as pi and most roots) numbers.
Familiarity with various types of numbers will facilitate answering questions such as this example:
Which of the following choices correctly sorts these numbers from the least to the greatest value?
\[-\frac{3}{5}, \;\;0.5, \;\;-\frac{6}{9}, \;\;\pi, \;\;\sqrt{5}, \;\;3^{-1}, \;\;2 \cdot 10^{-4}\]
Answer:
Let’s write out the numbers in decimal form so it will be easier to compare.
Using division, \(- \frac{3}{5}\) can be written as:
\[- (3 \div 5)\] \[= - 0.6\]\(0.5\) is already in decimal form.
\(- \frac{6}{9}\) can be written as:
\[- (6 \div 9)\]\(= -0.67\) (rounded to two decimal places)
\(\pi\), rounded to two decimal places, is \(3.14\).
\(\sqrt{5}\), rounded to two decimal places, is \(2.24\).
\(3^{-1}\) can be written as:
\[\frac{1}{3^{1}}\] \[= \frac{1}{3}\]\(= 0.33\) (rounded to two decimal places)
\(2 \cdot 10^{-4}\) can be expanded and written as \(0.0002\).
Therefore, in decimal form, we have the numbers \(-0.6, \,0.5, \,-0.67, \,3.14, \,2.24, \,0.33\) and \(0.0002\).
We can now put the original numbers in order from least to greatest:
\[-\frac{6}{9}, \,-\frac{3}{5}, \,2 \cdot 10^{-4}, \,3^{-1}, \,0.5, \sqrt{5}, \,\pi\]Ratio and Proportion
Ratios are used to compare values. When comparing two or more values, part-to-part ratios or part-to-whole ratios can be used. Most ratio questions can be solved with logic and very minimal computation, such as in this example:
The ratio of boys to girls in a class of 50 students is 2:3. The students need to create 10 groups where each group must have an equal number of boys as there are girls. How many girls will not be included in the groupings?
The ratio of boys to girls to total is 2 : 3 : 5
From this ratio and the given total, we know that there are 20 boys : 30 girls : 50 total
To create 10 groups with equal number of boys and girls 20 boys : 20 girls : 40 total
Obviously, there will be a surplus of 10 girls who can’t be grouped as specified.
When we say that a ratio is in proportion (or is proportional) to another, we mean that the two ratios are equal. The corresponding sides of similar triangles, for example, are proportional. Knowing the dimensions of a triangle will, therefore, help solve the dimensions of a triangle similar to it. This is the same principle used for scaling on maps.
Fractions
Part-to-whole ratios can also be written as fractions. In the previous example, the ratio of the boys for every \(5\) students is \(2 : 5\). This can also be stated as “\(\frac{2}{5}\) of the class of \(50\) students is made up of boys”. The numerator \(2\) represents the part, while the denominator \(5\) represents the whole.
The fraction \(\frac{2}{5}\) is a proper fraction because the numerator is less than the denominator (and the value of the fraction is less than \(1\)).
Learn about improper, mixed, and equivalent fractions, as well.
- Improper fraction: A fraction where the numerator (top number) is greater than the denominator (bottom number).
For example, \(\frac{11}{5}\) and \(\frac{7}{2}\) are improper fractions.
- Mixed number: A whole number and a proper fraction combined together. It usually represents a number in between two whole numbers. Mixed numbers are also known as mixed fractions.
For example, \(2 \frac{1}{2}\) and \(3 \frac{3}{4}\) are mixed numbers.
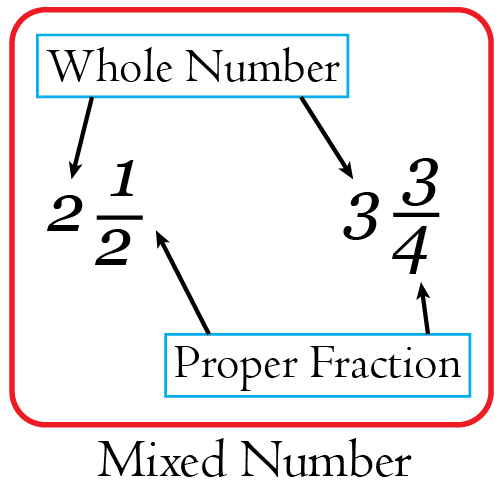
Note: A proper fraction is a fraction whose numerator is less than its denominator.
Equivalent fractions: When two or more fractions represent the same value when simplified, they are known as equivalent fractions. They will have different numerators and/or denominators.
For example, \(\frac{3}{4}\) and \(\frac{12}{16}\) are equivalent fractions. If we divide both the numerator and denominator of \(\frac{12}{16}\) by \(4\), we get the first fraction, \(\frac{3}{4}\). Thus, they are equal.
Also, the fractions \(\frac{7}{14}\) and \(\frac{4}{8}\) are equivalent fractions. Both fractions reduced to their lowest terms are \(\frac{1}{2}\).
It is also important to know how to determine the greatest common factor (GCF); this is used when simplifying fractions.
The greatest common factor (GCF) is the largest number that is a common factor of two or more numbers. To find the GCF of two numbers, we list all the factors of both numbers, circle the common factors, and select the largest of them.
For example, let’s find the GCF of \(12\) and \(16\).
List all the factors of \(12\) and \(16\):
\[12 : 1, \,2,\, 3,\, 4,\, 6, \,12\] \[16 : 1,\, 2,\, 4,\, 8, \,16\]The common factors of \(12\) and \(16\) are \(1, \,2,\) and \(4\). The largest of them is \(4\). Thus, the greatest common factor of \(12\) and \(16\) is \(4\).
We can use the greatest common factor method to simplify fractions. With the example below, we can reduce the fraction \(\frac{20}{25}\) to its lowest terms using the GCF method.
First, we list out all the factors of the numerator (\(20\)) and denominator (\(25\)):
\[20 : 1, \,2, \,4,\, 5, \,10, \,20\] \[25 : 1,\, 5, \,25\]Looking at the list, the common factors of both numbers are \(1\) and \(5\). The greatest of them is \(5\). Thus, the GCF of \(20\) and \(25\) is \(5\).
To reduce the fraction \(\frac{20}{25}\) to its lowest terms, we divide both the numerator and the denominator by the greatest common factor, \(5\):
\[\frac{20}{25} = \frac{20 \div 5}{25 \div 5} = \frac{4}{5}\]So, the fraction \(\frac{20}{25}\) reduced to its lowest terms is \(\frac{4}{5}\).
Learn how to find the least common multiple (LCM); this is useful when comparing fractions and when performing addition and subtraction of fractions.
The least common multiple (LCM) of two numbers is the smallest number that is divisible by both numbers. There are a couple of ways to figure out the LCM of two numbers, but we will look at the simplest way.
To find the LCM of two numbers, we write out some multiples of both numbers. Then, we select the common multiples. The LCM of the two numbers is the smallest of the common multiples.
For example, let’s find the LCM of \(6\) and \(8\).
List some multiples of \(6\) and \(8\):
\[6 : 6, \,12, \,18,\, 24, \,30, \,36, \,42, \,48, \,54, \,60, …\] \[8 : 8,\, 16,\, 24,\, 32, \,40,\, 48,\, 56, \,64, \,72, \,80, …\]We can see that the common multiples of \(6\) and \(8\) are \(24, 48\), and so on. Out of these, the smallest is \(24\). So, the LCM of \(6\) and \(8\) is \(24\).
We can use the LCM method to compare fractions. Let’s compare the fractions \(\frac{3}{4}\) and \(\frac{2}{3}\).
Since both fractions have unlike denominators, we first need to give them common denominators. For that, we will take the LCM of both denominators, \(4\) and \(3\).
Some multiples of \(3\) are:
\[3 : 3, \,6, \,9, \,12, \,15, \,18,\, 21, \,24, …\]Some multiples of \(4\) are:
\[4 : 4, \,8, \,12, \,16,\, 20, \,24, …\]Out of these, the common multiples are \(12\) and \(24\). The smallest is \(12\). Hence, the LCM of \(3\) and \(4\) is \(12\). Now, we convert the original fractions we are comparing to fractions with a denominator of \(12\).
\[\frac{3}{4} \times \frac{3}{3} = \frac{9}{12}\]and
\[\frac{2}{3} \times \frac{4}{4} = \frac{8}{12}\]So, comparing \(\frac{9}{12}\) and \(\frac{8}{12}\), we can see that \(\frac{9}{12} > \frac{8}{12}\). Thus, we can say \(\frac{3}{4} > \frac{2}{3}\).
Using the LCM method, we can also add and subtract fractions. The process is similar for both operations. First, we find the LCM of the two denominators of the two fractions, then rewrite the fractions using the same denominator, and then add or subtract. Let’s take a look at two examples below.
Example 1:
Add: \(\frac{1}{5} + \frac{3}{4}\)
Solution: First, let’s find the LCM of \(5\) and \(4\):
\[5 : 5, \,10, \,15, \,20, \,25, \,30, \,35, \,40, \,45, \,50, …\] \[4 : 4,\, 8, \,12, \,16,\, 20, \,24, \,28, \,32,\, 36, \,40, \,44, …\]The common multiples are \(20\) and \(40\). The smallest is \(20\). Hence, the LCM of \(5\) and \(4\) is \(20\). Let’s rewrite the fractions using a denominator of \(20\) and add:
\[\left(\frac{1}{5}\right)\left(\frac{4}{4}\right) + \left(\frac{3}{4}\right)\left(\frac{5}{5}\right)\] \[= \frac{4}{20} + \frac{15}{20}\] \[= \frac{4+15}{20}\] \[= \frac{19}{20}\]Example 2 :
Subtract: \(\frac{5}{8} - \frac{1}{3}\)
Solution: First, let’s find the LCM of \(8\) and \(3\):
\[8 : 8, \,16, \,24, \,32, \,40, \,48,\, 56, \,64, \,72,\, 80 …\] \[3 : 3,\, 6,\, 9, \,12, \,15, \,18, \,21, \,24, \,27, \,30, \,33, \,36, …\]The common multiple is \(24\), which is definitely the lowest. Hence, the LCM of \(8\) and \(3\) is \(24\). Let’s rewrite the fractions using a denominator of \(24\) and subtract:
\[\left(\frac{5}{8}\right)\left(\frac{3}{3}\right) - \left(\frac{1}{3}\right)\left(\frac{8}{8}\right)\] \[= \frac{15}{24} - \frac{8}{24}\] \[= \frac{15-8}{24}\] \[= \frac{7}{24}\]Decimals
The concept of decimals is an extension of the subject of fractions. The fraction \(\frac{1}{10}\) is the same as the decimal \(0.10\). Make sure you can convert decimals to fractions and percentages with ease. Without a calculator, some questions that include decimals can be more easily solved using fractions. Multiplying \(\frac{1}{4}\) by \(\frac{3}{4}\) is far simpler and quicker than multiplying \(0.25\) by \(0.75\) manually.
Your math skills must also include the ability to add, subtract, multiply, divide, and raise decimals to powers.
Percents
Percent means per hundred, so \(1\%\) means “\(1\) per hundred” or “\(\frac{1}{100}\)” or “\(0.01\)”. It could also refer to a scale or ratio of “\(1\text{:}100\)”. You must develop the skill of translating from percent to ratios, fractions, and decimals, depending on the context in which they are given in the question.
Complex Numbers
Numbers that are not real are called imaginary numbers, and are indicated by the notation \(i\). The imaginary unit is equal to the square root of \(-1\), or:
\[i = \pm \sqrt {-1}\]
When imaginary numbers combine with real numbers, they are called complex numbers. Try this question:
Which of the following choices gives the correct value of \(3i^{26}\)?
Before you start with the tedious repeated multiplication (\(26\) times!), let’s get acquainted with this unique property of \(i\): When \(i\) is multiplied by itself (or raised to an exponent), it follows this repetitive \(4\)-point cycle:
\[i^1 = i\] \[i^2 = i \cdot i = \sqrt{-1} \cdot \sqrt{-1} = -1\] \[i^3 = -1 \cdot i = -i\] \[i^4 = -i \cdot i = -\cdot \sqrt{-1} \cdot{-1} = -(-1) = 1\]Then \(i^5 = i\), which starts another cycle which ends with \(i^8 = 1\).
The seemingly difficult sample question above, then, becomes an easy one with this solution:
\[3i^{26} = 3(i^{24} \cdot i^2) = 3 (1 \cdot -1) = -3\]Take note that when we raise \(i\) to a multiple of \(4\), the value will always be equal to \(1\).
Vectors and Matrices
Vectors are values with magnitude and direction. Vectors are written in a row or column. This is a vector:
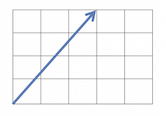
And here is another:
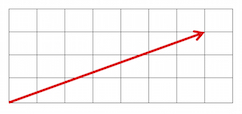
The two vectors can be added to get the resultant vector below:
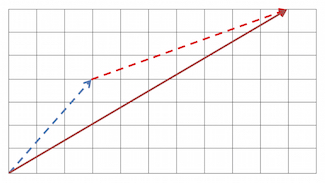
Without the visuals, though, we ought to know now that we add vectors by adding the corresponding elements in the row or column:
\[(3, 4) + (7, 3) = (10, 7)\]Matrices, on the other hand, are an array of values in rows and columns. There can be one or more rows, and one or more columns. So a vector is also a matrix. The determinant is a number computed from a square matrix, such as a \(2\)x\(2\) or a \(3\)x\(3\) matrix.
Vectors, matrices, and determinants are useful in solving systems of equations. A system of linear equations, for example, can be solved using matrices instead of the elimination or substitution methods.
These concepts also find application in calculus, physics, and astronomy. At this level, you are expected to know how to perform the basic operations using vectors and matrices and to calculate the determinant.
Review further about topics such as adding and subtracting matrices, multiplying a matrix by a scalar, multiplying a matrix by another matrix, dividing (or multiplying by an inverse of a matrix), transposing a matrix, and calculating the determinant of a matrix.
Number Theory
The concepts mentioned involving natural numbers and integers are part of the study of numbers, called the Number Theory. Explore the properties of odd and even numbers, primes and composites, and prime factorization. You will find these number properties useful when reasoning out mathematically. Other types of numbers, albeit rarely seen in this test, are perfect, triangular, and Fibonacci numbers.
All Study Guides for the ISEE are now available as downloadable PDFs