Next Generation Quantitative Reasoning, Algebra, and Statistics Study Guide for the ACCUPLACER Test
Page 3
Linear Equations
Linear equations are those that relate a variable to the first power to another variable also raised to the first power. The general form of a linear equation is \(y = mx\), where \(m\) is the slope of the line and \((x, y)\) represent points along the line.
Graphically, linear equations do not curve; they represent straight lines, hence the word “linear”.
Create a Linear Equation
You will encounter many word problems describing linear relationships. It is important to be able to translate the information in these word problems to algebraic expressions and equations. Any scenario that relates one variable to a constant multiplicative change in another variable can be represented with a linear equation.
When reading a word problem, decide which values are unknown and choose variables to represent these unknown values.
Determine what relationship exists between the unknown values and any given values—usually through an operation like multiplication or division. After an equation or set of equations is established, the unknown values can be determined.
If the question provides only a single unknown, only one equation is required to determine the unknown’s value. If the question provides multiple unknowns, as many equations as there are unknowns are required to solve each unknown.
Consider this scenario:
Vi earns \(\$21\) per hour as a cosmetic chemist in addition to a bonus of \(\$300\) per month. Write an equation representing Vi’s total monthly income. How much does Vi earn if she works \(100\) hours in the month?
Let \(M\) represent her total monthly income and \(h\) represent her hourly wage. By multiplying her hourly wage by the number of hours, we compute the total amount earned over those hours. This subtotal is then combined with her bonus to yield her total monthly income:
\[M = 21h + 300\]Substitute \(100\) for \(h\) to determine the total monthly income:
\[M = 21(100) + 300 = 2100 + 300 = 2400\]Notice that if her total monthly income were given, the same equation could be used to determine the number of hours she worked.
Solve a Linear Equation
Linear equations can involve one or multiple variables. Solving a one-variable linear equation entails computing the value of the variable. Solving a two-variable linear equation entails writing one of the variables in terms of the other variable, or vice versa. Linear equations with more than two variables can be solved in the same way as for two-variable equations; that is, they may be solved by writing one variable in terms of the others and substituting it into another equation to eliminate one variable at a time.
The process of solving a single-variable linear equation involves isolating the variable by undoing all of the operations that are performed on it. For example:
\[x + 3 = 9\]Here, \(3\) is added to the variable, so, to isolate the variable undo the addition of \(3\) by subtracting it from both sides (if the \(3\) is only subtracted from one side, the equality will be broken):
\[x = 9 - 3 = 6\]This answer can be verified by substituting the value into the original equation:
\((6) + 3 = 9\), which is a true statement.
Consider this example:
\[\frac{2x + 3}{5} = -2\]To isolate the variable, undo all of the operations performed on it by following the reverse of the order of operations. Begin by multiplying both sides by \(5\) to isolate the \((2x + 3)\):
\[2x + 3 = -10\]Next subtract \(3\) from both sides, then divide both sides by \(2\):
\[x = -\frac{13}{2}\]Substituting this value into the original equation verifies the answer.
Two-variable linear equations follow the same process, but a final value cannot be computed unless more information, such as another linear equation, is given. Consider this example:
\[\frac{4x - 1}{2} + 3y = 4\]Because we have two variables but only one equation, we can only solve for \(x\) in terms of \(y\) or solve for \(y\) in terms of \(x\). Here, we will solve for \(y\):
\[3y = 4 - \frac{4x - 1}{2}\]and dividing both sides by \(3\) and combining terms without the variable \(x\)
\[y = -\frac{2}{3}x + \frac{3}{2}\]which is the equation of a line with a negative slope that passes through the point \((0, \frac{3}{2})\).
Solve a Linear Inequality
Solving linear inequalities is very similar to solving linear equations, with one minor difference. Graphing linear inequalities involves more steps than graphing a linear equation.
When solving an inequality that requires the multiplication or division of a negative value, the direction of the inequality sign switches.
For example:
\(-3x < 9\) is solved as \(x > -3\)
Inequalities involving only “less than” or “greater than” signs do not include the value computed as part of the solution set. This is designated graphically with an open circle in the case of a one-variable inequality, or a dotted line on a coordinate plane, and with a dotted line in the case of a two-variable inequality.
Inequalities involving a “less than or equal to” sign and a “greater than or equal to” sign include the value computed as part of the solution set. This is designated graphically with a closed circle in the case of a one-variable inequality, or a bold line on a coordinate plane, and with a bold line in the case of a two-variable inequality.
In the case of two-variable inequalities, when \(y > x\), the portion above the line (dotted or bold) is shaded in order to indicate the solution set. When \(y < x\), the portion below the line (dotted or bold) is shaded in order to indicate the solution set.
For example, \(x > 3\) is graphed as:

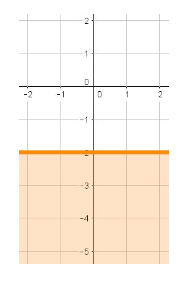
\(y \le -2\) is graphed as:
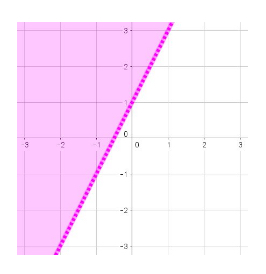
\(y > 2x + 1\) is graphed as:
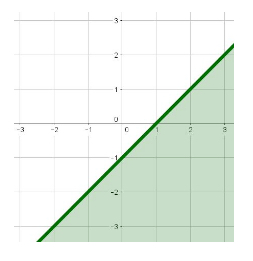
\(y \le x - 1\) is graphed as:
Solve a System of Two Linear Equations
Systems involving two linear equations can be solved using many methods. Many problems you will encounter can be solved using the techniques of substitution, elimination, or graphing.
We will use these three methods to solve the following system:
\(y = \frac{2}{3}x\) and \(y = -x + 5\)
Substitution
The method of substitution involves solving one of the equations for a variable, then substituting the expression for this variable into the other equation to find the numeric value of the variable. After one of the variables is found, its value can be placed into either equation to then find the value of the other variable.
Substitute the expression for \(y\) from the first equation into the second:
\[\frac{2}{3}x = -x + 5\]and adding x to both sides:
\[\frac{5}{3}x = 5\]which gives
\[x = 3\]This value of \(x\) can be substituted into either equation to solve for \(y\):
\[y = \frac{2}{3} \cdot 3\]which gives
\[y = 2\]The solution to the system is \((x, y) = (3, 2)\). Graphically, it represents the point at which the two lines intersect. We started by using the expression for \(y\) in terms of \(x\) from the first equation and substituting it into the second, but we could have arrived at the same result by solving for \(y\) in the second equation and substituting it into the first. We could also have solved for \(x\) in either equation instead. Choosing which variable to solve for and in which equation is simply a matter of preference; you can use whichever you find easier to calculate.
Elimination
The method of elimination involves combining both equations such that one of the variables is eliminated in the process. This is done by adding or subtracting the left side of one equation from the left side of the other and, likewise, the right side of the first equation from the right side of the other.
In the example given, if the second equation is subtracted from the first, the \(y\) variables will disappear, and the \(x\) variable can then be found:
\[y - y = \frac{2}{3}x - (-x + 5)\] \[0 = \frac{2}{3}x + x - 5\] \[5 = \frac{5}{3}x\] \[x = 3\]This value can then be substituted into either equation to solve the system.
Graphing
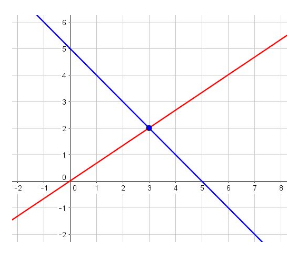
The method of graphing entails graphing each line and finding the point of intersection. The following graph shows the point of intersection, which represents the solution to the system of equations:
All Study Guides for the ACCUPLACER Test are now available as downloadable PDFs