Next Generation Advanced Algebra and Functions Study Guide for the ACCUPLACER Test

Quadratics

As mentioned in a previous section, the general form of a quadratic equation is: \(Ax^2 + Bx + C = 0\).

A quadratic equation graphs as a parabola, with a maximum or minimum value depending on the value of the \(A\) coefficient. The orange curve shows the case where \(A > 0\) and the blue curve shows the case of \(A < 0\):

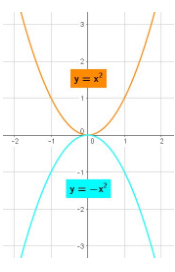
The value of the \(C\) coefficient is the \(y\)-intercept of the parabola (when it is of the form \(y = Ax^2 + Bx + C\).

There are three possible solution sets for a quadratic equation:

• two real solutions
• one real solution
• two imaginary solutions

Algebraically, two real solutions result from a positive discriminant, which is the portion of the quadratic formula within the square root:

\[b^2 - 4ac\]

Graphically, having two real solutions is equivalent to a parabola that passes through the \(x\)-axis at two points.

Recall that the solution to a quadratic equation represents the input values for which the output value is \(0\).

In the second case, the vertex of the parabola is located on the \(x\)-axis and the discriminant is equal to \(0\):

\(b^2 - 4ac = 0\).

In the last case, the discriminant is less than \(0\): \(b^2 - 4ac < 0\), which results in the square root of a negative value. Graphically, this is the case when the parabola does not cross the \(x\)-axis.

Creating

Consider this situation:

The length of a square plot of land is increased by \(4\) units and the width of the same square plot is increased by \(7\) units. The area becomes \(450 \;units^2\). What is the original side length of the square plot?

To solve:

It is given that the original square plot, which has dimensions of \(x\) by \(x\), has its length and width increased. The new length is \(x + 4\), and the new width is \(x + 7\). It is also given that the new area is \(450\) \(units^2\). Substitute the new length and width into the equation for the area of a rectangle:

\((x + 4)(x + 7) = 450\), which becomes

\(x^2 + 11x + 28 = 450\), which becomes

\[x^2 + 11x - 422 = 0\]

This does not factor nicely, so the quadratic formula can be used to solve for the original side length \(x\):

\(x \approx -26.7\) and \(x \approx 15.7\)

Because the variable represents a side length, it cannot be a negative value. So, the only reasonable solution is \(x \approx 15.7\).

When situations can be modeled using a quadratic equation, the solution can be found using the quadratic formula, or any appropriate factoring method.

Solving

Solving a quadratic equation entails finding a value for the variable in question, usually \(x\), that when plugged into the original equation yields a true statement. It is imperative that the technique of factoring is mastered so that equations can be rewritten into a more workable form. Additionally, the quadratic formula must be memorized.

Consider this example:

\[x^2 - 2x - 24 = 0\]

To begin factoring, consider the factors of \(-24\) that sum to \(-2\):

\(-1 + 24 \ne -2\), and
\(-2 + 12 \ne -2\), and
\(-4 + 6 \ne 2\), but
\(-6 + 4 = 2\), so the factors are \(x + 4\) and \(x - 6\).

So the original equation can be rewritten as:

\((x + 4)(x - 6) = 0\), and because the product of anything and \(0\) is \(0\), either expression can be set equal to \(0\) and \(x\) can be found:

\(x + 4 = 0\) and \(x - 6 = 0\), so \(x = -4\), and \(x = 6\)

For equations that cannot be easily factored, the quadratic formula can be used to solve for \(x\). The quadratic formula is:

\(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\), when the equation is written in the form \(ax^2 + bx + c = 0\)

Simplifying

Occasionally a quadratic equation or inequality will be presented which should be simplified before it can be factored. In such cases, arithmetic will be used to simplify where possible and the resulting expression will then be factored.

Consider these examples:

\(\frac{4x^5 + 4x^4 - 12x^3}{4x^3} = 0\) and \(\frac{-5x^3 - 15x^2 + 40x}{5x} \le 12 + x\)

The first equation can be simplified by first factoring out the GCF of \(4x^3\) from the numerator and dividing by \(4x^3\):

\(\frac{4x^3(x^2 + x - 3)}{4x^3} = 0\), which becomes:

\[x^2 + x - 3 = 0\]

which can now be factored using the quadratic formula.

The second equation can also be simplified by first factoring the GCF from the numerator, then dividing by the denominator, then moving the terms on the right side to the left side:

\(\frac{5x(-x^2 - 3x + 8)}{5x} \le 12 + x\), which becomes

\(-x^2 - 3x + 8 \le 12 + x\), and moving the right terms to the left side

\(-x^2 - 2x - 4 \le 0\), which can now be factored using the quadratic formula.

Solving Systems that Include a Quadratic Equation

Systems of equations that contain a linear equation and a quadratic equation have three possible solution set cases.

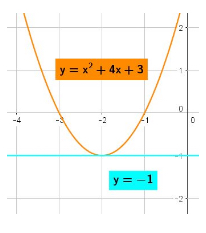
In the first case, the graph of the line and the graph of the quadratic do not intersect, and because there are no points of intersection, the system has no solution:

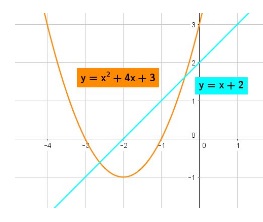
In the second case, the line and the equation intersect at exactly one point. In this case, there is only one solution:

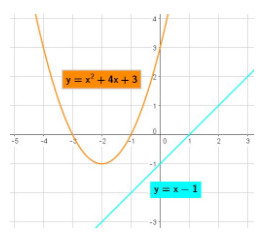
In the third case, the line and the quadratic intersect at two points. In this case, there are two solutions:

We will use the third case presented above as an example for solving the system algebraically. The system is:

\(y = x^2 + 4x + 3\) and \(y = x + 2\)

By setting the expressions equal to each other, we can eliminate one of the variables and then solve using any appropriate method:

\(x^2 + 4x + 3 = x + 2\), and rearranging:

\[x^2 + 3x + 1 = 0\]

This expression does not factor nicely, so it is necessary to use the quadratic formula:

\[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]

You can do the algebra, but the solution set is:

\((-2.62, -0.62)\) and \((-0.38, 1.62)\)

The quadratic formula can be used to solve any quadratic equation.